Pregunta 11. Si 3x-2y=11 y xy = 12, encuentra el valor de 27x 3 -8y 3
Solución:
Dado, 3x-2y=11 y xy=12
sabemos que (ab) 3 = a 3 -b 3 -3ab(ab)
(3x-2y) 3 = 11 3
27x 3 -8y 3 -3(12)(11)=1331
27x 3 -8y 3 =1331+2376
27x 3 -8y 3 =3707
Por lo tanto, el valor de 27x 3 -8y 3 = 3707
Pregunta 12. Si (x 4 +1/x 4 )=119, encuentra el valor de (x 3 -1/x 3 )
Solución:
Dado, (x 4 +1/x 4 ) =119 —— 1
sabemos que (x+y) 2 = x 2 +y 2 +2xy
sustituir el valor dado en eq-1
(x2 + 1/x2 ) 2 = x4 + 1/x4 +2 ( x2 )(1/ x2 )
= x 4 +1/x 4 +2
= 119+2
= 121
(x 2 +1/x 2 ) 2 = ±11
Ahora encuentra (x-1/x)
sabemos que (xy) 2 =x 2 +y 2 -2xy
(x-1/x) 2 = x2 +1/ x2 -2*x*1/x
= x 2 +1/x 2 -2
= 11 -2
= 9
(x-1/x) = ±3
necesitamos encontrar x 3 -1/x 3
sabemos que , a 3 -b 3 =(ab)(a 2 +b 2 -ab)
x 3 -(1/x) 3 =(x-1/x)(x 2 +(1/x) 2 -x*1/x)
Aquí, x 2 +1/x 2 = 11 y x-1/x=3
x3 -1 /x3 = 3(11+1)
= 3(12)
= 36
Por lo tanto, el valor de x 3 -1/x 3 =36
Pregunta 13. Evalúe cada uno de los siguientes:
(a) (103) 3
(b) (98) 3
(c) (9.9) 3
(d) (10.4) 3
(e) (598) 3
(f) (99) 3
Solución:
Dado:
(a) (103) 3
sabemos que (a+b) 3 = a 3 +b 3 +3ab(a+b)
(103) 3 se puede escribir como (100+3) 3
Aquí, a=100 y b=3
(103) 3 = (100+3) 3
=100 3 +3 3 +3(100)(3)(100+3)
=1000000+27+900(103)
=1092727
El valor de (103) 3 =1092727
(b) (98) 3
sabemos que (ab) 3 = a 3 -b 3 -3ab(ab)
(98) 3 = (100-2) 3
= 100 3 -2 3 -3(100)(2)(100-2)
= 1000000-8-600(98)
= 941192
El valor de (98) 3 = 941192
(c) (9.9) 3
sabemos que (ab) 3 = a 3 -b 3 -3ab(ab)
(10-0,1) 3 = (10) 3 -(0,1) 3 -3(10)(0,1)(10-0,1)
= 1000 – 0,001-3(9,9)
= 970.299
El valor de (9.9) 3 =970.299
(d) (10.4) 3
sabemos que (a+b) 3 = a 3 +b 3 +3ab(a+b)
(10+0,4) 3 =(10) 3 +(0,4) 3 +3(10)(0,4)(10+0,4)
= 1000+0.064+12(10.4)
= 1124.864
El valor de (10.4) 3 =1124.864
(e) (598) 3
sabemos que (ab) 3 = a 3 -b 3 -3ab(ab)
(600-2) 3 = (600) 3 -2 3 -3(600)(2)(600-2)
= 216000000 – 8 -(3600*598)
= 216000000 -8 – 2152800
= 213847192
El valor de (598) 3 = 213847192
(f) (99) 3
sabemos que (ab) 3 = a 3 -b 3 -3ab(ab)
(100-1) 3 = (100) 3 -1 3 -3(100)(1)(100-1)
= 1000000 – 1 -300*99
= 1000000 – 1 -29700
= 970299
El valor de (99) 3 = 970299
Pregunta 14. Evalúe cada uno de los siguientes
(a) 111 3 – 89 3
(b) 46 3 +34 3
c) 104 3 +96 3
(d) 93 3 – 107 3
Solución:
Dado:
(a) 111 3 – 89 3
La ecuación anterior se puede escribir como (100+11) 3 – (100-11) 3
sabemos que , (a+b) 3 -(ab) 3 = 2[b 3 +3a 2 b]
Aquí, a=100 b=11
(100+11) 3 – (100-11) 3 = 2[11 3 +3(100) 2 (11)]
= 2[1331 + 330000]
= 2[331331]
= 662662
El valor de 111 3 -89 3 = 662662
(b) 46 3 + 34 3
La ecuación anterior se puede escribir como (40+6) 3 – (40-6) 3
sabemos que , (a+b) 3 +(ab) 3 = 2[a 3 +3ab 2 ]
Aquí, a = 40 y b = 6
(40+6) 3 – (40-6) 3 = 2[(40) 3 +3(6) 2 (40)]
= 2[64000+3*36*40]
=2[68320]
= 136640
El valor de 46 3 +34 3 =136640
c) 104 3 +96 3
La ecuación anterior se puede escribir como (100+4) 3 + (100-4) 3
sabemos que, (a+b) 3 +(ab) 3 = 2[a 3 +3ab 2 ]
aquí, a = 100 , b = 4
(100+4) 3 +(100-4) 3 = 2[(100) 3 +3(100)(4) 2 ]
= 2[1000000 + 300*16]
= 2[1004800]
= 2009600
El valor de 104 3 + 96 3 = 2009600
(d) 93 3 – 107 3
La ecuación anterior se puede escribir como (100-7) 3 – (100+7) 3
sabemos que, (ab) 3 -(a+b) 3 = -2[b 3 +3a 2 b]
aquí, a = 100 , b = 7
(100-7) 3 – (100+7) 3 = -2[7 3 +3*(100) 2 *7]
= -2[210343]
= -420686
El valor de 93 3 – 107 3 = -420686
Pregunta 15. Si x+1/x = 3, calcula x 2 +1/x 2 , x 3 +1/x 3 , x 4 +1/x 4
Solución:
Dado, x+1/x=3
sabemos que (x+y) 2 = x 2 +y 2 +2xy
(x+1/x) 2 = x2 + (1/x) 2 +2x(1/x)
(3) 2 = x2 + (1/x) 2 +2
x 2 + 1/x 2 = 7
cuadratura en ambos lados
(x 2 + 1/x 2 ) 2 = 49
x4 +1/x4 +2 (x2 ) ( 1/x2 ) = 49
x4 +1/ x4 = 49-2
x 4 + 1/x 4 = 47
otra vez al cubo en ambos lados,
(x+1/x) 3 = x3 + 1/ x3 +3*x*1/x(x+1/x)
3 3 = x 3 +1/x 3 +3(3)
x 3 +1/x 3 = 27-9
x 3 + 1/x 3 = 18
El valor x 2 +1/x 2 = 7, x 3 +1/x 3 = 18, x 4 +1/x 4 = 47
Pregunta 16. Si x 4 +1/x 4 =194, calcula x 2 +1/x 2 , x 3 +1/x 3 , x+1/x
Solución:
Dado,
x4 + 1/x4 = 194 —– 1
suma y resta (2*x 2 *1/x 2 ) en el lado izquierdo en la ecuación anterior
x4 +1/ x4 +2* x2 * 1 / x2 -2*x*1/ x2 = 194
x4 +1/ x4 +2* x2 * 1 /x2 -2 =194
(x 2 ) 2 + (1/x 2 ) 2 + 2*x 2 * 1/x 2 = 196
(x 2 + 1/x 2 ) 2 = 196
(x 2 +1/x 2 ) = 14 ——— 2
suma y resta (2*x*1/x) en el lado izquierdo en la ecuación anterior
x2 +1/ x2 +2*x*1/x-2*x*1/x = 14
(x+1/x) 2 = 14 +2
(x+1/x) = 4 ———— 3
Ahora al cubo eq-3 en ambos lados.
(x+1/x) 3 = 4 3
x3 +1/x3 + 3*x*1/x(x+1/x) = 64
x3 +1/x3 + 3*4 = 64
x 3 +1/x 3 = 64 -12
= 52
Por lo tanto, los valores de (x 2 +1/x 2 ) = 14, (x 3 +1/x 3 ) = 52, (x+1/x) = 4
Pregunta 17. Encuentra el valor de 27x 3 +8y 3 , si
(a) 3x+2y=14 y xy = 8
(b) 3x+2y = 20 y xy=14/9
Solución:
(a) Dado, 3x+2y = 14 y xy = 8
al cubo en ambos lados
(3x+2y) 3 = 14 3
sabemos que, (a+b) 3 =a 3 +b 3 +3ab(a+b)
27x 3 +8y 3 +3(3x)(2y)(3x+2y) = 2744
27x 3 +8y 3 +18xy(3x+2y) = 2744
27x 3 +8y 3 +18*8*14 = 2744
27x 3 +8y 3 = 2744 – 2016
27x 3 +8y 3 = 728
Por lo tanto, el valor de 27x 3 +8y 3 = 728
(b) Dado, 3x+2y = 20 y xy=14/9
al cubo en ambos lados
sabemos que, (a+b) 3 =a 3 +b 3 +3ab(a+b)
27x 3 +8y 3 +3(3x)(2y)(3x+2y) = 8000
27x 3 +8y 3 +18xy(3x+2y) = 8000
27x 3 +8y 3 +18*14/9*20 = 8000
27x 3 +8y 3 = 8000 – 560
= 7440
Por lo tanto, el valor de 27x 3 +8y 3 = 7440
Pregunta 18. Encuentra el valor de 64x 3 -125z 3 , si 4x-5z=16 y xz=12
Solución:
Dado, 64x 3 – 125z 3
Aquí, 4x -5z = 16 y xz = 12
al cubo (4x-5z) 3 = 16 3
sabemos que (ab) 3 =a 3 -b 3 -3ab(ab)
(4x -5z) 3 = (4x) 3 -(5z) 3 -3(4x)(5z)(4x-5z)
(16) 3 = 64x 3 -125z 3 -60(4x-5z)
4096 = 64x 3 -125z 3 -60(16)
64x 3 -125z 3 = 4096 + 960
= 5056
Por lo tanto, el valor de 64x 3 – 125z 3 = 5056
Pregunta 19. Si x-1/x = 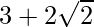 , encuentra el valor de x 3 -1/x 3
, encuentra el valor de x 3 -1/x 3
Solución:
Dado, x-1/x =
al cubo de ambos lados,
sabemos que , (ab) 3 = a 3 -b 3 -3ab(ab)
(x-1/x) 3 = x 3 -1/x 3 -3*x*1/x(x-1/x)
(3+2\raíz cuadrada{2})^3 = x 3 -1/x 3 -3(3
)
x 3 -1/x 3 = 108+
Por lo tanto, el valor de x 3 -1/x 3 = 108+
Publicación traducida automáticamente
Artículo escrito por ranshu1601 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA