Factoriza cada una de las siguientes expresiones:
Pregunta 1. p 3 +27
Solución:
⇒ pag 3 +3 3
⇒(p+3)(p 2 -3p-9) [ a 3 +b 3 =(a+b)(a 2 -ab+b 2 ) ]
Por lo tanto, p 3 +27 = (p+3)(p 2 -3p-9)
Pregunta 2. y 3 +125
Solución:
⇒ y 3 +5 3
⇒ (y+5)(y 2 -3y+25) [ a 3 +b 3 =(a+b)(a 2 -ab+b 2 ) ]
Por lo tanto, y 3 +125 = (y+5)(y 2 -3y+25)
Pregunta 3. 1 – 27a 3
Solución:
⇒ (1) 3 – (3a) 3
⇒ (1-3a)(1 2 +3a+(3a) 2 ) [ a 3 -b 3 =(ab)(a 2 +ab+b 2 ) ]
⇒ (1-3a)(1+3a+9a 2 )
Por lo tanto, 1 – 27a 3 = (1-3a)(1+3a+9a 2 )
Pregunta 4. 8x 3 y 3 +27a 3
Solución:
⇒ (2xy) 3 + (3a) 3
⇒ (2xy+3a)((2xy) 2 -2xy *3a +(3a) 2 ) [ a 3 +b 3 =(a+b)(a 2 -ab+b 2 ) ]
⇒ (2xy+3a)(4x 2 y 2 -6xya +9a 2 )
Por lo tanto, 8x 3 y 3 +27a 3 = (2xy+3a)(4x 2 y 2 -6xya +9a 2 )
Pregunta 5. 64a 3 – b 3
Solución:
⇒ (4a) 3 – b 3
⇒ (4a – b ) ((4a) 2 – 4a*b + b 2 ) [ a 3 -b 3 =(ab)(a 2 +ab+b 2 ) ]
⇒ (4a – b ) (16a 2 – 4a*b + b 2 )
Por lo tanto, 64a 3 – b 3 = (4a – b ) (16a 2 – 4a*b + b 2 )
Pregunta 6. 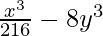
Solución:
⇒
⇒
[ a 3 -b 3 =(ab)(a 2 +ab+b 2 ) ]
⇒
Por lo tanto,
Pregunta 7. 10x 4 y – 10xy 4
Solución:
⇒ 10xy(x 3 -y 3 )
⇒ 10xy(xy)(x 2 +xy+y 2 ) [ a 3 -b 3 =(ab)(a 2 +ab+b 2 ) ]
Por lo tanto, 10x 4 y – 10xy 4 = 10xy(xy)(x 2 +xy+y 2 )
Pregunta 8. 54x 6 y+2x 3 y 4
Solución:
⇒ 2x 3 y(27x 3 +y 3 )
⇒ 2x 3 y((3x) 3 +y 3 ) [ a 3 +b 3 =(a+b)(a 2 -ab+b 2 ) ]
⇒ 2x 3 y(3x+y)(9x 2 -3xy+y 2 )
Por lo tanto, 54x 6 y+2x 3 y 4 = 2x 3 y(3x+y)(9x 2 -3xy+y 2 )
Pregunta 9. 32a 3 +108b 3
Solución:
⇒ 4(8a 3 +27b 3 )
⇒ 4((2a) 3 +(3b) 3 )
⇒ 4 [ (2a+3b) ((2a) 2 -6ab+(3b) 2 )] [ a 3 +b 3 =(a+b)(a 2 -ab+b 2 ) ]
⇒ 4(2a+3b)(4a 2 -6ab +3b 2 )
Por lo tanto, 32a 3 +108b 3 = 4(2a+3b)(4a 2 -6ab +3b 2 )
Pregunta 10. (a-2b) 3 -512b 3
Solución:
⇒ (a-2b) 3 – (8b) 3
⇒ (a-2b-8b)((a-2b) 2 – (a-2b)8b + (8b) 2 ) [ a 3 -b 3 =(ab)(a 2 +ab+b 2 ) ]
⇒ (a – 10b)(a 2 +4b 2 -2ab +8ab + 16b 2 +64b 2 )
⇒ (a – 10b)(a 2 +52b 2 +4ab)
Por lo tanto, (a-2b) 3 -512b 3 = (a – 10b)(a 2 +52b 2 +4ab)
Pregunta 11. (a+b) 3 -8(ab) 3
Solución:
⇒ (a+b) 3 -[2(ab)] 3
⇒ (a+b) 3 – (2a -2b) 3
⇒ [a+b-(2a-2b)]((a+b) 2 +(a+b)(2a-2b)+(2a-2b) 2 [a 3 -b 3 =(ab)(a 2 +ab+b 2 ) ]
⇒ (3b-a)[(a 2 +b 2 +2ab) +(2a 2 -2ab+2ab-2b 2 )+(4a 2 +4b 2 +8ab)]
⇒ (3b-a) [7a 2 +3b 2 -6ab]
Por lo tanto, (a+b) 3 -8(ab) 3 = (3b-a) [7a 2 +3b 2 -6ab]
Pregunta 12. (x+2) 3 (x-2) 3
Solución:
⇒ (x+2+x-2)((x+2) 2 – (x+2)(x-2)+(x-2) 2 )
⇒ 2x(x 2 +4x+4-(x+2)(x-2)+x 2 -4x+4) [(a+b)(ab)=a 2 -b 2 ]
⇒2x(2x 2 +8-(x 2 -2 2 ))
⇒ 2x(x2 + 8+4)
⇒ 2x(x2 + 12)
Por lo tanto, (x+2) 3 (x-2) 3 = 2x(x 2 +12)
Publicación traducida automáticamente
Artículo escrito por ranshu1601 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA