En cada uno de los siguientes usando el teorema del resto, encuentre el recordatorio cuando f(x) se divide por g(x) y verifique por división real: (1-8)
Pregunta 1. f(x) = x 3 +4x 2 -3x+10, g(x) = x+4
Solución:
Dado:f(x)=x 3 +4x 2 -3x+10, g(x)=x+4
de, el teorema del resto cuando f(x) se divide por g(x) =x-(-4) el resto será igual a f(-4).
Sea, g(x)=0
⇒x+4=0
⇒ x = -4
Sustituye el valor de x en f(x)
f(-4)=(-4) 3 +4(-4) 2 -3(-4)+10
= -64+(4*16)+12+10
= -64 +64 +12+10
= 22
Por lo tanto, el resto es 22.
Pregunta 2. f(x)=4x 4 -3x 3 -2x 2 +x-7, g(x) =x-1
Solución:
Dado:f(x)= 4x 4 -3x 3 -2x 2 +x-7, g(x)=x-1
de, el teorema del resto cuando f(x) se divide por g(x) = x-(1) el resto será igual a f(1)
Sea, g(x)=0
⇒x-1=0
⇒x=1
Sustituye el valor de x en f(x)
f(1)= 4(1) 4 -3(1) 3 -2(1) 2 +1-7
= 4-3-2+1-7
= 5-12
= -7
Por lo tanto, el recordatorio es 7.
Pregunta 3. f(x)=2x 4 -6x 3 +2x 2 -x+2, g(x)=x+2
Solución:
Dado: f(x)=2x 4 -6x 3 +2x 2 -x+2, g(x)=x+2
de, el teorema del resto cuando f(x) se divide por g(x) = x-(-2) el resto será igual a f(-2)
Sea, g(x)=0
⇒x+2=0
⇒x=-2
Sustituye el valor de x en f(x)
f(-2)=2(-2) 4 -6(-2) 3 +2(-2) 2 -(-2)+2
= (2*16)-(6*(-8))+(2*4)+2+2
= 32+48+8+2+2
= 92
Por lo tanto, el recordatorio es 92.
Pregunta 4. f(x)=4x 3 -12x 2 +14x-3, g(x)=2x-1
Solución:
Dado:f(x)=4x 3 -12x 2 +14x-3, g(x)=2x-1
de, el teorema del resto cuando f(x) se divide por g(x) = 2(x-1/2) el resto será igual a f(1\2)
Sea, g(x)=0
⇒ 2x-1=0
⇒x=-1/2
Sustituye el valor de x en f(x)
=
=
=
=
Por lo tanto, el recordatorio es
Pregunta 5. f(x)=x 3 -6x 2 +2x-4, g(x)=1-2x
Solución:
Dado:f(x)=x 3 -6x 2 +2x-4, g(x)=1-2x
de, el teorema del resto cuando f(x) se divide por g(x) = -2(x-1/2) el resto será igual a f(1\2)
Sea, g(x)=0
⇒ 1-2x=0
⇒x=1/2
sustituir el valor de x en f(x)
=
=
=
Tomando MCM
=
=
=
Por lo tanto, el resto es
Pregunta 6. f(x)=x 4 -3x 2 +4, g(x)=x-2
Solución:
Dado:f(x)=x 4 -3x 2 +4, g(x)=x-2
de, el teorema del resto cuando f(x) se divide por g(x) = x-(2) el resto será igual a f(2)
Sea, g(x)=0
⇒x-2=0
⇒x=2
Sustituye el valor de x en f(x)
f(2)=2 4 -3(2) 2 +4
= 16-3(4) + 4
= 16 – 12 + 4
= 20 – 12
= 8
Por lo tanto, el resto es 8
Pregunta 7. f(x)=9x 3 -3x 2 +x-5, g(x)=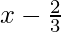
Solución:
Dado:f(x)=9x 3 -3x 2 +x-5, g(x)=
de, el teorema del resto cuando f(x) se divide por g(x) = x-(
) el resto será igual a f(
)
Sea, g(x)=0
⇒x-2/3=0
⇒x=2/3
sustituir el valor de x en f(x)
=
=
=
= -3
Por lo tanto, el resto es -3
Pregunta 8. f(x) = 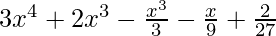 , g(x) =
, g(x) =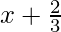
Solución:
Dado:
,
de, el teorema del resto cuando f(x) se divide por g(x) = x-(-\frac23) el resto será igual a f(
)
sustituir el valor de x en f(x)
=
=
= 0
Por lo tanto, el resto es 0
Pregunta 9. Si el polinomio 2x 3 +ax 2 +3x-5 yx 3 +x 2 -4x+a deja el mismo recordatorio cuando se divide por x-2, Encuentra el valor de a .
Solución:
Dado:f(x)=2x 3 +ax 2 +3x-5,p(x)=x 3 +x 2 -4x+a
El resto son f(2) y p(2) cuando f(x) y p(x) se dividen por x-2
Lo sabemos,
f(2) = p(2) (dado en el problema)
necesitamos calcular f(2) y p(2)
para, f(2)
sustituir (x=2) en f(x)
f(2)=2(2) 3 +a(2) 2 +3(2)-5
= 16+4a+1
= 4a+17 ———- 1
para, p(2)
Sustituye (x=2) en p(x)
p(2)=2 3 +2 2 -4(2)+a
= 8+4-8+a
= 4+a ———– 2
Ya que, f(2) = p(2)
Igualar eq1 y eq2
⇒ 4a+17 = 4+a
⇒ 3a = -13
⇒ a = -13/3
El valor de a = -13/3
Pregunta 10. Si los polinomiosax 3 +3x 2 -3 y 2x 3 -5x+a cuando se dividen por (x-4) dejan los recordatorios como R1 y R2 respectivamente. Encuentre los valores de a en cada uno de los siguientes casos, si
1. R1 = R2
2.R1+R2=0
3. 2R1-R2=0
Solución:
Los polinomios son f(x)=ax 3 +3x 2 -3,p(x)=2x 3 -5x+a
dejar,
R1 es el recordatorio cuando f(x) se divide por x-4
⇒ R1=f(4)
⇒ R1=a(4) 3 + 3(4) 2 -3
= 64a + 48 – 3
= 64a + 45 —————– 1
Ahora deja
R2 es el recordatorio cuando p(x) se divide por x-4
⇒ R2=p(4)
⇒ R2=2(4) 3 -5(4)+a
= 128-20+a
= 108 +a ——————— 2
1. Dado, R1 = R2
⇒ 64a + 45 = 108 +a
⇒ 63a=63
⇒ un =1
2. Dado, R1+R2 =0
⇒ 64a + 45 + 108 +a = 0
⇒ 65a + 153 = 0
⇒ a = -153/65
3. Dado, 2R1-R2 =0
⇒2( 64a + 45)- (108 +a) =0
⇒ 128a + 90 – 108 -a =0
⇒ 127a – 18 =0
⇒ un =
Pregunta 11. Si los polinomiosax 3 +3x 2 -13 y 2x 3 -5x+a cuando se dividen por (x-2) dejan el mismo recordatorio, encuentra el valor de a.
Solución:
Dado:f(x)=ax 3 +3x 2 -13,p(x)=2x 3 -5x+a
Igualar x-2 a cero
⇒x=2
Sustituye el valor de x en f(x) y p(x)
f(2)=a(2) 3 +3(2) 2 -13
= 8a+12-13
= 8a-1 ————– 1
p(2)=2(2) 3 -5(2)+a
= 16-10+a
= 6 + a ————- 2
f(2) = p(2)
⇒ 8a-1 = 6+a
⇒ 7a = 7
⇒ un =1
el valor de a es 1
Pregunta 12. Encuentra el recordatorio cuando f(x)=(x) 3 +3(x) 2 +3(x)+1 se divide por,
1. x+1
2. x – 1/2
3. x
4. x+π
5. 5+2x
Solución:
Dado:f(x)=x 3 +3x 2 +3x+1
por el teorema del recordatorio
1.x+ 1 = 0
x=-1
Sustituye el valor de x en f(x)
f(-1)=(-1) 3 +3(-1) 2 +3(-1)+1
= -1+3-3+1
=0
2. x-1/2 =0
X = 1/2
Sustituye el valor de x en f(x)
=
=
=
3. x = 0
Sustituye el valor de x en f(x)
f(0)=(0) 3 +3(0) 2 +3(0)+1
= 0 + 0+0+1
= 1
4. x+π =0
x = -π
Sustituye el valor de x en f(x)
f(-π)=(-π) 3 +3(-π) 2 +3(-π)+1
=-π 3 +3π 2 -3π +1
5. 5+2x =0
x = -5/2
Sustituye el valor de x en f(x)
=
Tomando MCM
=
=
Publicación traducida automáticamente
Artículo escrito por ranshu1601 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA