Pregunta 13. Encuentra el valor de k si x – 3 es un factor de k 2 x 3 – kx 2 + 3kx – k
Solución:
Sea, f(x) = k 2 x 3 – kx 2 + 3kx – k
Según el teorema del factor
Si x – 3 es el factor de f(x), entonces f(3) = 0
⇒ x – 3 = 0
⇒ x = 3
Al sustituir el valor de x en f(x), obtenemos
f(3) = k 2 (3) 3 – k(3) 2 + 3k(3) – k
= 27k 2 – 9k + 9k – k
= 27k 2 – k
= k( 27k – 1)
Igualar f(3) a cero, para encontrar k
⇒ f(3) = 0
⇒ k(27k – 1) = 0
⇒ k = 0 y 27k – 1 = 0
⇒ k = 0 y k = 1/27
Cuando k = 0 y 1/27, (x – 3) será el factor de f(x)
Pregunta 14. Encuentra el valor de a y b, si x 2 – 4 es un factor de f(x) = ax 4 + 2x 3 – 3x 2 + bx – 4
Solución:
Dado: f(x) = ax 4 + 2x 3 – 3x 2 + bx – 4, g(x) = x 2 – 4
Necesitamos encontrar los factores de g(x)
⇒ x 2 – 4 = 0
⇒x2 = 4
⇒ x = √4
⇒x = ±2
(x – 2) y (x + 2) son los factores
Según el teorema del factor
Si (x – 2) y (x + 2) son los factores de f(x)
el resultado de f(2) y f(-2) debe ser cero
Sea, x – 2 = 0
⇒ x = 2
Al sustituir el valor de x en f(x), obtenemos
f(2) = a(2) 4 + 2(2) 3 – 3(2) 2 + b(2) – 4
= 16a + 2(8) – 3(4) + 2b – 4
= 16a + 2b + 16 – 12 – 4
= 16a + 2b
Igualar el valor de f(2) a cero
⇒ 16a + 2b = 0
⇒ 2(8a + b) = 0
⇒ 8a + b = 0 -(1)
Sea, x + 2 = 0
x = -2
Al sustituir el valor de x en f(x), obtenemos
f(-2) = a(-2) 4 + 2(-2) 3 – 3(-2) 2 + b(-2) – 4
= 16a + 2(-8) – 3(4) – 2b – 4
= 16a – 16 – 12 – 2b – 4
= 16a – 2b – 32
Igualar el valor de f(-2) a cero
⇒ 16a – 2b – 32 = 0
⇒ 16a – 2b – 32 = 0
⇒ 8a – b = 16 -(2)
Al resolver la ecuación (1) y (2)
8a + b = 0
8a – b = 16
16a = 16
un = 1
Al sustituir el valor de a en la ecuación (1), obtenemos
8(1) + b = 0
b = -8
Los valores son a = 1 y b = -8
Pregunta 15. Encuentra 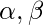 si (x + 1) y (x + 2) son factores de
si (x + 1) y (x + 2) son factores de 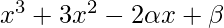
Solución:
Dado:
y los factores son (x + 1) y (x + 2)
Según el teorema del factor,
Si son los factores de f(x), entonces los resultados de f(-2) y f(-1) deberían ser cero.
Dejar,
⇒ x + 1 = 0
⇒ x = -1
Al sustituir el valor de x en f(x), obtenemos
=
=
= 2\alfa +\beta +2 -(1)
Dejar,
⇒ x + 2 = 0
⇒ x = -2
Al sustituir el valor de x en f(x), obtenemos
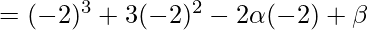
=
-(2)
Al resolver la ecuación (1) y (2)
⇒
⇒
⇒
⇒
Al sustituir
en la ecuación (1)
⇒
⇒
⇒
Los valores son
y
Pregunta 16. Encuentra los valores de p y q para que x 4 + px 3 + 2x 2 – 3x + q sea divisible por x 2 – 1
Solución:
Dado: f(x) = x 4 + px 3 + 2x 2 – 3x + q, g(x) = x 2 – 1
Primero, necesitamos encontrar los factores de x 2 – 1
⇒ x 2 – 1 = 0
⇒x2 = 1
⇒x = ±1
⇒ (x + 1) y (x – 1)
Según el teorema del factor
Si x = 1, -1 son los factores de f(x) entonces f(1) = 0 y f(-1) = 0
Tomemos x + 1 = 0
x = -1
Al sustituir el valor de x en f(x), obtenemos
f(-1) = (-1) 4 + p(-1) 3 + 2(-1) 2 – 3(-1) + q
= 1 – p + 2 + 3 + q
= -p + q + 6 -(1)
Tomemos, x – 1 = 0
X = 1
Al sustituir el valor de x en f(x), obtenemos
f(1) = (1) 4 + p(1) 3 + 2(1) 2 – 3(1) + q
= 1 + p + 2 – 3 + q
= p + q -(2)
Al resolver las ecuaciones (1) y (2), obtenemos
-p + q = -6
p + q = 0
2q = -6
q = -3
Al sustituir el valor de q en la ecuación (2), obtenemos
p + q = 0
pag-3 = 0
p = 3
El valor de p = 3 y q = -3
Pregunta 17. Encuentra los valores de a y b para que (x + 1) y (x – 1) sean los factores de x 4 + ax 3 – 3x 2 + 2x + b
Solución:
Dado: f(x) = x 4 + ax 3 – 3x 2 + 2x + b
Los factores son (x + 1) y (x – 1)
Según el teorema del factor
Si x = 1, -1 son los factores de f(x) entonces f(1) = 0 y f(-1) = 0
Tomemos x + 1
⇒ x + 1 = 0
⇒ x = -1
Al sustituir el valor de x en f(x), obtenemos
f(-1) = (-1) 4 + a(-1) 3 – 3(-1) 2 + 2(-1) + b
= 1 – un – 3 – 2 + segundo
= -a + b – 4 -(1)
Tomemos x – 1
⇒ x – 1 = 0
⇒ x = 1
Al sustituir el valor de x en f(x), obtenemos
f(1) = (1) 4 + a(1) 3 – 3(1) 2 + 2(1) + b
= 1 + un – 3 + 2 + segundo
= a + b -(2)
Al resolver la ecuación (1) y (2)
-a + b = 4
a + b = 0
2b = 4
segundo = 2
Al sustituir el valor de b en la ecuación (2), obtenemos
un + 2 = 0
un = -2
Los valores son a = -2 y b = 2
Pregunta 18. Si x 3 + ax 2 – bx + 10 es divisible por x 3 – 3x + 2, encuentra los valores de a y b
Solución:
Dado: f(x) = x 3 + ax 2 – bx + 10, g(x) = x 3 – 3x + 2
Primero necesitamos encontrar los factores de g(x)
g(x) = x3 – 3x + 2
=x 3 – 2x – x + 2
= x(x-2)-1(x-2)
= (x – 1)(x – 2) son los factores
Tomemos (x – 1)
⇒ x – 1 = 0
⇒ x = 1
Al sustituir el valor de x en f(x), obtenemos
f(1) = 1 3 + a(1) 2 – b(1) + 10
= 1 + a – b + 10
= a – b +11 -(1)
Tomemos (x – 2)
⇒ x – 2 = 0
⇒ x = 2
Al sustituir el valor de x en f(x), obtenemos
f(2) = 2 3 + a(2) 2 – b(2) + 10
= 8 + 4a – 2b + 10
= 4a – 2b + 18
Igualando f(2) a cero
⇒ 4a – 2b +18 = 0
⇒ 2a – b + 9 = 0 -(2)
Al resolver las ecuaciones (1) y (2), obtenemos
a – b = -11
2a – b = -9
un = 2
Al sustituir el valor de a en la ecuación (1), obtenemos
⇒ 2 – segundo = – 11
⇒ -b = -11 – 2
⇒ segundo = 13
El valor es a = 2 y b = 13
Pregunta 19. Si tanto (x + 1) como (x – 1) son los factores de ax 3 + x 2 – 2x + b, encuentra los valores de a y b
Solución:
Dado: f(x) = ax 3 + x 2 – 2x + b, (x + 1) y (x – 1) son los factores
Según el teorema del factor,
Si x = -1 y 1 son factores de f(x), entonces f(1) = 0 y f(-1) = 0
Sea, x – 1 = 0
⇒ x = 1
Al sustituir el valor de x en f(x), obtenemos
f(1) = a(1) 3 + (1) 2 – 2(1) + b
= un +1 – 2 + segundo
= a + b – 1 -(1)
Sea, x + 1 = 0
⇒ x = -1
Al sustituir el valor de x en f(x), obtenemos
f(-1) = a(-1) 3 + (-1) 2 – 2(-1) + b
= -a + 1 + 2 + b
= -a + b + 3 -(2)
Al resolver la ecuación (1) y (2), obtenemos
⇒ a + b = 1
⇒ -a + b = -3
⇒ 2b = -2
⇒ b = -1
Al sustituir la b en la ecuación (1)
⇒ un – 1 = 1
⇒ un = 2
Los valores son a = 2 y b = -1
Pregunta 20. ¿Qué se debe sumar a x 3 – 3x 2 – 12x + 19 para que el resultado sea exactamente divisible por x 2 + x – 6
Solución:
Dado: p(x) = x 3 – 3x 2 – 12x + 19, g(x) = x 2 + x – 6
Según el algoritmo de división cuando p(x) se divide por g(x),
el resto será la expresión lineal en x
Sea, r(x) = ax + b se suma a p(x)
⇒ f(x) = p(x) + r(x)
= f(x) = x 3 – 3x 2 – 12x + 19 + hacha + b
Sabemos que, g(x) = x 2 + x – 6
Primero, encontramos los factores de g(x)
⇒ g(x) = x2 + x – 6
= x 2 + 3x – 2x – 6
= x(x+3) – 2(x+3)
= (x – 2)(x + 3)
Según el teorema del factor
Si (x – 2) & (x + 3) son factores de f(x) entonces f(-3) = 0 y f(2) = 0
Sea, x + 3 = 0
⇒ x = -3
Al sustituir el valor de x en f(x), obtenemos
f(-3) = (-3) 3 – 3(-3) 2 – 12(-3) + 19 + a(-3) + b
= -27 – 27 – 3a + 24 + 19 + b
= -3a + b +1 -(1)
Sea, x – 2 = 0
⇒ x = 2
Al sustituir el valor de x en f(x), obtenemos
f(2) = (2) 3 – 3(2) 2 – 12(2) + 19 + a(2) + b
= 8 – 12 + 2a – 24 + b
= 2a + b – 9 -(2)
Al resolver la ecuación (1) y la ecuación (2), obtenemos
⇒ -3a + b = -1
⇒ 2a + b = 9
⇒ -5a = -10
⇒ un = 2
Al sustituir el valor de a en la ecuación (1)
⇒ -3(2) + b = -1
⇒ -6 + b = -1
⇒ segundo = 5
Por lo tanto, r(x) = ax + b
= 2x + 5
Por lo tanto, x 3 – 3x 2 – 12x + 19 es divisible por x 2 + x – 6 cuando se le suma 2x + 5.
Pregunta 21. ¿Qué se debe sumar a x 3 – 6x 2 – 15x + 80 para que el resultado sea exactamente divisible por x 2 + x – 12
Solución:
Sea p(x) = x 3 – 6x 2 – 15x + 80, q(x) = x 2 + x – 12
Según el algoritmo, cuando p(x) se divide por q(x), el resto es una expresión lineal en x.
Entonces, supongamos que r(x) = ax + b se resta de p(x), de modo que p(x) – q(x) es divisible por q(x)
Sea, f(x) = p(x) – q(x)
q(x) = x2 + x – 12
= x 2 + 4x – 3x – 12
= x(x+4) – 3(x+4)
=(x – 3)(x + 4)
Claramente, (x – 3) y (x + 4) son factores de q(x)
Entonces, f(x) es divisible por q(x) si (x – 3) y (x + 4) son factores de q(x)
Según el teorema del factor
f(-4) = 0 y f(3) = 0
⇒ f(3) = 3 3 – 6(3) 2 – 3(a + 15) + 80 – b = 0
= 27 – 54 – 3a – 45 + 80 – b
= -3a – b + 8 -(1)
Similarmente,
f(-4) = 0
f(-4) = (-4) 3 – 6(-4) 2 – 4(a + 15) + 80 – b
⇒ -64 – 96 – 4a + 60 + 80 – b = 0
⇒ 4a – b – 20 = 0
Al restar la ecuación (1) y la ecuación (2), obtenemos
4a – b – 20 = 0 -(2)
⇒ 7a – 28 = 0
⇒ un = 28/7
⇒ un = 4
Al poner a = 4 en la ecuación (1), obtenemos
⇒ -3(4) – b = -8
⇒ -b – 12 = -8
⇒ -b = -8 + 12
⇒ segundo = -4
Al sustituir los valores de a y b en r(x)
⇒ r(x) = hacha + b
⇒ 4x – 4
Por lo tanto, p(x) es divisible por q(x), si se le resta r(x) = 4x – 4.
Pregunta 22. ¿Qué se debe sumar a 3x 3 + x 2 – 22x + 9 para que el resultado sea exactamente divisible por 3x 2 + 7x – 6
Solución:
Sea p(x) = 3x 3 + x 2 – 22x + 9 y q(x) = 3x 2 + 7x – 6
Según el teorema del divisible, cuando p(x) se divide por q(x), el recordatorio es una ecuación lineal en x.
Sea, r(x) = ax + b se suma a p(x), de modo que p(x) + r(x) es divisible por q(x)
f(x) = p(x) + r(x)
⇒ f(x) = 3x 3 + x 2 – 22x + 9(ax + b)
= 3×3 + x2 + x(a – 22) + b + 9
Lo sabemos,
q(x) = 3x 2 + 7x – 6
= 3x 2 + 9x – 2x – 6
= 3x(x+3) – 2(x+3)
= (3x – 2)(x + 3)
Entonces, f(x) es divisible por q(x) si (3x – 2) y (x + 3) son los factores de f(x)
Del teorema del factor
f(2/3) = 0 y f(-3) = 0
Sea, 3x – 2 = 0
3x = 2
X = 2/3
=
=
=
igualar a cero
⇒
⇒ 6a + 9b – 39 = 0
⇒ 2a + 3b – 13 = 0 -(1)
Similarmente,
Sea, x + 3 = 0
⇒ x = -3
f(-3) = 3(-3) 3 + (-3) 2 – 3(a – 22) + b + 9
= -81 + 9 – 3a + 66 + b + 9
= -3a + b + 3
igualar a cero
⇒ -3a + b + 3 = 0
Multiplica la ecuación dada por 3
⇒ -9a + 3b + 9 = 0 -(2)
Al restar la ecuación (1) de la ecuación (2)
⇒ -9a + 3b + 9 – 2a – 3b + 13 = 0
⇒-11a + 22 = 0
⇒-11a = -22
⇒ un = 2
Sobre la sustitución del valor de a en la ecuación (1)
⇒ -3(2) + b = -3
⇒ -6 + b = -3
⇒ segundo = 3
Pon los valores en r(x)
r(x) = hacha + b
= 2x + 3
Por tanto, p(x) es divisible por q(x), si se le suma r(x) = 2x + 3.
Pregunta 23. Si x – 2 es un factor de cada uno de los siguientes dos polinomios, encuentre el valor de a en cada caso:
(i) x 3 – 2ax 2 + ax – 1
(ii) x 5 – 3x 4 – ax 3 + 3ax 2 + 2ax + 4
Solución:
(i) Sea f(x) = x 3 – 2ax 2 + ax – 1
Según el teorema del factor
Si (x-2) es un factor de f(x) entonces f(2) = 0
Sea, x – 2 = 0
⇒ x = 2
Al sustituir el valor de x en f(x), obtenemos
f(2) = 2 3 – 2a(2) 2 + a(2) – 1
= 8 – 8a + 2a – 1
= -6a + 7
Igualar f(2) a cero
⇒ -6a + 7 = 0
⇒ -6a = -7
⇒ un = 7/6
Entonces, (x – 2) es el factor de f(x)
(ii) Sea f(x) = x 5 – 3x 4 – ax 3 + 3ax 2 + 2ax + 4
Según el teorema del factor
Si (x – 2) es un factor de f(x) entonces f(2) = 0
Sea, x – 2 = 0
⇒ x = 2
Al sustituir el valor de x en f(x), obtenemos
f(2) = 2 5 – 3(2) 4 – a(2) 3 + 3a(2) 2 + 2a(2) + 4
= 32 – 48 – 8a + 12 + 4a + 4
= 8a -12
Igualar f(2) a cero
⇒ 8a – 12 = 0
⇒ a = 12/8
⇒ un = 3/2
Entonces, (x – 2) es un factor de f(x)
Pregunta 24. En cada uno de los siguientes dos polinomios, encuentra el valor de a, si (x – a) es un factor:
(i) x 6 – eje 5 + x 4 – eje 3 + 3x – a + 2
(ii) x 5 – a 2 x 3 + 2x + a + 1
Solución:
(i) Sea, f(x) = x 6 – ax 5 + x 4 – ax 3 + 3x – a + 2
Aquí, x – a = 0
⇒ x = un
Al sustituir el valor de x en f(x), obtenemos
f(a) = a 6 – a(a) 5 + (a) 4 – a(a) 3 + 3(a) – a + 2
= un 6 – un 6 + un 4 – un 4 + 3a – un + 2
= 2a+2
igualar a cero
⇒ 2a + 2 = 0
⇒ 2(un + 1) = 0
⇒ un = -1
Entonces, (x – a) es un factor de f(x)
(ii) Sea, f(x) = x 5 – a 2 x 3 + 2x + a + 1
Aquí, x – a = 0
⇒ x = un
Al sustituir el valor de x en f(x), obtenemos
f(a) = a 5 – a 2 (a) 3 + 2(a) + a + 1
= un 5 – un 5 + 2a + un + 1
= 3a + 1
igualar a cero
⇒ 3a + 1 = 0
⇒ 3a = -1
⇒ a = -1/3
Entonces, (x – a) es un factor de f(x)
Pregunta 25. En cada uno de los siguientes dos polinomios, encuentra el valor de a, si (x + a) es un factor:
(i) x 3 + ax 2 – 2x + a +4
(ii) x 4 – a 2 x 2 + 3x – a
Solución:
(i) Sea, f(x) = x 3 + ax 2 – 2x + a + 4
Aquí, x + a = 0
⇒ x = – un
Al sustituir el valor de x en f(x), obtenemos
f(-a) = (-a) 3 + a(-a) 2 – 2(-a) + a + 4
= 3a + 4
igualar a cero
⇒ 3a + 4 = 0
⇒ 3a = -4
⇒ a = -4/3
Entonces, (x + a) es un factor de f(x)
(ii) Sea, f(x) = x 4 – a 2 x 2 + 3x – a
Aquí, x + a = 0
⇒ x = -a
Al sustituir el valor de x en f(x), obtenemos
f(-a) = (-a) 4 – un 2 (-a) 2 + 3(-a) – un
= un 4 – un 4 – 3a – un
= -4a
igualar a cero
⇒ -4a = 0
⇒ un = 0
Entonces, (x + a) es un factor de f(x)
Publicación traducida automáticamente
Artículo escrito por ranshu1601 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA