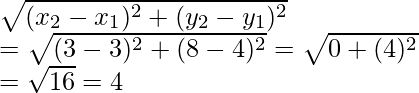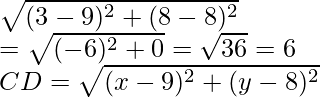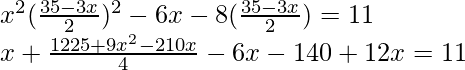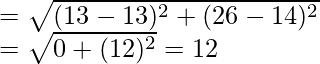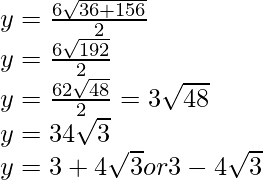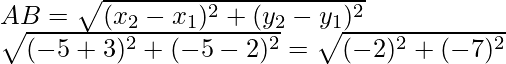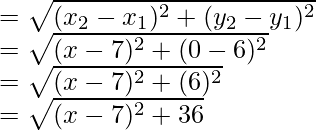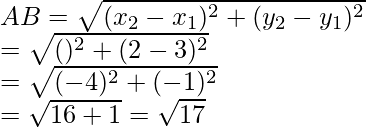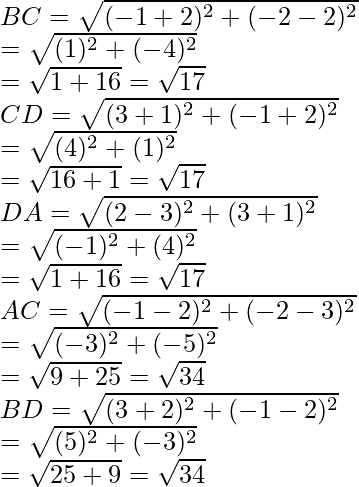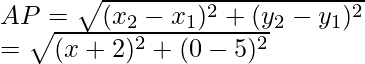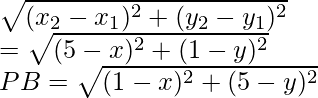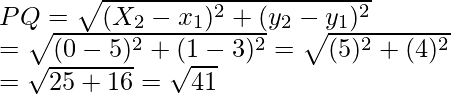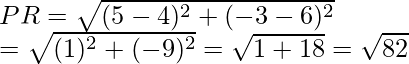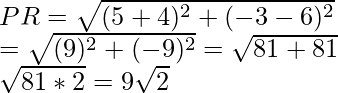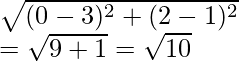Pregunta 20. Los tres vértices de un paralelogramo son (3, 4), (3, 8) y (9, 8). Encuentra el cuarto vértice.
Solución:

Sea ABCD un paralelogramo y los vértices serán A (3, 4), B (3, 8), C (9, 8)
y las coordenadas del cuarto vértice D ser(x, y)
Ahora AB =
Del mismo modo, BC =
y DA =
Por lo tanto, ABCD es un ||gm
Aquí, AB = CD y BC = AD
CD =
Al elevar al cuadrado ambos lados obtenemos
(x – 9) 2 + (y – 8) 2 = (4) 2
x2 – 18x + 81 + y2 – 16y + 64 = 16
x2 + y2 – 18x – 16y = 16 – 81 – 64
x2 + y2 – 18x – 16y = -129 ………..(i)
Del mismo modo, AD =
Al elevar al cuadrado ambos lados obtenemos
(3 – x) 2 + (4 – y) 2 = 26
9 + x2 – 6x + 16 + y2 – 8y = 36
x2 + y2 – 6x – 8y = 36 – 9 – 16
x2 + y2 – 6x – 8y = 11 ………..(ii)
Ahora, al restar la ecuación (i) de (ii), obtenemos
12x + 8y = 140
3x + 2y = 35
2y = 35 – 3x
y = (35 – 3x)/2 ………..(iii)
Ahora sustituyendo el valor de y en la ecuación (ii)
4x 2 + 1225 + 9x 2 – 210x – 24x – 560 = 44
13x 2 – 186 + 621 = 0
13x 2 – 117x – 69x + 621 = 0
13x(x-9)-69(x-9) = 0
(x-9)(13x-69) = 0
Ya sea x – 9 = 0, entonces x = 9
o 13x – 69 = 0, luego x69/13 que no es posible
Entonces, x = 9
Por lo tanto, el vértice será (9,4)
Pregunta 21. Encuentra un punto que sea equidistante del punto A (-5, 4) y B (-1, 6). ¿Cuántos puntos de este tipo hay?
Solución:
Consideremos P (h, k) como el punto que equidista de los puntos A (-5, 4) y B (-1, 6).
Entonces, PA = PB
Por lo tanto, (PA) 2 = (PB) 2
Ahora por fórmula de distancia, obtenemos
(-5 – h) 2 + (4 – k) 2 = (-1 – h) 2 + (6 – k) 2
25 + h2 + 10h + 16 + k2 – 8k = 1h2 + 2h + 36 + k2 – 12k
25 + 10h + 16 – 8k = 1 + 2h + 36 – 12k
8h + 4k + 41 – 37 = 0
8h + 4k + 4 = 0
2h + k + 1 = 0 …….(i)
Punto medio de AB = ((-5 – 1)/2, (4 + 6)/2) = (-3, 5)
En el punto (-3, 5), de eq(i)
2h + k = 2(-3) + 6
-6 + 5 = -1
2h + k + 1 = 0
Entonces, el punto medio de AB satisface la Ec. (i).
Por lo tanto, un número infinito de puntos, de hecho, todos los puntos que son solución
de la ecuación 2h + k + 1 = 0, son equidistantes del punto A y B.
Reemplazando h, k, por x, y en la ecuación anterior, tenemos 2x + y + 1 = 0
Pregunta 22. El centro de un círculo es (2a, a – 7). Encuentra los valores de a si el círculo pasa por el punto (11, -9) y tiene un diámetro de 10√2 unidades.
Solución:

Según la pregunta
Distancia entre el centro C (2a, a – 1) y el punto P (11, -9), que se encuentran en el círculo = Radio del círculo
Entonces, Radio del círculo =
…..(i)
Dado que, longitud de diámetro = 10√2
Por lo tanto, longitud del radio = Longitud del diámetro/2
= 10√2/2 = 5√2
Ahora ponga este valor en la ecuación (i), obtenemos
Cuadrando en ambos lados, obtenemos
50 = (11 – 2a) 2 + (2 + a) 2
50 = 121 + 4a 2 – 44a + 4 + a 2 + 4a
5a 2 – 40a + 75 = 0
un 2 – 8a + 15 = 0
un 2 – 5a – 3a + 15 = 0
a(a-5)-3(a-5) = 0
(un – 5)(un – 3) = 0
Entonces, a = 3, 5
Por lo tanto, los valores requeridos de a son 5 y 3.
Pregunta 23. Ayush comienza a caminar de su casa a la oficina. En lugar de ir directamente a la oficina, va primero a un banco, de ahí a la escuela de su hija y luego llega a la oficina. ¿Cuál es la distancia extra recorrida por Ayush para llegar a la oficina? (Suponga que todas las distancias recorridas son en línea recta). Si la casa está situada en (2, 4), el banco en (5, 8), la escuela en (13, 14) y la oficina en (13, 26), y las coordenadas están en kilómetros.
Solución:

Según la figura
Distancia entre dos puntos
Ahora, distancia entre casa y banco.
Distancia entre el banco y el de la hija
Escuela
Distancia entre la escuela de la hija y la oficina
Distancia total (casa+banco+escuela+oficina) recorrida = 5 + 10 + 12 = 27 unidades
Distancia entre casa y oficinas
= 24,59 = 24,6 km
Entonces, la distancia extra recorrida por Ayush para llegar a su oficina = 27 – 24,6 = 2,4 km.
Por lo tanto, la distancia adicional requerida recorrida por Ayush es de 2,4 km.
Pregunta 24. Encuentra el valor de k, si el punto P (0, 2) es equidistante de (3, k) y (k, 5).
Solución:
Consideremos que P (0, 2) es equidistante de A (3, k) y B (k, 5)
PA = PB
=> PA 2 = PB 2
Por lo tanto, PA 2 = (0 – 3) 2 + (2 – k) 2
= (-3) 2 + (2 – k) 2
= k2 – 4k + 13
De manera similar, PB 2 = (k – 0) 2 + (5 – 2) 2
= k2 + (3) 2 = k2 + 9
Por lo tanto, PA = PB
PA 2 = PB 2
k2 – 4k + 13 = k2 + 9
-4k = 9 – 13
-4k = -4
k = -4/-4 = 1
Por lo tanto, K = 1.
Pregunta 25. Si (-4, 3) y (4, 3) son dos vértices de un triángulo equilátero, encuentra las coordenadas del tercer vértice, dado que el origen está en el
(yo) interiores,
(ii) el exterior del triángulo.
Solución:
Consideremos que el tercer vértice de un triángulo equilátero sea (x, y).
Entonces, los vértices son A (-4, 3), B (4,3) y C (x, y).
Sabemos que en un triángulo equilátero el ángulo entre dos
lado adyacente es 60 y los tres lados son iguales.
Por lo tanto, AB = BC = CA
AB2 = BC2 = CA2 … .. (i)
Ahora, tomando las dos primeras partes
AB 2 = BC 2
(4 + 4) 2 + (3 – 3) 2 = (x – 4) 2 + (y – 3) 2
64 + 0 = x 2 + 16 – 8x + y 2 + 9 – 6y
x 2 + y 2 – 8x – 6y = 39 …..(ii)
Ahora, tomando la primera y la tercera parte.
AB2 = CA2 _
(4 + 4) 2 + (3 – 3) 2 = (x – 4) 2 + (y – 3) 2
64 + 0 = x 2 + 16 – 8x + y 2 + 9 – 6y
x2 + y2 – 8x – 6y = 39
Al restar la ecuación (ii) de (iii), obtenemos
x = 0
Ahora, pon el valor de x en la ecuación (ii), obtenemos
0 + y 2 – 0 – 6y = 39
y 2 – 6y – 39 = 0
Por lo tanto, y =
Entonces, los puntos del tercer vértice son
(0, 3+√3)o(3 – 4√3)
Pero se da que, el origen está en el interior del ∆ABC y la coordenada x del tercer vértice es cero.
Entonces, la coordenada y del tercer vértice debe ser negativa.
Por lo tanto, la coordenada requerida del tercer vértice,
C = (0, 3 – 4√3)
Pregunta 26. Demuestre que los puntos (-3, 2), (-5, -5), (2, -3) y (4, 4) son los vértices de un rombo. Encuentra el área de este rombo.
Solución:
Consideremos que las coordenadas de los vértices A, B, C y D de un rombo son A (-3, 2), B (-5, -5), C (2, -3) y D (4, 4)
o AB 2 = (-2) 2 + (-7) 2 = 4 + 49 = 53
Del mismo modo, BC 2 = (2 + 5) 2 + (-3 + 5) 2
= (7) 2 + (2) 2 = 49 + 4 = 53
CD 2 = (4 – 2) 2 + (4 + 3) 2
= (2) 2 + (7) 2 = 4 + 48 = 53
y DA 2 = (-3 – 4) 2 + (2 – 4) 2
= (-7) 2 + (-2) 2 = 49 + 4 = 53
Por tanto, vemos que AB = BC = CD = DA = √53
Ahora diagonales AC =
y diagonal BD =
Por lo tanto, los lados son iguales pero las diagonales no son iguales
Por lo tanto, ABCD es un rombo.
Ahora encontramos el área del rombo = Producto de diagonal/2
= (5√2 × 9√2)/2
= 9/2
= 45 unidades cuadradas
Pregunta 27. Encuentra las coordenadas del circuncentro del triángulo cuyos vértices son (3, 0), (-1, -6) y (4, -1). Además, encuentre su circunradio.
Solución:

Consideremos que ABC es un triángulo cuyos vértices son A (3, 0), B (-1, -6) y C (4, -1)
Sea O el circuncentro del triángulo ABC y las coordenadas sean (x, y)
Por lo tanto, OA = OB = OC
OA 2 = OB 2 = OC 2
Ahora OA =
OA 2 = (x 2 – x 1 ) 2 + (y 2 – y 1 ) 2
= (x – 3) 2 + (y – 0) 2
= (x – 3) 2 + y 2
OB 2 = (x + 1) 2 + (y + 6) 2
y CO2 = (x – 4) 2 + (y + 1) 2
Por lo tanto, OA 2 = OB 2
(x – 3) 2 + y 2 = (x + 1) 2 + (y + 6) 2
x2 – 6x + 9 + y2 = x2 + 2x + 1 + y2 + 12y + 36
-6x – 2x – 12y = 1 + 36 – 9
-8x – 12y = 28
2x + 3y = -7 ……..(yo)
Por lo tanto, OB 2 = OC 2
(x + 1) 2 + (y + 6) 2 = (x – 4) 2 + (y + 1) 2
x2 + 2x + 1 + y2 + 12y + 36 = x2 – 8x + 16 + y2 + 2y + 1
2x + 12y + 37 + 8x – 2y = 17
10x + 10y = 17 – 37 = -20
x + y = -2 ……..(ii)
Al multiplicar la ecuación (i) por 1 y (ii) por 2, obtenemos
2x + 3y = -7
2x + 2y = -4
Ahora, al sustituir y = -3, obtenemos
x + y = -2
x-3 = -2
x = -2 + 3 = 1
Radio = OA =
= √13
Pregunta 28. Encuentra un punto en el eje x que sea equidistante de los puntos (7, 6) y (-3, 4).
Solución:
El punto requerido está en el eje x
Su ordenada será O
Entonces, las coordenadas del punto requerido P (x, 0)
Se da que el punto P equidista de los puntos A (7, 6) y B (-3, 4)
Ahora AP
Por lo tanto, AP 2 = (x – 7) 2 + 36
De manera similar, BP 2 = (x + 3) 2 + (0 – 4) 2
= (x + 3) 2 + 16
Por lo tanto, AP = BP
AP 2 = PA 2
Por lo tanto, (x – 7) 2 + 36 = (x + 3) 2 + 16
x2 – 14x + 49 + 36 = x2 + 6x + 9 + 16
x2 – 14x – x2 – 6x = 25 – 85
-20x = -60
X = -60/-20 = 3
Por lo tanto, el punto requerido será (3, 0)
Pregunta 29. (i) Demuestre que los puntos A (5, 6), B (1, 5), C (2, 1) y D (6, 2) son los vértices de un cuadrado.
(ii) Demuestre que los puntos A (2, 3), B (-2, 2), C (-1, -2) y D (3, -1) son los vértices de un cuadrado ABCD.
(iii) Nombre el tipo de triángulo PQR formado por el punto P(√2, √2), Q(- √2, – √2) y R (-√6, √6).
Solución:
(i) Los puntos dados son A (5, 6), B (1, 5), C (2, 1) y D (6, 2)
Ahora AB 2 = (x 2 – x 1 ) 2 + (y 2 – y 1 ) 2
= (1 – 5) 2 + (5 – 6) 2
= (-4) 2 + (-1) 2 = 16 + 1 = 17
Del mismo modo, BC = (2 – 1) 2 + (1 – 5) 2
= (1) 2 + (-4) 2
= 1 + 16 = 17
CD = (6 – 2) 2 + (2 – 1) 2 + (4) 2 + (1) 2
= 16 + 1 = 17
y DA = (5 – 6) 2 + (6 – 2) 2
= (-1) 2 + (4) 2
= 1 + 16 = 17
Diagonales CA 2 = (2 – 5) 2 + (1 – 6) 2
= (-3) 2 + (-5) 2
= 9 + 25
=34
y BD 2 = (6 – 1) 2 + (2 – 5) 2
= (5) 2 + (-3) 2
= 25 + 9 = 34
Concluimos que
AB = BC = CD = DA y diagonales AC = BD
Por lo tanto, ABCD es un cuadrado.
(ii) Dados los puntos A(2, 3), B(-2, 2), C(-1, -2) y D(3, -1)
Similarmente,
Por lo tanto, AB, BC, CD y DA son iguales y las diagonales AC y BD también son iguales
Por lo tanto, ABCD es un cuadrado.
(iii) Uso de la fórmula de la distancia
Como PQ = PR = RQ = 4, entonces, los puntos P, Q, R forman un triángulo equilátero.
Pregunta 30. Encuentra el punto en el eje x que es equidistante de los puntos (-2, 5) y (2, -3).
Solución:
Consideremos que el punto P se encuentra en el eje x
Entonces, las coordenadas del punto P ser (x, 0)
Se da que P es equidistante de A (-2, 5) y B (2, -3)
PA 2 = (x + 2) 2 + (-5) 2
= (x + 2) 2 + 25
PA 2 = (x – 2) 2 + (0 + 3) 2
= (x – 2) 2 + 9
AP = PA
Entonces, AP 2 = BP 2
(x + 2) 2 + 25 = (x – 2) 2 + 9
x2 + 4x + 4 + 25 = x2 – 2x + 4 + 9
x2 + 4x – x2 + 4x = 13 – 29
8x = -16
x = -16/8
x = -2
Por lo tanto, las coordenadas del punto P son (-2, 0)
Pregunta 31. Encuentra el valor de x tal que PQ = QR donde las coordenadas de P, Q y R son (6, -1), (1, 3) y (x, 8) respectivamente.
Solución:
Dado que las coordenadas de P (6, -1), Q(1, 3) y R(x, 8)
Además, PQ = QR
Usando la fórmula de la distancia
re =
Encontramos la longitud de PQ y QR
PQ 2 = (1 – 6) 2 + (3 + 1) 2
= (-5) 2 + (4) 2
= 25 + 16 = 41
QR2 = (x – 1) 2 + (8 – 3) 2
= (x – 1) 2 + (5) 2 = (x – 1) 2 + 25
Se da que PQ = QR
Entonces PQ 2 = QR 2
41 = (x – 1) 2 + 25
(x – 1) 2 = 41 – 25 = 16 = (±4) 2
x – 1 = ±4
Si x – 1 = 4, entonces x = 1 + 4 = 5
Si x – 1 = -4 entonces x = -4 + 1 = -3
Por lo tanto, el valor de x = 5, -3
Pregunta 32. Demuestra que los puntos (0, 0), (5, 5) y (-5, 5) son los vértices de un triángulo rectángulo isósceles.
Solución:
Consideremos que ABC es un triángulo cuyos vértices son A(0, 0), B(5, 5) y C(-5, 5)
Ahora
AB 2 = (√50) 2 = 50
De manera similar, BC 2 = (-5 – 5) 2 (5 – 5) 2
= (-10) 2 + (0) 2 = 100 + 0 = 100
y CA 2 = (0 + 5) 2 + (0 – 5) 2
= (5) 2 + (-5) 2 = 25 + 25 = 50
Aquí, concluimos que AB = CA
Además, AB 2 + CA 2 = 50 + 50 = 100 = BC 2
Por lo tanto, el triángulo ABC es un triángulo rectángulo.
Pregunta 33. Si los puntos P (x, y) equidistan de los puntos A (5, 1) y B (1,5), demuestre que x = y.
Solución:
Consideremos que P(x, y) es equidistante de los puntos A (5, 1) y B (1,5),
Se da que PA = PB
Además, PA 2 = PB 2
Ahora PA=
Al elevar al cuadrado ambos lados, obtenemos
(5 – x) 2 + (1 – y) 2 = (1 – x) 2 + (5 – y) 2
25 + x 2 – 10x + 1 + y 2 – 2y = 1 + x 2 – 2x + 25 + y 2 – 10y
-10x – 2y + 26 = -2x – 10y + 26
-10x – 2y = -2x – 10y
-10x + 2x = -10y + 2y
-8x = -8xy
x = y
Pregunta 34. Si Q (0, 1) es equidistante de P (5, -3) y R (x, 6) encuentra los valores de x. Halla también las distancias QR y PR.
Solución:
Dado que Q (0, 1) es equidistante de P (5, -3) y R (x, 6)
Entonces, PQ = RQ
Además, PA 2 = PB 2
Ahora
PQ 2 = 41
De manera similar, RQ 2 = (-x) 2 + (1 – 6) 2
= (-x) 2 + (-5) 2 = x 2 + 25
Se da que PQ = RQ
Entonces,x2 + 25 = 41
x2 = 41 – 25
x2 = (±4) 2
x = ±4
Ahora QR = √x 2 + 25 = √41
Entonces, cuando x = 4, entonces
o cuando x = -4, entonces
Pregunta 35. Encuentra los valores de y para los cuales la distancia entre los puntos P (2, -3) y Q (10, y) es de 10 unidades.
Solución:
Dado que la distancia entre P (2, -3) y Q (10, y) = 10
Asi que,
Al elevar al cuadrado ambos lados obtenemos
64 + (y + 3) 2 = 100
(y + 3) 2 = 100 – 64
(y + 3) 2 = 36
y + 3 = (±6) 2
Entonces, cuando y + 3 = 6, entonces y = 6 – 3 = 3
O cuando y + 3 = -6, entonces y = -6 – 3 = -9
Por lo tanto, y = 3, -9
Pregunta 36. Si el punto P (k – 1, 2) es equidistante de los puntos A (3, k) y B (k, 5), encuentra los valores de k.
Solución:
Dado que el punto P (k – 1, 2) es equidistante de A (3, k) y B (k, 5)
Entonces, PA = PB
Además, PA 2 = PB 2
(k – 1 – 3) 2 + (2 – k) 2 = (k – 1 – k) 2 + (2 – 5) 2
(k – 4) 2 + (2 – k) 2 = (-1) 2 + (-3) 2
k2 – 8k + 16 + 4 – 4k + k2 = 1 + 9
2k 2 – 12k + 20 – 10 = 0
2k 2 – 12k + 10 = 0
k 2 – k – 5k + 5 = 0
k(k-1)-5(k-5) = 0
(k – 1)(k – 5) = 0
O bien k – 1 = 0, entonces k = 1
o k – 5 = 0, entonces k = 5
Por lo tanto, k = 1, 5
Pregunta 37. Si el punto A (0, 2) es equidistante del punto B (3, p) y C (p, 5), encuentra p. Además, encuentre la longitud de AB.
Solución:
Dado que el punto A (0, 2) es equidistante de B (3, p) y C (p, 5)
Entonces, AB = AC
Además, AB 2 = AC 2
(0 – 3) 2 + (2 – p) 2 = (0 – p) 2 + (2 – 5) 2
9 + (2 – p) 2 = p 2 + 9
9 + 4 + pag 2 – 4 pag = pag 2 + 9
p 2 – 4 p + 13 – p 2 – 9 = 0
-4p – 4 = 0
-4p = -4
pag = -4/-4 = 1
p = 1
y AB =
Pregunta 38. Nombre el cuadrilátero formado, si lo hubiere, por los siguientes puntos, y justifique sus respuestas:
(i) A (-1, -2), B (1, 0), C (-1, 2), D (-3, 0)
(ii) A (-3, 5), B (3, 1), C (0, 3), D (-1, -4)
(iii) A (4, 5), B (7, 6), C (4, 3), D (1, 2)
Solución:

(i) Los puntos dados son A (-1, -2), B (1, 0), C (-1, 2), D (-3, 0)
Ahora
AB 2 = (x 2 – x 1 ) 2 + (y 2 – y 1 ) 2
= (1 + 1) 2 + (0 + 2) 2
= (2) 2 + (2) 2
= 4 + 4 = 8
De manera similar, BC 2 = (-1 – 1) 2 + (2 – 0) 2
= (-2) 2 + (2) 2
= 4 + 4 = 8
CD 2 = (-3 + 1) 2 + (0 – 2) 2
= (-2) 2 + (-2) 2
= 4 + 4 = 8
DA 2 = (-1 + 3) 2 + (-2 + 0) 2
= (2) 2 + (-2) 2
= 4 + 4 = 8
CA diagonal 2 = (-1 + 1) 2 + (2 + 2) 2
= (0) 2 + (4) 2 = 0 + 16 = 16
y BD 2 = (-3 – 1) 2 + (0 – 0) 2 = (-4) 2 + (0) = 16
Por lo tanto, los lados son iguales y las diagonales también son iguales.
Por lo tanto, el cuadrilátero ABCD es un cuadrado.
(ii) Los puntos dados son A (-3, 5), B (3, 1), C (0, 3), D (-1, -4)
Ahora AB
AB 2 = (x 2 – x 1 ) 2 + (y 2 – y 1 ) 2
= (3 + 3) 2 + (1 – 5) 2
= (6) 2 + (-4) 2
= 36 + 16 = 52
De manera similar, BC 2 = (0 – 3) 2 + (3 – 1) 2
= (-3) 2 + (2) 2
= 9 + 4 = 13
CD 2 = (-1 – 0) 2 + (-4 – 3) 2
= (-1) 2 + (-7) 2
= 1 + 49 = 50
AD 2 = (-3 + 1) 2 + (5 + 4) 2
= (-2) 2 + (9) 2
= 4 + 81 = 85
CA diagonal 2 = (0 + 3) 2 + (3 – 5) 2 = (3) 2 + (-2) 2 = 9 + 4 = 13
en el triangulo abc
La longitud de AB = √52, AC = √13, BC = √13
AC+ BC = √13 + √13 = 2√13
= √4 * 13 = √52
CA + BC = AB
Triángulo ABC no es posible
Por lo tanto, ABCD no es un cuadrilátero.
(iii) Puntos A (4, 5), B (7, 6), C (4, 3), D (1, 2)
Ahora AB
AB 2 = (x 2 – x 1 ) 2 + (y 2 – y 1 ) 2
= (7 – 4) 2 + (6 – 5) 2
= (3) 2 + (1) 2
= 9 + 1 = 10
De manera similar, BC 2 = (4 – 7) 2 + (3 – 6) 2
= (3) 2 + (-3) 2 = 9 + 9 = 18
CD 2 = (1 – 4) 2 + (2 – 3) 2
= (-3) 2 + (-1) 2
= 9 + 1 = 10
AD 2 = (4 – 1) 2 + (5 – 2) 2 = (3) 2 + (3) 2 = 9 + 9 = 18
Aquí AB = CD y BC = DA
CA diagonal 2 = (4 – 4) 2 + (3 – 5) 2
= (0) 2 + (-2) 2
= 0 + 4 = 4
y BD 2 = (1 – 7) 2 + (2 – 6) 2 = (-6) 2 + (-4) 2
= 36 + 16 = 52
Por lo tanto, los lados opuestos son iguales y las diagonales no son iguales.
Entonces, ABCD es un paralelogramo.
Pregunta 39. Halla la ecuación de la mediatriz del segmento de recta que une los puntos (7, 1) y (3, 5).
Solución:
Sean los puntos dados A (7, 1) y B (3, 5) y el punto medio sea M
Coordenadas del punto medio AB = ((7 + 3)/2, (1 + 5)/2) = (5, 3)
Ahora pendiente de AB(m 1 )
Pendiente de la perpendicular a AB(m 2 ) = -1/m 1 = -(-1) = -1
Entonces, la ecuación de la recta perpendicular que pasa por múltiplos y – y 1 = m(x – x 1 )
y-3 = 1(x-5)
y-3 = x-5
x – y = -3 + 5
x – y = 2
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA