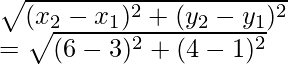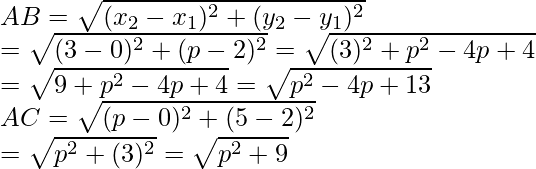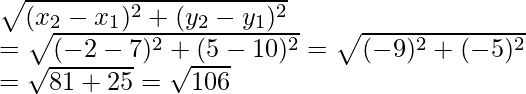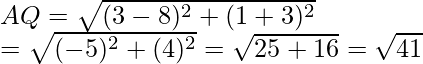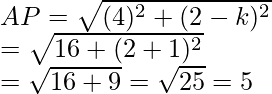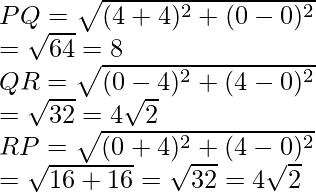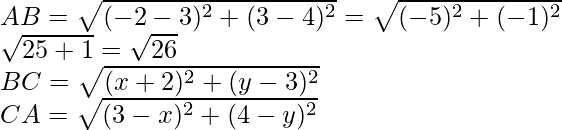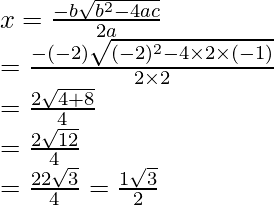Clase 10 Soluciones RD Sharma – Capítulo 14 Geometría de coordenadas – Ejercicio 14.2

Pregunta 40. Demuestra que los puntos (3, 0), (4, 5), (-1, 4) y (-2, -1) tomados en orden, forman un rombo. Además, encuentre su área.

Solución:

Consideremos que los puntos dados son A(3, 0), B(4, 5), C(-1, 4) y D(-2, -1)

Ahora encontramos la longitud de los lados y las diagonales,

Usando la fórmula de la distancia

Entonces AB = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(4-3)^2+(5-0)^2}$

AB ² = (4 + 3) ² + (5 – 0) ²

= (1) ² + (5) ²

= 1 + 25 = 26

Del mismo modo, BC ² = (-1 – 4) ² + (4 – 5) ²

= (-5) ² + (-1) ² = 25 + 1 = 26

CD ² = (-2 + 1) ² + (-1 – 4) ²

= (-1) ² + (-5) ² = 1 + 25 = 26

y AD ² = (3 + 2) ² + (0 + 1) ²

= (5) ² + (1) ² = 25 + 1 = 26

CA diagonal ² = (-1 – 3) ² + (4 – 0) ²

= (-4) ² + (4) ² = 16 + 16 = 32

y BD ² = (-2 – 4) ² + (-1 – 5) ²

= (-6) ² + (-6) ² = 36 + 36 = 72

Entonces, concluimos que los lados AB = BC = CD = DA y la diagonal AC no es igual a BD

Por lo tanto, ABCD es un rombo.

Ahora encontramos el área del rombo ABCD = Producto de diagonales/2

= (√32 × √72)/2

= (√16 × 2 × 2 × 36)/2

= 4 × 2 × 6/2

= 24 unidades cuadradas

Pregunta 41. En la disposición de los asientos de los escritorios en un salón de clases, tres estudiantes, Rohini, Sandhya y Bina, están sentados en A (3, 1), B (6, 4) y C (8, 6). ¿Crees que están sentados en una fila?

Solución:

Dado que A (3, 1), B (6, 4) y C (8, 6)

Ahora encontramos la longitud de los lados y las diagonales,

Usando la fórmula de la distancia

AB = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(6-3)^2+(4-1)^2}$

AB2 ⁼ (6 – 3) ² + (4 – 1) ²

= (3) ² + (3) ² = 9 + 9 = 18

Del mismo modo, BC ² = (8 – 6) ² + (6 – 4) ²

= (2) ² + (2) ² = 4 + 4 = 8

y BC ² = (8 – 6) ² + (6 – 4) ²

= (2) ² + (2) ² = 4 + 4 = 8

y CA ² = (3 – 8) ² + (1 – 6) ²

= (-5) ² + (-5) ² = 25 + 25 = 50

AB = √18 = √9 * 2 = 3√2

BC = √8 = √4 * 2 = 2√2

y CA = √50 = √25 * 2 = 5√2

AB + BC = 3√2 + 2√2 = 5√2 = CA

Por lo tanto, A, B y C son puntos colineales. Por lo tanto, están sentados en una línea.

Pregunta 42. Encuentra un punto en el eje y que sea equidistante de los puntos (5, -2) y (-3, 2).

Solución:

Supongamos que P es el punto que se encuentra en el eje y. Entonces, es x = 0, entonces las coordenadas de P son (0, y)

Se da que el punto P (0, y) equidista de los puntos A(5, -2) y B(-3, 2).

Entonces, PA = PB

Además, PA ² = PB ²

Ahora usando la fórmula de la distancia, obtenemos

(5 – 0) ² + (-2 – y) ² = (-3 – 0) ² + (2 – y) ²

25 + 4 + y ² + 4y = 9 + 4 – 4y + y ²

y2 ⁺ 4y + 4y – y2 ⁼ 13 – 29

8 años = -16

y = -16/8 = 2

Por lo tanto, el punto P requerido es (0,-2)

Pregunta 43. Encuentra una relación entre x e y tal que el punto (x, y) sea equidistante de los puntos (3, 6) y (-3, 4).

Solución:

Consideremos que P (x, y) es equidistante de A(3, 6) y B(-3, 4)

Entonces, PA = PB

Además, PA ² = PB ²

Ahora usando la fórmula de la distancia, obtenemos

$\sqrt{(x-3)^2+(y-6)^2}=\sqrt{[x-(-3)]^2+(y-4)^2}\\$

Al elevar al cuadrado ambos lados, obtenemos

(x – 3) ² + (y – 6) ² = (x + 3) ² + (y – 4) ²

x2 – 6x + 9 + ^y2^– 12y + 36 = x2 ⁺ 6x + 9 = ^y2 – 8y + 16

-6x – 12y + 45 = 6x – 8y + 25

-6x – 6x – 12y + 8y + 45 – 25 = 0

-12 – 4 años + 20 = 0

3x + y – 5 = 0

3x + y = 5

Pregunta 44. Si un punto A (0, 2) es equidistante de los puntos B (3, p) y C (p, 5), entonces encuentre el valor de p.

Solución:

Dado que el punto A (0, 2) es equidistante de los puntos B (3, p) y C (p, 5)

Ahora usando la fórmula de la distancia, obtenemos

$AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(3-0)^2+(p-2)^2}=\sqrt{(3)^2+p^2-4p+4}\\ =\sqrt{9+p^2-4p+4}=\sqrt{p^2-4p+13}\\ AC =\sqrt{(p-0)^2+(5-2)^2}\\ =\sqrt{p^2+(3)^2}=\sqrt{p^2+9}$

Se da que AB = AC

√p ² – 4p + 13 = √p ² + 9

Entonces, al elevar al cuadrado ambos lados, obtenemos

= pag ² – 4 pag + 13 = pag ² + 9

p ² – 4p – p ² = 9 – 13

-4p = -4

p = 1

Por lo tanto, el valor de p es 1

Pregunta 45. Demuestra que los puntos (7, 10), (-2, 5) y (3, -4) son los vértices de un triángulo rectángulo isósceles.

Solución:

Consideremos que los puntos son A (7, 10), B (-2, 5) y C (3, -4)

ahora hallamos la longitud de los lados

Usando la fórmula de la distancia

Ahora AB = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(-2-7)^2+(5-10)^2}=\sqrt{(-9)^2+(-5)^2}\\ =\sqrt{81+25}=\sqrt{106}$

Del mismo modo, BC = $\sqrt{(3+2)^2+(-4-5)^2}=\sqrt{106}$

y CA = $\sqrt{(3-7)^2+(-4-10)^2}=\sqrt{212}$

Entonces, concluimos que AB = BC = √106 y AB ² + BC ² = AC ²

Por lo tanto, ABC es un triángulo rectángulo isósceles

Pregunta 46. Si el punto P (x, 3) es equidistante de los puntos A (7, -1) y B (6, 8), encuentra el valor de xy la distancia AP.

Solución:

Se da que el Punto P (x, 3) es equidistante de los puntos A (7, -1) y B (6, 8)

Entonces, PA = PB

$\sqrt{(x-7)^2+(3+1)^2}=\sqrt{(x-6)^2+(3-8)^2}$

Al elevar al cuadrado ambos lados, obtenemos

(x – 7) ² + (4) ² = (x – 6) ² + (-5) ²

x2 – 14x ⁺ 49 + 16 = x2 – 12x ⁺ 36 + 25

x2 – 14x ⁺ 65 = x2 – 12x ⁺ 61

x2 – 14x + 12x – x2 ⁼⁶¹ – 65

-2x = -4

X = -4/-2 = 2

x = 2

ahora hallamos la distancia $AP=\sqrt{(2-7)^2+(4)^2}=\sqrt{(-5)^2+(4)^2} = \sqrt{41}$

Pregunta 47. Si A (3, y) es equidistante de los puntos P (8, -3) y Q (7, 6), encuentra el valor de y y encuentra la distancia AQ.

Solución:

Se da que el punto A (3, y) equidista de P (8, -3) y Q (7, 6)

Entonces, AP = AQ

$\sqrt{(3-8)^2+(y+3)^2} = \sqrt{(3-7)^2+(y-6)^2}$

Al elevar al cuadrado ambos lados, obtenemos

(3 – 8) ² + (y + 3) ² = (-4) ² + (y – 6) ²

(-5) ² + y ² + 6y + 9 = 16 + y ² – 12y + 36

25 + ^y2 + 6y + 9 = 16 + y2 – 12y ⁺ 36

y2 + 6y – y2 + 12y ⁼³⁶ – 9 – 25 + 16

18 años = 18

y = 18/18 = 1

y = 1

ahora hallamos la distancia $AQ=\sqrt{(3-8)^2+(1+3)^2}\\ =\sqrt{(-5)^2+(4)^2}=\sqrt{25+16}=\sqrt{41}$

Pregunta 48. Si (0, -3) y (0, 3) son los dos vértices de un triángulo equilátero, encuentra las coordenadas de su tercer vértice.

Solución:

Dado que A (0, -3) y B (0, 3) son los dos vértices de un triángulo equilátero ABC

Supongamos que las coordenadas del tercer vértice sean C (x, y)

En el triángulo equilátero, AC = AB

Asi que,

(x – 0) ² + (y + 3) ² = (0 – 0) ² + (3 + 3) ²

x ² + (y + 3) ² = 0 + (6) ² = 36

x2 + ^y2⁺ 6y + 9 = 36

x2 + ^y2⁺ 6y = 36 – 9 = 27 …….(i)

Además, BC = AB

(x-0) ² + (y-3) ² = 36

x2 + ^y2⁺ 9 – 6y = 36

x2 + ^{y2 – 6y}⁼ 36 – 9 = 27 ……..(ii)

Entonces, de la ecuación (i) y (ii), obtenemos

x2 + ^y2⁺ 6y = x2 + ^y2^– 6y

x2 + ^y2⁺ 6y – x2 – ^y2⁺ 6y = 0

12 años = 0

y = 0

Ahora pon el valor de y en la ecuación (i)

x2 + ^y2⁺ 6y = 27

x2 + ⁰ + 0 = 27

x = ±√27 = ±3√3

Entonces, las coordenadas del tercer punto son (3√3, 0) o (-3√3, 0)

Pregunta 49. Si el punto P (2, 2) es equidistante de los puntos A (-2, k) y B (-2k, -3), encuentra k. Además, encuentre la longitud de AP.

Solución:

Dado que el punto P (2, 2) es equidistante de los puntos A (-2, k) y B (-2k, -3)

Entonces, AP = BP

(2 + 2) ² + (2 – k) ² = (2 + 2k) ² + (2 + 3) ²

(4) ² + (2 – k) ² = (2 + 2k) ² + (5) ²

16 + 4 + k ² – 4k = 4 + 4k ² + 8k + 25

4k ² + 8k + 29 – 16 – 4 – k ² + 4k = 0

3k ² + 12k + 9 = 0

k2 ⁺ 4k + 3 = 0

k2 + k ⁺ 3k + 3 = 0

k(k + 1) + 3(k + 1) = 0

(k + 1)(k + 3) = 0

Entonces, el valor de k k + 1 = 0, entonces k = -1

o k + 3 = 0, entonces k = -3

Por lo tanto, k = -1, -3

ahora hallamos la distancia $AP=\sqrt{(4)^2+(2-k)^2}\\ =\sqrt{16+(2+1)^2}\\ =\sqrt{16+9}=\sqrt{25}=5$

Pregunta 50. Demuestre que ∆ABC, donde A (-2, 0), B (2, 0), C (0, 2) y ∆PQR, donde P (-4, 0), Q (4, 0), R (0, 4) son similares.

Solución:

Dado que en ∆ABC, los vértices son A (-2, 0), B (2, 0), C (0, 2)

En ∆PQR, los vértices son P (-4, 0), Q (4, 0), R (0, 4)

Demuestre que ∆ABC ~ ∆PQR

Asi que,

$AB=\sqrt{(2+2)^2+(0-0)^2}\\ =\sqrt{16}=4\\ BC=\sqrt{(0-2)^2+(2-0)^2}\\ =\sqrt{4+4}=\sqrt{8}=2\sqrt{2}$

Ahora, $PQ=\sqrt{(4+4)^2+(0-0)^2}\\ =\sqrt{64}=8\\ QR=\sqrt{(0-4)^2+(4-0)^2}\\ =\sqrt{32}=4\sqrt{2}\\ RP=\sqrt{(0+4)^2+(4-0)^2}\\ =\sqrt{16+16}=\sqrt{32}=4\sqrt{2}$

Entonces, AB/PQ = 4/8 = 1/2

BC/QR = 2√2/4√2 = 1/2

CA/PQ = 2√2/4√2 = 1/2

Entonces, AB/PQ = BC/QR = CA/RP

Mediante el uso de SSS

∆ABC ~ ∆PQR

Pregunta 51. Un triángulo equilátero tiene dos vértices en los puntos (3, 4) y (-2, 3). Encuentra las coordenadas del tercer vértice.

Solución:

Dado que A (3, 4) y B (-2, 3) son los dos vértices de un triángulo equilátero ABC

Supongamos que las coordenadas del tercer vértice sean C (x, y)

Ahora $AB=\sqrt{(-2-3)^2+(3-4)^2}=\sqrt{(-5)^2+(-1)^2}\\ \sqrt{25+1}=\sqrt{26}\\ BC=\sqrt{(x+2)^2+(y-3)^2}\\ CA=\sqrt{(3-x)^2+(4-y)^2}$

Como sabemos que en el triángulo equilátero, AB = BC = CA

Entonces, BC = AB

$\sqrt{(x+2)^2+(y-3)^2}=\sqrt{26}$

Al elevar al cuadrado ambos lados obtenemos

(x + 2) ² + (y – 3) ² = 26

x2 ⁺ 4x + 4 + ^y2 – 6y + 9 = 26

x ² + y ² + 4x – 6y + 13 = 26

x2 + ^y2⁺ 4x – 6y = 26 – 13 = 12 ………..(i)

Del mismo modo, CA = AB

$\sqrt{(3-x)^2+(4-y)^2}=\sqrt{26}$

Al elevar al cuadrado ambos lados obtenemos

(3 – x) ² + (4 – y) ² = 26

^{9 +} x2 – 6x + 16 + ^y2 – 8y = 26

x2 + ^{y2 – 6x – 8y}⁺ 25 = 26

x ² + y ² – 6x – 8y = 26 – 25 = 1 …….(ii)

Ahora, al restar la ecuación (ii) de (i), obtenemos

10x + 2y = 12

5x + y = 6 ……..(iii)

y = 6 – 5x

Ahora reemplazando el valor de y en la ecuación (i), obtenemos

x2 ⁺ (6 – 5x) ² + 4x – 6(6 – 5x) = 13

x ² + 36 + 25x ² – 60x + 4x – 36 + 30x – 13 = 0

26x ² – 26x – 13 = 0

2x ² – 2x – 1 = 0

Aquí, a = 2, b = -2, c = -1

$x=\frac{-b&pm;\sqrt{b^2-4ac}}{2a}\\ =\frac{-(-2)&pm;\sqrt{(-2)^2-4\times 2\times (-1)}}{2\times 2}\\ =\frac{2&pm;\sqrt{4+8}}{4}\\ =\frac{2&pm;\sqrt{12}}{4}\\=\frac{2&pm;2\sqrt{3}}{4}=\frac{1&pm;\sqrt{3}}{2}$

Cuando x = (1 + √3)/2, entonces y = 6 – 5x = 6 – 5((1 + √3)/2) = (7 – 5√3)/2

O cuando x = (1 – √3)/2, entonces y = 6 – 5x = 6 – 5((1 – √3)/2) = (7 + 5√3)/2

Por lo tanto, las coordenadas del punto C son ((1 + √3)/2, (7 – 5√3)/2) o ((1 – √3)/2, (7 + 5√3)/ 2)

Pregunta 52. Encuentra el circuncentro del triángulo cuyos vértices son (-2, -3), (-1, 0), (7, -6).

Solución:

Dado que los vértices de ∆ABC son A(-2, -3), B(-1, 0) y C(7, -6), y

supongamos que O es el circuncentro ∆ABC. Entonces, las coordenadas de O serán (x, y)

Entonces, OA = OB = OC

O OA ² = OB ² = OC ²

Ahora $OA = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

OA ² = (x + 2) ² + (y + 3) ²

= x2 ⁺ 4x + 4 + ^y2 + 6y + 9

= x2 + ^y2⁺ 4x + 6y + 13

OB ² = (x + 1) ² + (y + 0) ²

= x2 + ^2x + 1 + ^y2

= x2 + ^{y2 +}^2x + 1

CO2 ⁼ (x – 7) ² + (y + 6) ²

= x2 – 14x + 49 + ^y2⁺ 12y + 36

= x2 + ^{y2 – 14x}⁺ 12y + 85

AO ² = OB ²

x2 + ^y2⁺ 4x + 6y + 13 = x2 + y2 + ^2x⁺ 1

4x + 6y -2y = 1 – 13

2x + 6y = -12

x + 3y = -6 ………(yo)

OB ² = OC ²

x2 + ^{y2 +}^2x + 1 = x2 + ^{y2 – 14x}⁺ 12y + 85

2x + 14x – 2y = 85 – 1

16x – 12y = 84

4x – 3y = 21 ………(ii)

De la ecuación (i), obtenemos

x = -3y – 6

Al sustituir el valor de x en la ecuación (ii)

4(-3y – 6) – 3y = 21

-12 – 24 – 3 años = 21

-15 años = 21 + 24

-15 años = 45

y = -45/15 = -3

x = -3y – 6 = -3 × (-3) – 6

= + 9 – 6 = 3

Por lo tanto, las coordenadas de O son (3,-3)

Pregunta 53. Halla el ángulo subtendido en el origen por el segmento de recta cuyos extremos son (0, 100) y (10, 0).

Solución:

Consideremos que las coordenadas de los puntos finales de un segmento de línea son

A (0, 100), B (10, 0) y el origen es O (0, 0)

Entonces, el ángulo subtendido por la línea PQ en el origen es 90° o π/2

Pregunta 54. Encuentra el centro del círculo que pasa por (5, -8), (2, -9) y (2, 1).

Solución:

Dado que O es el centro del círculo y A(5, -8), B(2, -9) y C (2, 1) son los puntos del círculo.

Entonces, consideremos que las coordenadas de O sean (x, y)

Por lo tanto, OA = OB = OC

OA ² = OB ² = OC ²

Ahora $OA=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

OA ² = (x – 5) ² + (y + 8) ²

= x2 – 10x + 25 + ^y2⁺ 16y + 64

= x2 + ^{y2 – 10x}⁺ 16y + 89

De manera similar, OB ² = (x – 5) ² + (y + 9) ²

= x2 + ⁴ – 4x + ^y2 + 81 + 18y

= x2 + ^{y2 – 4x}⁺ 18y + 85

y OC ² = x ² – 4x + 4 + y ² – 2y + 1

= x2 + ^y2 – 4x – 2y + ⁵

AO ² = OB ²

x2 + ^{y2 – 10x}⁺ 16y + 89 = x2 + ^{y2 – 4x}⁺ 18y + 85

-10x + 4x + 16y – 18y = 85 – 89

-6x – 2y = -4

3x + y = 2 …….(yo)

OB ² = OC ²

x2 + ^{y2 – 4x}⁺ 18y + 85 = x2 + y2 – ^{4x –}^2y + 5

18 años + 2 años = 5 – 85

20 años = -80

y = -80/10 = -4

Ahora sustituimos el valor de y en la ecuación (i), obtenemos

3x + y = 2

3x – 4 = 2

3x = 2 + 4 = 6

X = 6/3 = 2

Por lo tanto, las coordenadas de O son (2,-4)

Pregunta 55. Si dos vértices opuestos de un cuadrado son (5, 4) y (1, -6), encuentra las coordenadas de los dos vértices restantes.

Solución:

Dado que los dos puntos opuestos de un cuadrado ABCD son A(5, 4) y C(1, -6)

Consideremos que las coordenadas de B sean (x, y).

Entonces, únete a AC

Como sabemos que los lados de un cuadrado son iguales, entonces,

AB = BC

AB ² = BC ²

(x – 5) ² + (y – 4) ² = (x – 1) ² + (y + 6) ²

x ² – 10x + 25 + y ² – 8y + 16 = x ² – 2x + 1 + y ² + 12y + 36

-10x + 2x – 8y – 12y = 37 – 41

-8x – 20y = -4

2x + 5y = 1

2x = 1 – 5y

x = (1 – 5 años)/2

entonces ABC es un triangulo rectangulo

Ahora, usando el teorema de Pitágoras, obtenemos

CA ² = AB ² + BC ²

(5 – 1) ² + (4 + 6) ² = x ² – 10x + 25 + y ² – 8y + 16 + x ² – 2x + 1 + y ² + 12y + 36

(4) ² + (10) ² = 2x ² + 2y ² – 12x + 4y + 78

16 + 100 = 2x ² + 2y ² – 12x + 4y + 78

2x ² + 2y ² – 12x + 4y + 78 – 16 – 100 = 0

2x ² + 2y ² – 12x + 4y – 38 = 0

x ² + y ² – 6x + 2y – 19 = 0 …..(i)

Ahora sustituyendo x = (1 – 5y)/2 en la ecuación (i), obtenemos

$(\frac{1-5y}{2})^2+y^2-6(\frac{1-5y}{2})+2y-19=0\\ \frac{1+25y^2-10y}{4}+y^2-3(1-5y)+2y-19=0$

1 + 25 años ² – 10 años + 4 años ² – 12 + 60 años + 8 años – 76 = 0

29 años ² + 58 años – 87 = 0

y ² + 2y – 3 = 0

y ² + 3y – y – 3 = 0

y(y+3) – 1(y+3) = 0

(y + 3)(y – 1) = 0

El valor de y puede ser y + 3 = 0, entonces y = -3

o y – 1 = 0, entonces y = 1

Cuando y = 1, entonces

x = (1 – 5 años)/2

= (1 – 5(1))/2

= -2

Cuando y = -3, entonces

x = (1 – 5(-3))/2

= 8

Entonces, los otros puntos del cuadrado ABCD son (-2,1) y (8,-3)

Pregunta 56. Encuentra el centro del círculo que pasa por (6, -6), (3, -7) y (3, 3).

Solución:

Consideremos O el centro de la circunferencia es (x, y)

Se da que el centro del círculo que pasa por (6, -6), (3, -7) y (3, 3)

Únase a OA, OB y OC

Entonces, OA = OB = OC

OA ² = (x -6 ) ² + (y + 6) ²

OB ² = (x – 3) ² + (y + 7) ²

y CO ² = (x – 3) ² + (y-3) ²

Como sabemos que OA ² = OB ²

Entonces, (x – 6) ² + (y + 6) ² = (x – 3) ² + (y + 7) ²

x2 – 12x + 36 + ^y2⁺ 12y + 36 = x2 ^– 6x + 9 + ^y2 + 14y + 49

x2 – 12x + 36 + ^y2⁺ 12y + 36 – x2 ⁺ 6x – 9 – ^y2 – 14y – 49 = 0

-12x + 12y + 72 + 6x – 14y – 58 = 0

-6x – 2y + 14 = 0

-6x – 2y = -14

3x + y = 7 …..(yo)

Además, OB ² = OC ²

(x – 3) ² + (y + 7) ² = (x – 3) ² + (y – 3) ²

x2 – 6x + 9 + ^y2⁺ 14y + 49 = x2 ^– 6x + 9 + ^y2 – 6y + 9

x2 + ^{y2 – 6x}⁺ 58 + 14y – x2 – ^y2⁺ 6x + 6y – 18 = 0

20 años + 40 = 0

20 años = -40

y = -40/20 = -2

3x + (-2) = 7

3x = 7 + 2 = 9

X = 9/3 = 3

Por lo tanto, las coordenadas del centro son (3,-2)

Pregunta 57. Dos vértices opuestos de un cuadrado son (-1, 2) y (3, 2). Encuentra las coordenadas de los otros dos vértices.

Solución:

Consideremos que ABCD es un cuadrado, en el que las coordenadas son A (-1, 2) y C (3, 2).

Supongamos que las coordenadas de B son (x, y)

Ahora, únete a AC

Como sabemos que los lados de un cuadrado son iguales, entonces,

AB = BC

AB ² = BC ²

Ahora $AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(x+1)^2+(y-2)^2}$

AB ² = (x + 1) ² + (y – 2) ²

De manera similar, BC ² = (x – 3) ² + (y – 2) ²

Como sabemos que AB = BC

Asi que,

(x + 1) ² + (y – 2) ² = (x – 3) ² + (y – 2) ²

(x + 1) ² = (x – 3) ²

x2 + ^2x + 1 = x2 ^– 6x + 9

x2 + ^2x + 6x – x2 = ⁹ – 1 = 8

8x = 8

X = 8/8 = 1

Ahora en el triángulo rectángulo ABC

CA ² = AB ² + BC ²

(3 + 1) ² + (2 – 2) ² = (x + 1) ² + (y – 2) ² + (x – 3) ² + (y – 2) ²

(4) ² + (0) ² = x ² + 2x + 1 + y ² – 4y + 4 + x ² – 6x + 9 + y ² – 4y + 4

16 = 2x ² + 2y ² – 4x – 8y + 18

2x ² + 2y ² – 4x – 8y = 16 – 18

2x ² + 2y ² – 4x – 8y = -2

x2 + ^{y2 –}^2x – 4y = -1 …….(i)

Ahora sustituimos el valor de x, en la ecuación (i), obtenemos

(1) ² + y ² – 2 × 1 – 4y = -1

1 + y ² – 2 – 4y = -1

y ² – 4y = -1 – 1 + 2 = 0

y(y – 4) = 0

Entonces el valor de y puede ser y = 0

o y – 4 = 0, entonces y = 4

Por lo tanto, las coordenadas de otros puntos serán (1, 0) y (1, 4)

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 10 Soluciones RD Sharma – Capítulo 14 Geometría de coordenadas – Ejercicio 14.2 | conjunto 3

Pregunta 40. Demuestra que los puntos (3, 0), (4, 5), (-1, 4) y (-2, -1) tomados en orden, forman un rombo. Además, encuentre su área.

Pregunta 41. En la disposición de los asientos de los escritorios en un salón de clases, tres estudiantes, Rohini, Sandhya y Bina, están sentados en A (3, 1), B (6, 4) y C (8, 6). ¿Crees que están sentados en una fila?

Pregunta 42. Encuentra un punto en el eje y que sea equidistante de los puntos (5, -2) y (-3, 2).

Pregunta 43. Encuentra una relación entre x e y tal que el punto (x, y) sea equidistante de los puntos (3, 6) y (-3, 4).

Pregunta 44. Si un punto A (0, 2) es equidistante de los puntos B (3, p) y C (p, 5), entonces encuentre el valor de p.

Pregunta 45. Demuestra que los puntos (7, 10), (-2, 5) y (3, -4) son los vértices de un triángulo rectángulo isósceles.

Pregunta 46. Si el punto P (x, 3) es equidistante de los puntos A (7, -1) y B (6, 8), encuentra el valor de xy la distancia AP.

Pregunta 47. Si A (3, y) es equidistante de los puntos P (8, -3) y Q (7, 6), encuentra el valor de y y encuentra la distancia AQ.

Pregunta 48. Si (0, -3) y (0, 3) son los dos vértices de un triángulo equilátero, encuentra las coordenadas de su tercer vértice.

Pregunta 49. Si el punto P (2, 2) es equidistante de los puntos A (-2, k) y B (-2k, -3), encuentra k. Además, encuentre la longitud de AP.

Pregunta 50. Demuestre que ∆ABC, donde A (-2, 0), B (2, 0), C (0, 2) y ∆PQR, donde P (-4, 0), Q (4, 0), R (0, 4) son similares.

Pregunta 51. Un triángulo equilátero tiene dos vértices en los puntos (3, 4) y (-2, 3). Encuentra las coordenadas del tercer vértice.

Pregunta 52. Encuentra el circuncentro del triángulo cuyos vértices son (-2, -3), (-1, 0), (7, -6).

Pregunta 53. Halla el ángulo subtendido en el origen por el segmento de recta cuyos extremos son (0, 100) y (10, 0).

Pregunta 54. Encuentra el centro del círculo que pasa por (5, -8), (2, -9) y (2, 1).

Pregunta 55. Si dos vértices opuestos de un cuadrado son (5, 4) y (1, -6), encuentra las coordenadas de los dos vértices restantes.

Pregunta 56. Encuentra el centro del círculo que pasa por (6, -6), (3, -7) y (3, 3).

Pregunta 57. Dos vértices opuestos de un cuadrado son (-1, 2) y (3, 2). Encuentra las coordenadas de los otros dos vértices.

Deja una respuesta Cancelar la respuesta