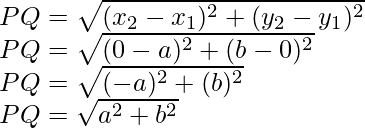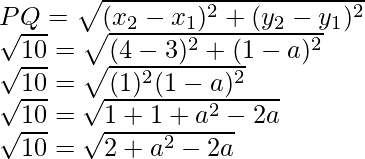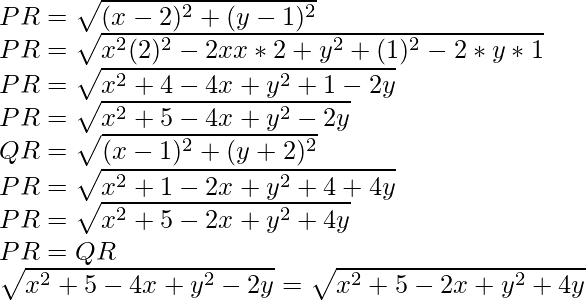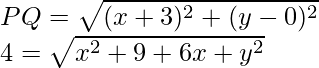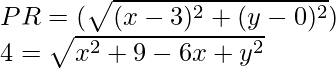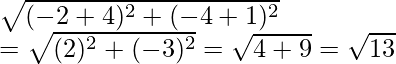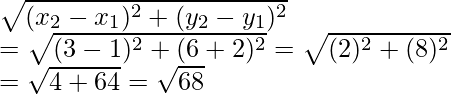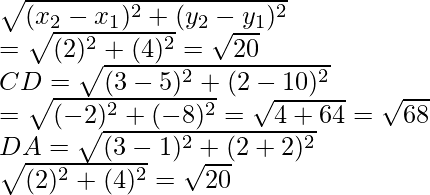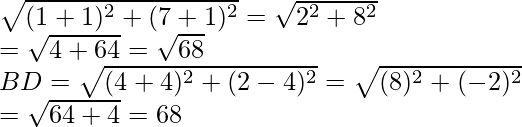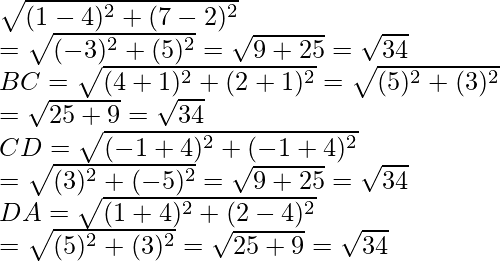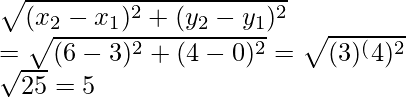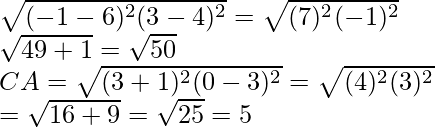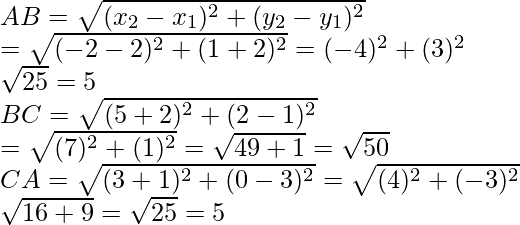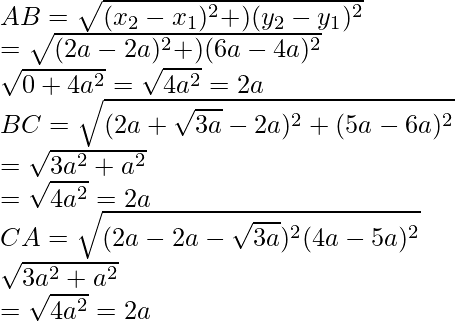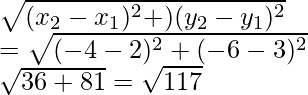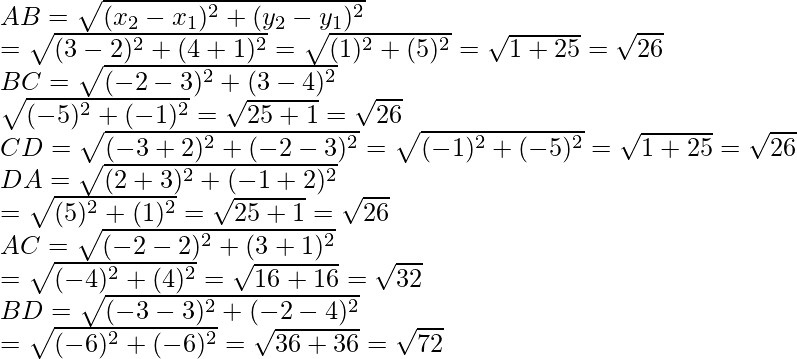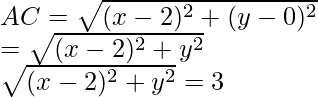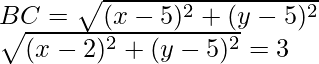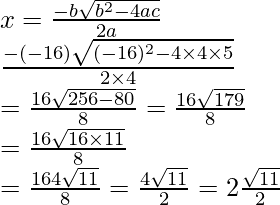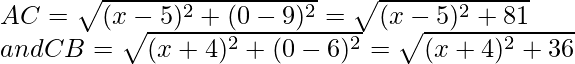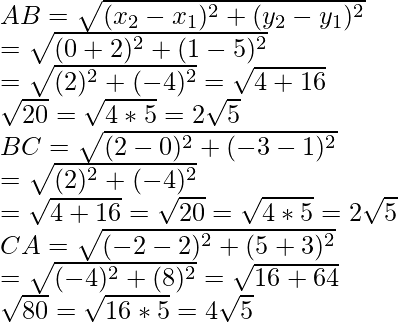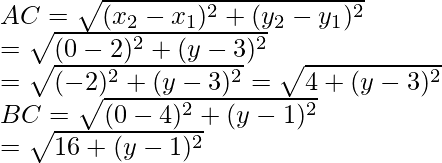Clase 10 Soluciones RD Sharma – Capítulo 14 Geometría de coordenadas – Ejercicio 14.2

Pregunta 1. Encuentra la distancia entre el siguiente par de puntos:

(yo) (-6, 7) y (-1,-5)

(ii) (a + b, b + c) y (a – b, c – b)

(iii) (a sen a, -b cos a) y (-a cos a, b sen a)

(iv) (a, 0) y (0, b)

Solución:

(i) Dado que P(-6, 7) y Q(-1, -5)

Entonces, x ₁ = -6, y ₁ = 7

x2 = -1, _y2₌ -5

Ahora encontramos la distancia entre PQ:

$PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ PQ=\sqrt{[-1-(-6)]^2+(-5-7)^2}\\ PQ=\sqrt{(-1+6)^2+(-5-7)^2}\\ PQ=\sqrt{(5)^2+(-12)^2}\\ PQ=\sqrt{25+144}\\ PQ=\sqrt{169}\\ PQ=13\\$

(ii) Dado que P(a + b, b + c) y Q(a – b, c – b)

Entonces, x ₁ = a + b, y ₁ = b + c

x ₂ = un – segundo, y ₂ = c – segundo

Ahora encontramos la distancia entre PQ:

$PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ PQ=\sqrt{[a-b-(a+b)]^2+(c-b-(b+c))^2}\\ PQ=\sqrt{(a-b-a-b)^2+(c-b-b-c)^2}\\ PQ=\sqrt{(-2b)^2+(-2b)^2}\\ PQ=\sqrt{4b^2+2b^2}\\ PQ=\sqrt{8b^2}\\ PQ=\sqrt{4*2b^2}\\ PQ=2\sqrt{2b}$

(iii) Dado que P(a sen a,-b cos a) y Q(-a cos a,b sen a)

Entonces, x ₁ = a sen a, y ₁ = -b cos a

x ₂ = a cos a, y ₂ = b sen a

Ahora encontramos la distancia entre PQ:

$PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ PQ=\sqrt{(-a\cos a-a\sin a)^2+[-b\sin a-(-b\cos a)]^2}\\ PQ=\sqrt{(-a\cos a)^2+(-a\sin a)^2+2(a-\cos a)(-a\sin a)+(b\sin a)^2+(-b\cos a)^2-2(b\sin a)(-b\cos a)}\\ PQ=\sqrt{a^2cos^2a+a^2\sin^2a+2a^2\cos a\sin a+b^2\sin^2a+b^2\cos^2a+2b^2\sin a\cos a}\\ PQ=\sqrt{a^2(\cos^2a+\sin^2a)+2a^2\cos a\sin a+b^2(\sin^2a+\cos^2a)+2b^2\sin a\cos a}\\ PQ=\sqrt{a^2*1+2a^2\cos a\sin a+b^2*12b^2\sin a\cos a}\\ PQ=\sqrt{a^2+b^2+2a^2\cos a\sin a+2b^2\sin a\cos a}\\ PQ=\sqrt{(a^2+b^2)+2\cos a\sin a(a^2+b^2)}\\ PQ=\sqrt{(a^2+b^2)+(1+2\cos a\sin a)}\\$

(iv) Dado que P(a, 0) y Q(0, b)

Entonces, x ₁ = a, y ₁ = 0

x2 = ₀ , y2 = _segundo

Ahora encontramos la distancia entre PQ:

$PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ PQ=\sqrt{(0-a)^2+(b-0)^2}\\ PQ=\sqrt{(-a)^2+(b)^2}\\ PQ=\sqrt{a^2+b^2}\\$

Pregunta 2. Encuentra el valor de a cuando la distancia entre los puntos (3, a) y (4, 1) es √10.

Solución:

Dado que el punto P(3, a) y Q(4, 1) y la distancia entre ellos es √10

Entonces, tenemos que encontrar el valor de a

Asi que,

$PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ \sqrt{10}=\sqrt{(4-3)^2+(1-a)^2}\\ \sqrt{10}=\sqrt{(1)^2(1-a)^2}\\ \sqrt{10}=\sqrt{1+1+a^2-2a}\\ \sqrt{10}=\sqrt{2+a^2-2a}$

Cuadrando en ambos lados obtenemos

(√10) ² = (√{2 + a ² – 2a}) ²

10 = 2 + un ² – 2a

un ² – 2a + 2 – 10 = 0

un ² – 2a – 8 = 0

Al dividir el término medio obtenemos

un ² – 4a + 2a – 8 = 0

a(a-4) + 2(a-4) = 0

(a – 4)(a + 2) = 0

a = 4, a = -2

Pregunta 3. Si los puntos (2, 1) y (1, 2) son equidistantes del punto (x, y) demuestra que x + 3y = 0.

Solución:

Dado que P(2, 1) y Q(1, -2) y R(x, y)

Además, PR = QR

$PR=\sqrt{(x-2)^2+(y-1)^2}\\ PR=\sqrt{x^2(2)^2-2xx*2+y^2+(1)^2-2*y*1}\\ PR=\sqrt{x^2+4-4x+y^2+1-2y}\\ PR=\sqrt{x^2+5-4x+y^2-2y}\\ QR=\sqrt{(x-1)^2+(y+2)^2}\\ PR=\sqrt{x^2+1-2x+y^2+4+4y}\\ PR=\sqrt{x^2+5-2x+y^2+4y}\\ PR=QR\\ \sqrt{x^2+5-4x+y^2-2y}=\sqrt{x^2+5-2x+y^2+4y}$

x2 ⁺ 5 – 4x + ^y2 – 2y = x2 ⁺ 5 – 2x + ^y2 + 4y

x2 ⁺ 5 – 4x + ^y2 – 2y = x2 ⁺ 5 – 2x + ^y2 + 4y

-4x + 2x – 2y – 4y = 0

-2x – 6y = 0

-2(x + 3y) = 0

x + 3y = 0/-2

x + 3y = 0

Por lo tanto probado

Pregunta 4. Encuentra los valores de x, y si la distancia del punto (x, y) desde (-3, 0) así como desde (3, 0) son 4.

Solución:

Dado que P(x, y), Q(-3, 0) y R(3, 0).

Además, PQ = PR = 4

Asi que,

$PQ=\sqrt{(x+3)^2+(y-0)^2}\\ 4=\sqrt{x^2+9+6x+y^2}$

Al elevar al cuadrado en ambos lados, obtenemos

(4) ² = (√x ² + 9 + 6x + y ² ) ²

16 = x2 ⁺ 9 + 6x + ^y2

x2 + y2 ⁼¹⁶ – 9 – 6x

x2 + y2 ⁼⁷ – 6x ……..(1)

$PR=(\sqrt{(x-3)^2+(y-0)^2})\\ 4=\sqrt{x^2+9-6x+y^2}$

Al elevar al cuadrado en ambos lados, obtenemos

(4) ² = (√x ² + 9 – 6x + y ² ) ²

16 = x2 ⁺ 9 – 6x + ^y2

x2 + y2 ⁼¹⁶ – 9 + 6x

x2 + y2 ⁼⁷ + 6x ……..(2)

De la ecuación (1) y (2)

7 – 6x = 7 + 6x

7 – 7 = 6x + 6x

0 = 12x

X = 12

Al sustituir el valor de x = 0 en la ecuación (2)

x2 + y2 ⁼⁷ + 6x

0 + y ² = 7 + 6 * 0

y ² = 7

y = ±√7

Pregunta 5. La longitud de un segmento de línea es de 10 unidades y las coordenadas de un punto final son (2, -3). Si la abscisa del otro extremo es 10, encuentre la coordenada del otro extremo.

Solución:

Sea la ordenada del otro extremo en y, entonces La distancia entre (2, -3) y (10, y) es

$=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(10-2)^2+(y+3)^2}$ = 10

Cuadrando en ambos lados obtenemos

(8) ² + (y + 3) ² = 100

64 + y ² + 6y + 9 = 100

y ² + 6y + 73 – 100 = 0

y ² + 6y – 27 = 0

y ² + 9y – 3y – 27 = 0

y(y + 9) – 3(y + 9) = 0

(y + 9)(y – 3) = 0

Cuando y + 9 = 0, entonces y = -9

o cuando y – 3 = 0, entonces y = 3

Entonces, las coordenadas serán -9 o 3

Pregunta 6. Demuestra que los puntos (-4, -1), (-2, -4), (4, 0) y (2, 3) son los vértices de un rectángulo.

Solución:

Consideremos que ABCD es un rectángulo cuyos vértices son

A(-4, -1), B(-2, -4), C(4, 0) y D(2, 3)

Ahora

AB = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

= $\sqrt{(-2+4)^2+(-4+1)^2}\\ =\sqrt{(2)^2+(-3)^2}=\sqrt{4+9}=\sqrt{13}$

Del mismo modo, CD =√13

DA = √52

y BC = √52

AC = √65 y BD = √65

Aquí, AB = CD y AD = BC

y diagonales AC = BD

Entonces, ABCD es un rectángulo.

Pregunta 7. Demuestra que los puntos A (1, -2), B (3, 6), C (5, 10) y D (3, 2) son los vértices de un paralelogramo.

Solución:

Los puntos dados son A (1, -2), B (3, 6), C (5, 10) y D (3, 2)

Ahora AB = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(3-1)^2+(6+2)^2}=\sqrt{(2)^2+(8)^2}\\ =\sqrt{4+64}=\sqrt{68}$

Del mismo modo BC = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(2)^2+(4)^2}=\sqrt{20}\\ CD=\sqrt{(3-5)^2+(2-10)^2}\\ =\sqrt{(-2)^2+(-8)^2}=\sqrt{4+64}=\sqrt{68} \\DA=\sqrt{(3-1)^2+(2+2)^2}\\ \sqrt{(2)^2+(4)^2}=\sqrt{20}$

Entonces, de lo anterior concluimos que AB = CD y AD = BC

Por lo tanto, ABCD es un paralelogramo.

Pregunta 8. Demuestra que los puntos A (1, 7), B (4, 2), C (-1, -1) y D (-4, 4) son los vértices de un cuadrado.

Solución:

Los puntos dados son A (1, 7), B (4, 2), C (-1,-1), D (-4, 4)

Si estos son los vértices de un cuadrado, entonces sus diagonales y sus lados son iguales.

CA = $\sqrt{(1+1)^2+(7+1)^2}=\sqrt{2^2+8^2}\\ =\sqrt{4+64}=\sqrt{68}\\ BD=\sqrt{(4+4)^2+(2-4)^2}=\sqrt{(8)^2+(-2)^2}\\ =\sqrt{64+4}=68$

Entonces, AC = BD

Ahora AB= $\sqrt{(1-4)^2+(7-2)^2}\\ =\sqrt{(-3)^2+(5)^2}=\sqrt{9+25}=\sqrt{34}\\ BC=\sqrt{(4+1)^2+(2+1)^2}=\sqrt{(5)^2+(3)^2}\\ =\sqrt{25+9}=\sqrt{34}\\ CD=\sqrt{(-1+4)^2+(-1+4)^2}\\ =\sqrt{(3)^2+(-5)^2}=\sqrt{9+25}=\sqrt{34}\\DA=\sqrt{(1+4)^2+(2-4)^2}\\ =\sqrt{(5)^2+(3)^2}=\sqrt{25+9}=\sqrt{34}$

Entonces, AB = BC = CD = DA y la diagonal AC = BD

Por lo tanto, la figura dada ABCD es un cuadrado.

Pregunta 9. Demuestra que los puntos (3, 0), (6, 4) y (-1, 3) son los vértices de un triángulo isósceles rectángulo.

Solución:

Los puntos dados son A(3, 0), B(6, 4) y C(-1, 3)

Ahora encontramos la longitud de AB = $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(6-3)^2+(4-0)^2}=\sqrt{(3)^(4)^2}\\ \sqrt{25}=5$

Del mismo modo, BC= $\sqrt{(-1-6)^2(3-4)^2}=\sqrt{(7)^2(-1)^2}\\ \sqrt{49+1}=\sqrt{50}\\ CA=\sqrt{(3+1)^2(0-3)^2}=\sqrt{(4)^2(3)^2}\\ =\sqrt{16+9}=\sqrt{25}=5$

De lo anterior concluimos que AB = CA y BC es el lado más largo

Ahora verificamos el teorema de Pitágoras,

Entonces, BC ² = AB ² + CA ²

BC ² = (5) ² + (5) ²

BC ² = 25 + 25

50= 50

Entonces, AB ² + CA ² = BC ²

Por lo tanto, el triángulo ABC dado es un triángulo rectángulo isósceles.

Pregunta 10. Demuestra que (2, -2), (-2, 1) y (5, 2) son los vértices de un triángulo rectángulo. Encuentra el área del triángulo y la longitud de la hipotenusa.

Solución:

Los puntos dados son A(2, -2), B(-2, 1) y C(5, 2)

Ahora encontramos la longitud de $AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(-2-2)^2+(1+2)^2}=(-4)^2+(3)^2\\ \sqrt{25}=5\\ BC=\sqrt{(5+2)^2+(2-1)^2}\\ =\sqrt{(7)^2+(1)^2}=\sqrt{49+1}=\sqrt{50}\\ CA=\sqrt{(3+1)^2+(0-3)^2}=\sqrt{(4)^2+(-3)^2}\\ \sqrt{16+9}=\sqrt{25}=5$

Vemos que AB = CA y BC es el lado más largo.

Ahora verificamos el teorema de Pitágoras,

Entonces, BC ² = AB ² + CA ²

BC ² = (5) ² + (5) ²

BC ² = 25 + 25

50= 50

Entonces, AB ² + CA ² = BC ²

Entonces, el triángulo ABC dado es un triángulo rectángulo

Ahora encontramos el área del triángulo ABC = 1/2 × Base × altura

= 1/2 × 5 × 5

= 25/2 unidades cuadradas

Y la longitud de la hipotenusa BC es √50.

Pregunta 11. Demuestra que los puntos (2a, 4a), (2a, 6a) y (2a + √3 a, 5a) son los vértices de un triángulo equilátero.

Solución:

Los puntos dados son A(2a, 4a), B(2a, 6a) y C(2a + √3 a, 5a)

Ahora encontramos la longitud de $AB=\sqrt{(x_2-x_1)^2+)(y_2-y_1)^2}\\ =\sqrt{(2a-2a)^2+)(6a-4a)^2}\\ \sqrt{0+4a^2}=\sqrt{4a^2}=2a\\ BC=\sqrt{(2a+\sqrt{3a}-2a)^2+(5a-6a)^2}\\ =\sqrt{3a^2+a^2}\\ =\sqrt{4a^2}=2a \\ CA=\sqrt{(2a-2a-\sqrt{3a})^2(4a-5a)^2}\\ \sqrt{3a^2+a^2}\\ =\sqrt{4a^2}=2a$

Entonces, concluimos que la longitud del lado AB = BC = CA = 2a

Por lo tanto, ∆ABC es un triángulo equilátero.

Pregunta 12. Demuestra que los puntos (2, 3), (-4, -6) y (1, 32) no forman un triángulo.

Los puntos dados son A(2, 3), B(-4, -6) y C(1, 32)

Ahora encontramos la longitud de AB = $\sqrt{(x_2-x_1)^2+)(y_2-y_1)^2}\\ =\sqrt{(-4-2)^2+(-6-3)^2}\\ \sqrt{36+81}=\sqrt{117}\\$

De manera similar, para BC = √89 y CA = √2

Como sabemos que la suma de dos lados de un triángulo siempre es mayor que el tercer lado

Entonces, BC+ CA= √89 + √2 no mayor que AB

Por lo tanto, los puntos dados no forman un triángulo.

Pregunta 13. Los puntos A (2, 9), B (a, 5) y C (5, 5) son los vértices de un triángulo ABC con ángulo recto en B. Encuentra los valores de a y, por lo tanto, el área de ∆ A B C.

Solución:

Dado que los puntos A (2, 9), B (a, 5) y C (5, 5) son los vértices de ∆ABC rectángulo en B.

Por el teorema de Pitágoras,

CA ² = AB ² + BC ² ………(i)

Ahora, por fórmula de distancia,

Encontramos la longitud de AB = $\sqrt{(a-2)^2+(5-9)^2}$

= $\sqrt{a^2+4-4a+16}=\sqrt{a^2-4a+20}\\ BC=\sqrt{(5-a)^2+(5-5)^2}\\ =\sqrt{(5-a)^2+0}=5-a\\ AC=\sqrt{(2-5)^2+(9-5)^2}\\ =\sqrt{(-3)^2+(4)^2}=\sqrt{9+16}=\sqrt{25}=5$ ]

Ahora ponga los valores de AB, BC y AC en la ecuación (i), obtenemos

$(5)^2=\sqrt{(a^2-4a+20)^2+(5-a)^2}$

25 = un ² – 4a + 20 + 25 + un ² – 10a

2a ² – 14a + 20 = 0

un ² – 7a + 10 = 0

un ² – 2a – 5a + 10 = 0

a(a-2)-5(a-2) = 0

(un – 5)(un – 5) = 0

a = 2, 5

Aquí, a ≠ 5, ya que en a = 5, la longitud de BC = 0. No es posible porque

los lados AB, BC y CA de un triángulo rectángulo.

Entonces, a = 2

Ahora, las coordenadas son A (2, 9), B (2, 5) y C (5, 5)

Ahora encontramos el área de ∆ABC = $\frac{1}{2}[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]$

= 1/2[2(5 – 5) + 2(5 – 9) + 5(9 – 5)]

= 1/2(0 – 8 + 20)

= 1/2 × 12

= 6

Por lo tanto, el área requerida de ∆ABC es 6sq. unidades.

Pregunta 14. Demuestra que el cuadrilátero cuyos vértices son (2, -1), (3, 4), (-2, 3) y (-3, -2) es un rombo.

Solución:

Los puntos dados son A(2, -1), B(3, 4), C(-2, 3) y D(-3, -2)

Ahora encontramos la longitud de los lados AB, CD, DA, BD y las diagonales AC, BD

$AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(3-2)^2+(4+1)^2}=\sqrt{(1)^2+(5)^2}=\sqrt{1+25}=\sqrt{26}\\ BC=\sqrt{(-2-3)^2+(3-4)^2}\\ \sqrt{(-5)^2+(-1)^2}=\sqrt{25+1}=\sqrt{26}\\ CD=\sqrt{(-3+2)^2+(-2-3)^2}=\sqrt{(-1)^2+(-5)^2}=\sqrt{1+25}=\sqrt{26}\\DA=\sqrt{(2+3)^2+(-1+2)^2}\\ =\sqrt{(5)^2+(1)^2}=\sqrt{25+1}=\sqrt{26}\\AC=\sqrt{(-2-2)^2+(3+1)^2}\\ =\sqrt{(-4)^2+(4)^2}=\sqrt{16+16}=\sqrt{32} \\BD=\sqrt{(-3-3)^2+(-2-4)^2}\\ =\sqrt{(-6)^2+(-6)^2}=\sqrt{36+36}=\sqrt{72}$

Ahora concluimos que AB = BC = CD = DA = √26 y la diagonal AC ≠ BD

Por lo tanto, ABCD es un rombo.

Pregunta 15. Dos vértices de un triángulo isósceles son (2, 0) y (2, 5). Encuentra el tercer vértice si la longitud de los lados iguales es 3.

Solución:

Consideremos que ABC es un triángulo isósceles cuyos dos vértices son A (2, 0) y B (2, 5)

Entonces, las coordenadas del tercer vértice C son (x, y)

Y también dado que AC = BC = 3

Ahora $AC=\sqrt{(x-2)^2+(y-0)^2}\\ =\sqrt{(x-2)^2+y^2}\\ \sqrt{(x-2)^2+y^2}=3$

Al elevar al cuadrado ambos lados, obtenemos

(x – 2) ² + y ² = 9

x2 – 4x + 4 + ^y2⁼ 9

x ² + y ² – 4x = 5 …….(yo)

Similarmente, $BC=\sqrt{(x-5)^2+(y-5)^2}\\ \sqrt{(x-2)^2+(y-5)^2}=3$

Al elevar al cuadrado ambos lados, obtenemos

(x-2) ² + (y-5) ² = 9

x2 – 4x + 4 + ^y2^– 10y + 25 = 9

x2 + ^y2 – 4x – 10y = -20 …….(ii ⁾

Ahora, al restar la ecuación (ii) de (i), obtenemos

10 años = 25

y = 25/10 = 5/2

Al sustituir el valor de y en la ecuación (i)

x ² – 4 x + (5/2) ² = 5

x ² – 4x + 25/4 – 5 = 0

4x ² – 16x + 25 – 20 = 0

4x ² – 16x + 5 + 5 = 0

Aquí a = 4, b = -16, c = 5

$x=\frac{-b&pm;\sqrt{b^2-4ac}}{2a}\\ \frac{-(-16)&pm;\sqrt{(-16)^2-4\times 4\times 5}}{2\times 4}\\ =\frac{16&pm;\sqrt{256-80}}{8}=\frac{16&pm;\sqrt{179}}{8}\\ =\frac{16&pm;\sqrt{16\times 11}}{8}\\ =\frac{16&pm;4\sqrt{11}}{8}=\frac{4&pm;\sqrt{11}}{2}=2&pm;\frac{\sqrt{11}}{2}$

Entonces, la coordenada de C será (2 + √11/2, 5/2) o (2 – √11/2, 5/2)

Pregunta 16. ¿Qué punto en el eje x es equidistante de (5, 9) y (-4, 6)?

Solución:

Sean las coordenadas de dos puntos A (5, 9), B (-4, 6)

El punto requerido está en el eje x

Sus coordenadas o coordenadas y serán 0

Sean las coordenadas del punto C (x, 0)

CA = CB

Ahora $AC=\sqrt{(x-5)^2+(0-9)^2}=\sqrt{(x-5)^2+81}\\ and\space CB=\sqrt{(x+4)^2+(0-6)^2}=\sqrt{(x+4)^2+36}$

$\sqrt{(x-5)^2+81}=\sqrt{(x+4)^2+36}$

Elevando al cuadrado ambos lados, obtenemos

(x – 5) ² + 81 = (x + 4) ² + 36

x2 – 10x ⁺ 25 + 81 = x2 ⁺ 8x + 16 + 36 – 10x – 8x

-18 = 52 – 106

-18x = -54

x = -54/18

x = 3

Por lo tanto, el punto requerido es (3, 0)

Pregunta 17. Demuestra que los puntos (-2, 5), (0, 1) y (2, -3) son colineales.

Solución:

Los puntos dados son A(-2, 5), B(0, 1) y C(2, -3)

Ahora encontramos la longitud de AB, BC y CA

$AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(0+2)^2+(1-5)^2}\\ =\sqrt{(2)^2+(-4)^2}=\sqrt{4+16}\\ \sqrt{20}=\sqrt{4*5}=2\sqrt{5}\\BC=\sqrt{(2-0)^2+(-3-1)^2}\\ =\sqrt{(2)^2+(-4)^2}\\ =\sqrt{4+16}=\sqrt{20}=\sqrt{4*5}=2\sqrt{5}\\ CA=\sqrt{(-2-2)^2+(5+3)^2}\\ =\sqrt{(-4)^2+(8)^2}=\sqrt{16+64}\\ \sqrt{80}=\sqrt{16*5}=4\sqrt{5}$

Ahora AB + BC = 2√5 + 2√5

Y CA = 4√5

AB + BC = CA

Por lo tanto, A, B y C son colineales

Pregunta 18. Las coordenadas del punto P son (-3, 2). Encuentre las coordenadas del punto Q que se encuentra en la línea que une P y el origen tal que OP = OQ.

Solución:

Dado que las coordenadas de P son (-3, 2) y el origen O es (0, 0)

Supongamos que las coordenadas de Q sean (x, y)

Aquí, O es el punto medio de la línea PQ

entonces usando la fórmula del punto medio obtenemos,

(x – 3)/2 = 0 y (y + 3)/2 = 0

x = 3, y = -2

Por lo tanto, las coordenadas del punto Q son (3, -2)

Pregunta 19. ¿Qué punto en el eje y es equidistante de (2, 3) y (-4, 1)?

Solución:

El punto requerido se encuentra en el eje y

su abscisa será cero

Entonces, supongamos que el punto sea C (0, y) y A (2, 3), B (-4, 1)

Ahora, encontramos la longitud de AC y BC

$AC=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ =\sqrt{(0-2)^2+(y-3)^2}\\ =\sqrt{(-2)^2+(y-3)^2}=\sqrt{4+(y-3)^2}\\BC=\sqrt{(0-4)^2+(y-1)^2}\\ =\sqrt{16+(y-1)^2}\\$

Aquí, concluimos que AC = BC

Asi que, $\sqrt{4+(y-3)^2}=\sqrt{16+(y-1)^2}$

Al elevar al cuadrado ambos lados, obtenemos

4 + (y – 3) ² = 16 + (y – 1) ²

4 + ^y2 + 9 – 6y = 16 + y2 ⁺ 1 – 2y

-6 años + 2 años = 17 – 13

-4y = 4 = y = 4/-4 = 1

Por lo tanto, las coordenadas del punto requerido son (0,-1)

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 10 Soluciones RD Sharma – Capítulo 14 Geometría de coordenadas – Ejercicio 14.2 | Serie 1

Pregunta 1. Encuentra la distancia entre el siguiente par de puntos:

Pregunta 2. Encuentra el valor de a cuando la distancia entre los puntos (3, a) y (4, 1) es √10.

Pregunta 3. Si los puntos (2, 1) y (1, 2) son equidistantes del punto (x, y) demuestra que x + 3y = 0.

Pregunta 4. Encuentra los valores de x, y si la distancia del punto (x, y) desde (-3, 0) así como desde (3, 0) son 4.

Pregunta 5. La longitud de un segmento de línea es de 10 unidades y las coordenadas de un punto final son (2, -3). Si la abscisa del otro extremo es 10, encuentre la coordenada del otro extremo.

Pregunta 6. Demuestra que los puntos (-4, -1), (-2, -4), (4, 0) y (2, 3) son los vértices de un rectángulo.

Pregunta 7. Demuestra que los puntos A (1, -2), B (3, 6), C (5, 10) y D (3, 2) son los vértices de un paralelogramo.

Pregunta 8. Demuestra que los puntos A (1, 7), B (4, 2), C (-1, -1) y D (-4, 4) son los vértices de un cuadrado.

Pregunta 9. Demuestra que los puntos (3, 0), (6, 4) y (-1, 3) son los vértices de un triángulo isósceles rectángulo.

Pregunta 10. Demuestra que (2, -2), (-2, 1) y (5, 2) son los vértices de un triángulo rectángulo. Encuentra el área del triángulo y la longitud de la hipotenusa.

Pregunta 11. Demuestra que los puntos (2a, 4a), (2a, 6a) y (2a + √3 a, 5a) son los vértices de un triángulo equilátero.

Pregunta 12. Demuestra que los puntos (2, 3), (-4, -6) y (1, 32) no forman un triángulo.

Pregunta 13. Los puntos A (2, 9), B (a, 5) y C (5, 5) son los vértices de un triángulo ABC con ángulo recto en B. Encuentra los valores de a y, por lo tanto, el área de ∆ A B C.

Pregunta 14. Demuestra que el cuadrilátero cuyos vértices son (2, -1), (3, 4), (-2, 3) y (-3, -2) es un rombo.

Pregunta 15. Dos vértices de un triángulo isósceles son (2, 0) y (2, 5). Encuentra el tercer vértice si la longitud de los lados iguales es 3.

Pregunta 16. ¿Qué punto en el eje x es equidistante de (5, 9) y (-4, 6)?

Pregunta 17. Demuestra que los puntos (-2, 5), (0, 1) y (2, -3) son colineales.

Pregunta 18. Las coordenadas del punto P son (-3, 2). Encuentre las coordenadas del punto Q que se encuentra en la línea que une P y el origen tal que OP = OQ.

Pregunta 19. ¿Qué punto en el eje y es equidistante de (2, 3) y (-4, 1)?

Deja una respuesta Cancelar la respuesta