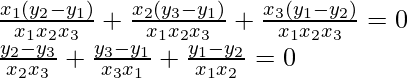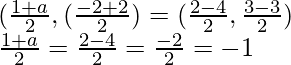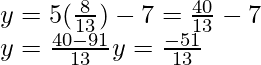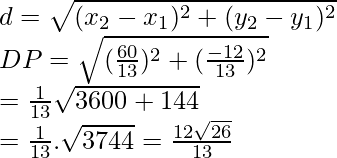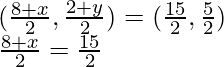Clase 10 Soluciones RD Sharma – Capítulo 14 Geometría de coordenadas – Ejercicio 14.5

Pregunta 23. Demuestra que los puntos (a, 0), (0, b) y (1, 1) son colineales si, 1/a + 1/b = 1.

Solución:

Supongamos que los puntos son A (a, 0), B (0, b) y C (1, 1) forman un triángulo ABC

Área de ∆ABC = 1/2[x ₁ (y ₂ – y ₃ ) + (y ₃ – y ₁ )x ₂ + x ₃ (y ₁ – y ₂ )]

= 1/2[a(b – 1) + 0(1 – 0) + 1(0 – b)]

= 1/2[ab – a + 0 + 1(-b)]

= 1/2[ab – a – b]

Si los puntos son colineales, entonces el área de ∆ABC = 0

⇒1/2(ab – a – b) = 0

⇒ ab – a – b = 0

⇒ ab = a + b

Ahora al dividir por ab, obtenemos

$\frac{ab}{ab}=\frac{a}{ab}+\frac{b}{ab}$

⇒ $1=\frac{1}{b}+\frac{1}{a}⇒\frac{1}{a}+\frac{1}{b}=1$

Pregunta 24. El punto A divide el conjunto de P (-5, 1) y Q (3, 5) en la razón k : 1. Encuentra los dos valores de k para los cuales el área de ∆ABC donde B es (1, 5 ) y C (7, -2) es igual a 2 unidades.

Solución:

Supongamos que las coordenadas de A sean (x, y) que divide la unión de P (-5, 1) y Q (3, 5) en la razón.

Entonces, las coordenadas de A serán $(\frac{mx_2+nx_1}{m+n},\frac{my_2+ny_1}{m+n})$

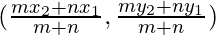
o $(\frac{k*3+1*(-5)}{k+1},\frac{k(5)+1(1)}{k+1})$ o $(\frac{3k-5}{k+1},\frac{5k+1}{k+1})$

Se da que el área de ∆ABC es 2 unidades y los vértices son B(1, 5), C(7, -2) y A son los vértices

Entonces, Área de ∆ABC = 1/2[x ₁ (y ₂ – y ₃ ) + (y ₃ – y ₁ )x ₂ + x ₃ (y ₁ – y ₂ )]

⇒ $2=\frac{1}{2}[\frac{3k-5}{k+1}(5+2)+1(-2-\frac{5k+1}{k+1}+7(\frac{5k+1}{k+1}-5)]$

⇒ $2=\frac{1}{2}[\frac{3k-5}{k+1}*7-2-\frac{5k+1}{k+1}+7(\frac{5k+1}{(k+1)-35})]\\ ⇒4=[\frac{21k-35}{k+1}-\frac{5k+1}{k+1}+\frac{35k+7}{k+1}-37]\\ ⇒4=[\frac{21k-35-5k+1+35k+7-37k-37}{k+1}]\\ ⇒|\frac{14k-66}{k+1}|=&pm;4$

(i) (14k – 66)(k + 1) = 4 ⇒ 14k – 66 = 4k + 4

⇒ 14k – 4k = 66 + 4

⇒10k = 70

⇒ k = 70/10 = 7

(ii) (14k – 66)(k + 1) = -4 ⇒ 14 – 66 = -4k – 4

⇒ 14k + 4k = -4 + 66 ⇒ 18k = 62

⇒ k = 62/18 = 31/9

Por lo tanto, el valor de k es 7, 31/9

Pregunta 25. El área de un triángulo es 5. Dos de sus vértices son (2, 1) y (3, -2). El tercer vértice se encuentra en y = x + 3. Encuentra el tercer vértice.

Solución:

Consideremos que ABC es un triángulo cuyos vértices son (2, 1), (3, -2) y (x, y)

También el área del triángulo ABC es 5

Asi que,

Área de ∆ABC = 1/2[x ₁ (y ₂ – y ₃ ) + (y ₃ – y ₁ )x ₂ + x ₃ (y ₁ – y ₂ )]

5 = 1/2[x(1 + 2) + 2(-2 – y) + 3(y – 1)]

10 = [3x-4-2y+3y-3]

10 = 3x + y – 7

3x + y = 10 + 7

3x + y = 17

Pero se da que el punto (x, y) está en y = x + 3

Entonces, 3x + x + 3 = 17

⇒ 4x = 17 – 3

4x = 14

⇒ x = 7/2

y y = x + 3 = 7/2 +3 = 13/2

Por lo tanto, el tercer vértice es (7/2, 13/2)

Pregunta 26. Se dan cuatro puntos A (6, 3), B (-3, 5), C (4, -2) y D (x, 3x) de tal forma que 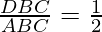$\frac{△DBC}{△ABC}=\frac{1}{2}$ , ¿encontrar x?

Solución:

Supongamos que ABCD es un cuadrilátero cuyos vértices son A (6, 3), B (-3, 5), C (4, -2) y D (x, 3x)

Ahora, AC y BD están unidos

Área del triángulo = 1/2[x ₁ (y ₂ – y ₃ ) + (y ₃ – y ₁ )x ₂ + x ₃ (y ₁ – y ₂ )]

= 1/2 [6(5 + 2) + (-3)(-2 – 3) + 4(3 – 5)]

= 1/2 [6 * 7 + (-3)(-5) + 4(-2)]

= 1/2 [42 + 15 – 8] = 49/2

y área de △DBC,

= 1/2[x(5 + 2) + (-3)(-2 – 3x) + 4(3x – 5)]

= 1/2[7x + 6 + 9x + 12x – 20]

= 1/2[28x – 14] = 14x – 7

Ahora, $\frac{∆DBC}{∆ABC}$ [Tex]=\frac{14x-7}{\frac{49}{2}} [/Tex]

$=\frac{(14x-7)*2}{49}$

$|\frac{2(14x-7)}{49}|=\frac{1}{2}⇒4|14x-7|=&pm;49$

Si 56x – 28 = 49

⇒ 56x = 49 + 28 = 77

⇒ x = 77/56 = 11/8

Si 4(14x – 7) = 49

⇒56x – 28 = -49

⇒56x = -49 + 28 = -21

⇒x = -21/56 = -3/8

x = 11/8 o -3/8

Pregunta 27. Si tres puntos (x ₁ , y ₁ ), (x ₂ , y ₂ ), (x ₃ , y ₃ ) están en la misma recta, prueba que

$\frac{y_2-y_3}{x_2x_3}+\frac{y_3-y_1}{x_3x_1}+\frac{y_1-y_2}{x_1x_2}=0$

Solución:

Supongamos que ABC es un triángulo cuyos vértices son (x ₁ , y ₁ ), (x ₂ , y ₂ ), (x ₃ , y ₃ )

Área de ∆ABC = 1/2[x ₁ (y ₂ – y ₃ ) + (y ₃ – y ₁ )x ₂ + x ₃ (y ₁ – y ₂ )]

Los puntos están en la misma línea, entonces

[x ₁ (y ₂ – y ₃ ) + (y ₃ – y ₁ )x ₂ + x ₃ (y ₁ – y ₂ )] = 0

Al dividir por x ₁ x ₂ x ₃ , obtenemos

$\frac{x_1(y_2-y_1)}{x_1x_2x_3}+\frac{x_2(y_3-y_1)}{x_1x_2x_3}+\frac{x_3(y_1-y_2)}{x_1x_2x_3}=0\\ \frac{y_2-y_3}{x_2x_3}+\frac{y_3-y_1}{x_3x_1}+\frac{y_1-y_2}{x_1x_2}=0$

Pregunta 28. Halla el área de un paralelogramo ABCD si tres de sus vértices son A (2, 4), B (2 + √3, 5) y C (2, 6).

Solución:

Dado que ABCD es un ||gm cuyos vértices son A (2, 4), B (2 + √3, 5) y C (2, 6).

Ahora dibuja una diagonal AC de ||gm ABCD

La diagonal divide el ||gm en dos triángulos de igual área

Área de ∆ABC = 1/2[x ₁ (y ₂ – y ₃ ) + (y ₃ – y ₁ )x ₂ + x ₃ (y ₁ – y ₂ )]

= 1/2 [2(5 – 6) + (2 + √3)(6 – 4) + 2(4 – 5)]

= 1/2 [2 * (-1) + (2 + √3) * 2 + 2 * (-1)]

= 1/2 [-2 + 4 + 2√3 – 2] = 1/2 (2√3) = √3 unidades cuadradas

Entonces, el área de ||gm ABCD = 2 * área(△ABC)

= 2 * (√3) = 2√3 unidades cuadradas

Pregunta 29. Encuentra el valor (s) de k para el cual los puntos (3k – 1, k – 2), (k, k – 7) y (k – 1, -k – 2) son colineales.

Solución:

Supongamos que el ABC es un triángulo cuyos vértices son A(3k – 1, k – 2), B(k, k – 7) y C(k – 1, -k – 2)

y A, B, C son colineales

Área de ∆ABC = 1/2[x ₁ (y ₂ – y ₃ ) + (y ₃ – y ₁ )x ₂ + x ₃ (y ₁ – y ₂ )]

= 1/2[(3k – 1)(k – 7 + k + 2) + k(-k – 2 – k + 2) + (k – 1)(k – 2 – k + 7)]

= 1/2 [(3k – 1)(2k – 5) + k(-2k + (k – 1) * 5)]

= 1/2 [6k ² – 15k – 2k + 5 – 2k ² + 5k – 5]

= 1/2[4k ² – 12k] = 2k ² – 6k

= 2k(k – 3)

Como sabemos que los puntos son colineales

entonces, Área de ABC=0

2k(k – 3) = 0

2k = 0 o k – 3 = 0, luego k = 0 o k = 3

Por lo tanto, k = 0, 3

Pregunta 30. Si los puntos A (-1, -4), B (b, c) y C (5, -1) son colineales y 2b + c = 4, encuentra los valores de b y c.

Solución:

Supongamos que el ABC es un triángulo cuyos vértices son A (-1, -4), B (b, c) y C (5, -1)

y A, B, C son colineales

Área de ∆ABC = 1/2[x ₁ (y ₂ – y ₃ ) + (y ₃ – y ₁ )x ₂ + x ₃ (y ₁ – y ₂ )]

= 1/2 [-1(c + 1) + b(-1 + 4) + 5(-4 – c)]

= 1/2 [-c – 1 – b + 4b – 20 – 5c]

= 1/2 [3b – 6c – 21]

Como sabemos que los puntos son colineales

entonces, Area del triangulo ABC = 0

1/2(2b – 6c – 21) = 0

⇒3b – 6c = 21

3b – 6c = 21 ———–(yo)

y 2b + c = 4 ———-(ii)

⇒c = 4 – 2b

Al sustituir el valor de c en la ecuación (i), obtenemos

⇒3b – 6(4 – 2b) = 21

⇒3b – 24 + 12b = 21

15b = 21 + 24 = 45

⇒b = 45/15 = 3

c = 4 – 2b = 4 – 2 * 3 = 4 – 6 = -2

b = 3, c = -2

Pregunta 31. Si los puntos A (-2, 1), B (a, b) y C (4, -1) son colineales y a – b = 1, encuentre los valores de a y 6.

Solución:

Supongamos que el ABC es un triángulo cuyos vértices son A (-2, 1), B (a, b) y C (4, -1)

y A, B, C son colineales

Área de ∆ABC = 1/2[x ₁ (y ₂ – y ₃ ) + (y ₃ – y ₁ )x ₂ + x ₃ (y ₁ – y ₂ )]

= 1/2 [-2(b + 1) + a(-1 – 1) + 4(1 – b)]

= 1/2[-2b – 2 – 2a + 4 – 4b]

= 1/2 [-2b – 2 – 2a + 4 – 4b]

= 1/2 [-2a – 6b + 2] = -a – 3b + 1

Como sabemos que los puntos son colineales

entonces, Area del triangulo ABC = 0

-a – 3b + 1 = 0

a + 3b = 1 ————(yo)

a = 1 – 3b

y dado que a – b = 1 ————(ii)

Al resolver las ecuaciones (i) y (ii), obtenemos

4b = 0 ⇒ b = 0

Por lo tanto, a = 1 – 3b = 1 – 3 * 0 = 1 – 0 = 1

a = 1, b = 0

Pregunta 32. Si los puntos A (1, -2), B (2, 3), C (a, 2) y D (-4, -3) forman un paralelogramo, encuentra el valor de a y la altura del paralelogramo tomando como base a AB.

Solución:

Dado que ABCD es un paralelogramo cuyos vértices son A (1, -2), B (2, 3), C (a, 2) y D (-4, -3)

Como sabemos, las diagonales se bisecan

es decir, punto medio de AC = punto medio de BD

⇒ $(\frac{1+a}{2},(\frac{-2+2}{2})=(\frac{2-4}{2},\frac{3-3}{2})\\ ⇒\frac{1+a}{2}=\frac{2-4}{2}=\frac{-2}{2}=-1$

= 1/2[x ₁ (y ₂ – y ₃ ) + (y ₃ – y ₁ )x ₂ + x ₃ (y ₁ – y ₂ )]

⇒1 + a = -2

⇒a = -3

Entonces, el valor requerido de a es -3

Dado que, AB como base de un ||gm y trazó una perpendicular de A a AB

que se encuentran con AB en P. Entonces, DP es una altura de un ||gm.

Ahora, la ecuación de base AB, pasando por los puntos (1, -2) y (2, 3) es

⇒ $(y-y_1)=\frac{y_2-y_1}{x_2-x_1}(x-x_1)$

⇒(y + 2)= $\frac{3+2}{2-1}(x-1)$

⇒(y + 2) = 5(x – 1)

⇒5x – y = 7 ————(yo)

Entonces, la pendiente de AB, digamos $m_1=\frac{y_2-y_1}{x_2-x_1}=\frac{3+2}{2-1}=5$

Sea la pendiente de DP m ₂ .

Ya que, DP es perpendicular a AB.

Por condición de perpendicularidad

metro ₁ * metro ₂ = -1 ⇒ 5 * metro ₂ = -1

⇒m2 ₌ -1/5

Ahora, ec. de DP, con pendiente (-1/5)

y pasando el punto (-4,-3) es (y – y ₁ ) = m ₂ (x – x ₁ )

⇒ $(y+3)=-\frac{1}{5}(x+4)$

⇒5y + 15 = -x – 4

⇒x + 5y = -19 ————-(ii)

Al sumar las ecuaciones (i) y (ii), obtenemos el punto de intersección P.

Ahora ponga el valor de y de la ec. (i) en la ec. (ii), obtenemos

x + 5(5x – 7) = -19 [usando la Ec. (i)]

⇒x + 25x – 35 = -19

⇒26x = 16

X = 8/13

Ahora ponga el valor de x en la ecuación (i), obtenemos

$y=5(\frac{8}{13})-7=\frac{40}{13}-7\\ ⇒y=\frac{40-91}{13}⇒y=\frac{-51}{13}$

Entonces, las coordenadas del punto P $=(\frac{8}{13},\frac{-51}{13})$

Y, la longitud de la altura de un paralelogramo,

$DP=\sqrt{(\frac{8}{13}+4)^2+(\frac{-51}{13}+3)^2}$

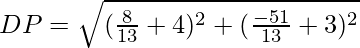
Ahora, usando la fórmula de la distancia, obtenemos

$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ ⇒DP=\sqrt{(\frac{60}{13})^2+(\frac{-12}{13})^2}\\ =\frac{1}{13}\sqrt{3600+144}\\ =\frac{1}{13}.\sqrt{3744}=\frac{12\sqrt{26}}{13}$

Por lo tanto, la longitud requerida de la altura de un paralelogramo es 12√26/13

Pregunta 33. A (6, 1), B (8, 2) y C (9, 4) son tres vértices de un paralelogramo ABCD. Si E es el punto medio de DC, encuentre el área de ∆ADE.

Solución:

Dado que ABCD es un paralelogramo, cuyos vértices son A (6,1), B (8,2) y C (9,4)

Supongamos que el cuarto vértice del paralelogramo sea D(x, y).

Ahora, como sabemos, las diagonales de un paralelogramo se bisecan entre sí.

entonces, Punto medio de BD = Punto medio de AC

⇒ $(\frac{8+x}{2},\frac{2+y}{2})=(\frac{6+9}{2},\frac{1+4}{2})$

⇒ $(\frac{8+x}{2},\frac{2+y}{2})=(\frac{15}{2},\frac{5}{2})\\ \frac{8+x}{2}=\frac{15}{2}$

⇒8+x=15⇒x=7

y $\frac{2+y}{2}=\frac{5}{2}$

⇒2 + y = 5 ⇒ y = 3

Entonces, el cuarto vértice de ||gm es D(7, 3)

Ahora, punto medio del lado DC $=(\frac{7+9}{2},\frac{3+4}{2})$

E = (8, 7/2)

Ahora encontramos el área de ∆ADE

= 1/2[6(3 – 7/2) + 7(7/2 – 1) + 8(1 – 3)]

= 1/2 [6 * (-1/2 + 7(5/2 + 8(-2))]

= 1/2 (-3 + 35/2 – 16)

= 1/2 (35/2 – 19)

= 1/2 (-3/2)

= -3/4 [Como sabemos que el área no puede ser negativa]

Por lo tanto, el área requerida ∆ADE es 3/4sq. unidades

Pregunta 34. Si D 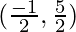$(\frac{-1}{2},\frac{5}{2})$ E (7, 3) y F 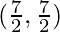$(\frac{7}{2},\frac{7}{2})$ son los puntos medios de los lados de ∆ABC, encuentra el área de ∆ABC.

Solución:

Dado que ABC es un triángulo, supongamos que los vértices del triángulo ABC son A(x ₁ , y ₁ ), B(x ₂ , y ₂ ) y C(x ₃ , y ₃ )

Y los puntos medios del lado BC, CA y AB son D(-1/2, 5/2), E(7, 3) y F(7/2, 7/2)

Dado que D(-1/2, 5/2) es el punto medio de BC.

Asi que, $\frac{x_2+x_3}{2}=-\frac{1}{2}$

y $\frac{y_2+y_3}{2}=\frac{5}{2}$

⇒x ₂ + x ₃ = -1 ————(i)

y y2 ₊ y3 ₌ 5

Como sabemos que E(7, 3) es el punto medio de CA.

Entonces, $\frac{x_3+x_1}{2}=7$ y $\frac{y_3+y_1}{2}=3$

⇒x ₃ + x ₁ = 14 ———–(iii)

y y ₃ + y ₁ = 6 ————(iv)

Además, F(7/2, 7/2) es el punto medio de AB $\frac{x_1+x_2}{2}=\frac{7}{2}$

y $\frac{y_1+y_2}{2}=\frac{7}{2}$

⇒x ₁ + x ₂ = 7 ————–(v)

y y ₁ + y ₂ = 7 —————-(vi)

Ahora, al sumar las ecuaciones (i), (ii) y (v), obtenemos

2(x1 + x2 ₊_x3 ) = ₂₀

x ₁ + x ₂ + x ₃ = 10 —————(vii)

Al restar la Ec. (i), (iii) y (v) de la ecuación. (vii), obtenemos

x1 = 11, x2 ₌_-4 , x3 = ₃

Al sumar las ecuaciones (ii), (iv) y (vi), obtenemos

2(y1 ₊_y2 + _y3 ) = 18

⇒y ₁ + y ₂ + y ₃ = 9 ————-(viii)

Al restar la Ec. (ii), (iv) y (vi) de la ecuación. (viii), obtenemos

y ₁ = 4, y ₂ = 3, y ₃ = 9

Por tanto, los vértices de ∆ABC son A(11, 4), B(-4, 3) y C(3, 2)

Área de ∆ABC = 1/2[x ₁ (y ₂ – y ₃ ) + (y ₃ – y ₁ )x ₂ + x ₃ (y ₁ – y ₂ )]

= 1/2[11(3 – 2) + (-4)(2 – 4) + 3(4 – 3)]

= 1/2[11 * 1 + (-4)(-2) + 3(1)]

= 1/2(11 + 8 + 3)

= 22/2 = 11

Por lo tanto, el área requerida de ∆ABC es 11 unidades cuadradas

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 10 Soluciones RD Sharma – Capítulo 14 Geometría de coordenadas – Ejercicio 14.5 | conjunto 3

Pregunta 23. Demuestra que los puntos (a, 0), (0, b) y (1, 1) son colineales si, 1/a + 1/b = 1.

Pregunta 24. El punto A divide el conjunto de P (-5, 1) y Q (3, 5) en la razón k : 1. Encuentra los dos valores de k para los cuales el área de ∆ABC donde B es (1, 5 ) y C (7, -2) es igual a 2 unidades.

Pregunta 25. El área de un triángulo es 5. Dos de sus vértices son (2, 1) y (3, -2). El tercer vértice se encuentra en y = x + 3. Encuentra el tercer vértice.

Pregunta 26. Se dan cuatro puntos A (6, 3), B (-3, 5), C (4, -2) y D (x, 3x) de tal forma que $\frac{△DBC}{△ABC}=\frac{1}{2}$ , ¿encontrar x?

Pregunta 27. Si tres puntos (x ₁ , y ₁ ), (x ₂ , y ₂ ), (x ₃ , y ₃ ) están en la misma recta, prueba que

$\frac{y_2-y_3}{x_2x_3}+\frac{y_3-y_1}{x_3x_1}+\frac{y_1-y_2}{x_1x_2}=0$

Pregunta 28. Halla el área de un paralelogramo ABCD si tres de sus vértices son A (2, 4), B (2 + √3, 5) y C (2, 6).

Pregunta 29. Encuentra el valor (s) de k para el cual los puntos (3k – 1, k – 2), (k, k – 7) y (k – 1, -k – 2) son colineales.

Pregunta 30. Si los puntos A (-1, -4), B (b, c) y C (5, -1) son colineales y 2b + c = 4, encuentra los valores de b y c.

Pregunta 31. Si los puntos A (-2, 1), B (a, b) y C (4, -1) son colineales y a – b = 1, encuentre los valores de a y 6.

Pregunta 32. Si los puntos A (1, -2), B (2, 3), C (a, 2) y D (-4, -3) forman un paralelogramo, encuentra el valor de a y la altura del paralelogramo tomando como base a AB.

Pregunta 33. A (6, 1), B (8, 2) y C (9, 4) son tres vértices de un paralelogramo ABCD. Si E es el punto medio de DC, encuentre el área de ∆ADE.

Pregunta 34. Si D $(\frac{-1}{2},\frac{5}{2})$ E (7, 3) y F $(\frac{7}{2},\frac{7}{2})$ son los puntos medios de los lados de ∆ABC, encuentra el área de ∆ABC.

Deja una respuesta Cancelar la respuesta

Pregunta 23. Demuestra que los puntos (a, 0), (0, b) y (1, 1) son colineales si, 1/a + 1/b = 1.

Pregunta 24. El punto A divide el conjunto de P (-5, 1) y Q (3, 5) en la razón k : 1. Encuentra los dos valores de k para los cuales el área de ∆ABC donde B es (1, 5 ) y C (7, -2) es igual a 2 unidades.

Pregunta 25. El área de un triángulo es 5. Dos de sus vértices son (2, 1) y (3, -2). El tercer vértice se encuentra en y = x + 3. Encuentra el tercer vértice.

Pregunta 26. Se dan cuatro puntos A (6, 3), B (-3, 5), C (4, -2) y D (x, 3x) de tal forma que , ¿encontrar x?

Pregunta 27. Si tres puntos (x 1 , y 1 ), (x 2 , y 2 ), (x 3 , y 3 ) están en la misma recta, prueba que

Pregunta 28. Halla el área de un paralelogramo ABCD si tres de sus vértices son A (2, 4), B (2 + √3, 5) y C (2, 6).

Pregunta 29. Encuentra el valor (s) de k para el cual los puntos (3k – 1, k – 2), (k, k – 7) y (k – 1, -k – 2) son colineales.

Pregunta 30. Si los puntos A (-1, -4), B (b, c) y C (5, -1) son colineales y 2b + c = 4, encuentra los valores de b y c.

Pregunta 31. Si los puntos A (-2, 1), B (a, b) y C (4, -1) son colineales y a – b = 1, encuentre los valores de a y 6.

Pregunta 32. Si los puntos A (1, -2), B (2, 3), C (a, 2) y D (-4, -3) forman un paralelogramo, encuentra el valor de a y la altura del paralelogramo tomando como base a AB.

Pregunta 33. A (6, 1), B (8, 2) y C (9, 4) son tres vértices de un paralelogramo ABCD. Si E es el punto medio de DC, encuentre el área de ∆ADE.

Pregunta 34. Si D E (7, 3) y F son los puntos medios de los lados de ∆ABC, encuentra el área de ∆ABC.

Deja una respuesta Cancelar la respuesta

Pregunta 26. Se dan cuatro puntos A (6, 3), B (-3, 5), C (4, -2) y D (x, 3x) de tal forma que $\frac{△DBC}{△ABC}=\frac{1}{2}$ , ¿encontrar x?

Pregunta 27. Si tres puntos (x ₁ , y ₁ ), (x ₂ , y ₂ ), (x ₃ , y ₃ ) están en la misma recta, prueba que

Pregunta 34. Si D $(\frac{-1}{2},\frac{5}{2})$ E (7, 3) y F $(\frac{7}{2},\frac{7}{2})$ son los puntos medios de los lados de ∆ABC, encuentra el área de ∆ABC.