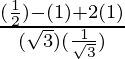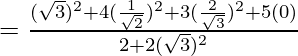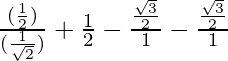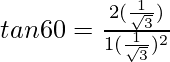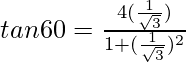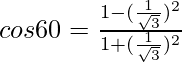Evalúe cada uno de los siguientes (14-19)
Pregunta 14. 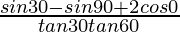
Solución:
Dado:
-(1)
Poniendo los valores de sen 30° = 1/2, tan 30° = 1/√3, tan 60° = √3, sen 90° = cos 0° = 1 en eq(1)
=
=
= 3/2
Pregunta 15. 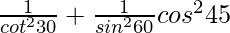
Solución:
Dado:
-(1)
= tan 2 30° + cos 2 60° − cos 2 45°
Poniendo los valores de cosec60° = 2/√3, cos45° = 1/√2, tan30° = 1/√3 en eq(1)
=
= 4/3 + 4/3 – 1/2
= (4 + 4)/3 – 1/2
= 8/3 – 1/2
= 13/6
Pregunta 16. 4(sen 4 30° + cos 2 60°) – 3(cos 2 45° – sen 2 90°) – sen 2 60°
Solución:
Dado: 4(sen 4 30° + cos 2 60°) – 3(cos 2 45° – sen 2 90°) – sen 2 60° -(1)
Poniendo los valores de cos45° = 1/√2, sen30° = cos30° = 1/2, sen60° = √3/2, sen90° = 1 en eq(1)
= 4((1/2) 4 + (1/2) 2 ) – 3((1/√2) 2 – (1) 2 ) – (√3/2) 2
= 4((1/16) + (1/4)) – 3((1/2) – 1) – (3/4)
= 4(5/16) – 3(-1/2) – 3/4
= 5/4 + 3/2 – 3/4
= (5 + 6 – 3)/4
= 8/4
= 2
Pregunta 17. 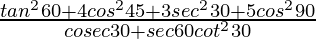
Solución:
Dado:
= 3 + 4(1/2) + 3(4/3)
= 3 + 2 + 4
= 9
Pregunta 18. Evaluar 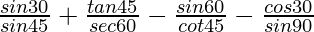
Solución:
Dado:
=
=
=
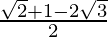
Pregunta 19. 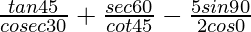
Solución:
Dado:
Como sabemos que
cosecθ = 1/senθ, cotθ = 1/tanθ
Ahora,
= tan45°sen30° + seg60°tan45° –
= 1 – 1/2 + 2 – 5/2
= (1 – 5)/2 + 2
= -2 + 2
= 0
Encuentre el valor de X en cada uno de los siguientes
Pregunta 20. 2sin3x = √3
Solución:
Dado,
2sen3x = √3
sen3x = √3/2
Como sabemos que,
sen60° = √3/2
Entonces, sen3x = sen60°
Ahora,
3x = 60°
x = 60°/3
x = 20°
Pregunta 21. 2sen x/2
Solución:
Dado
2senx/2 = 1 o senx/2 = 1/2
Sabemos sen30° = 1/2
Asi que,
senx/2 = sen30°
x/2 = 30°
x = 60°
Pregunta 22. √3senx = cosx
Solución:
Dado,
√3senx = cosx o senx/cosx = 1/√3
tan x = 1/√3
Sabemos tan30° = 1/√3
Asi que,
bronceado x = bronceado30°
x = 30°
Pregunta 23. tan x = sen45°cos45° + sen30°
Solución:
Dado: tan x = sen45°cos45° + sen30°
Poniendo los valores de sen 45° = cos 45° = 1/√2, sen 30° = 1/2
tan x = ((1/√2 × 1/√2) + 1/2)
tan x = (1/√2) 2 + 1/2
tan x = 1/2 + 1/2
bronceado x = 1
bronceado x = bronceado45°
Entonces, x = 45°
Pregunta 24. √3tan 2x = cos60° + sen45°cos45°
Solución:
Poniendo los valores de sin 45° = cos 45° = 1/√2, cos 60° = 1/2 en la ecuación dada
√3tan 2x = 1/2 + 1/√2 × 1/√2
√3tan 2x = 1/2 + (1/√2) 2
√3tan 2x = 1/2 + 1/2
tan 2x = 1/√3
bronceado 2x = bronceado30°
Entonces, x = 15°
Pregunta 25. cos 2x = cos60°cos30° + sen60°sen30°
Solución:
Dado: cos 2x = cos60°cos30° + sen60°sen30°
Poniendo los valores de sen 30° = cos 60° = 1/2, cos 30° = sen 60° = √3/2
porque 2x = 1/2 × √3/2 + √3/2 × 1/2
porque 2x = √3/4 + √3/4
cos 2x = √3/2
cos2x = cos30°
Entonces, x = 15°
Pregunta 26. Si θ = 30°, verifique que:
(i) tan2θ = 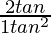
Solución:
Poniendo el valor de θ dado en la ecuación anterior
Obtenemos
√3 =
√3 =
√3 = √3
Por lo tanto probado
(ii) tan2θ = 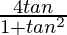
Solución:
Poniendo el valor de θ dado en la ecuación anterior
Obtenemos
√3 =
√3 =
√3 = √3
Por lo tanto probado
(iii) cos2θ = 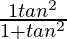
Solución:
Poniendo el valor de θ dado en la ecuación anterior
Obtenemos
1/2=(3-1)(3+1)
1/2 = 2/4 o 1/2
Por lo tanto probado
(iv) cos3θ = 4cos 3 θ − 3cosθ
Solución:
Poniendo el valor de θ dado en la ecuación anterior
Obtenemos
cos3(30°) = 4cos3 30 ° − 3cos30°
cos 90° = 4 cos 3 30° − 3 cos 30°
0 = 4(3√3/8) – 4(3√3/8)
0 = 3(√3/2) – 3(√3/2)
0 = 0
Por lo tanto probado
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA