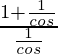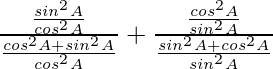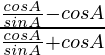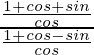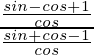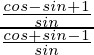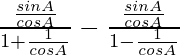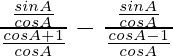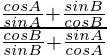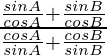Demostrar las siguientes identidades trigonométricas:
Pregunta 29. 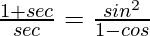
Solución:
Tenemos,
IZQ =
=
=
= 1 + cos θ
=
=
=
= lado derecho
Por lo tanto probado.
Pregunta 30. 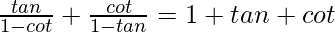
Solución:
Tenemos,
IZQ =
=
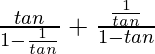
=
=
=
=
=
= 1 + tanθ + cotθ
= lado derecho
Por lo tanto probado.
Pregunta 31. seg 6 θ = tan 6 θ + 3 tan 2 θ seg 2 θ + 1
Solución:
Sabemos,
segundo 2 θ – bronceado 2 θ = 1
Al elevar al cubo ambos lados, obtenemos,
=> (seg 2 θ − tan 2 θ) 3 = 1
=> segundo 6 θ − bronceado 6 θ − 3 segundo 2 θ bronceado 2 θ(segundo 2 θ − bronceado 2 θ) = 1
=> seg 6 θ − bronceado 6 θ − 3 seg 2 θ bronceado 2 θ = 1
=> seg 6 θ = tan 6 θ + 3 seg 2 θ tan 2 θ + 1
Por lo tanto probado.
Pregunta 32. cosec 6 θ = cot 6 θ + 3cot 2 θ cosec 2 θ + 1
Solución:
Sabemos,
cosec 2 θ – cuna 2 θ = 1
Al cubo de ambos lados,
=> (coseg 2 θ − cuna 2 θ) 3 = 1
=> cosec 6 θ − cot 6 θ − 3 cosec 2 θ cot 2 θ (cosec 2 θ − cot 2 θ) = 1
=> cosec 6 θ − cuna 6 θ − 3 cosec 2 θ cuna 2 θ = 1
=> cosec 6 θ = cuna 6 θ + 3 cosec 2 θ cuna 2 θ + 1
Por lo tanto probado.
Pregunta 33. 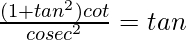
Solución:
Tenemos,
IZQ =
=
=
= sen θ/cos θ
= bronceado θ
= lado derecho
Por lo tanto probado.
Pregunta 34. 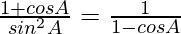
Solución:
Tenemos,
IZQ =
=
=
=
=
= lado derecho
Por lo tanto probado.
Pregunta 35. 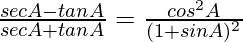
Solución:
Tenemos,
IZQ =
=
=
=
=
=
=
= lado derecho
Por lo tanto probado.
Pregunta 36. 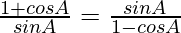
Solución:
Tenemos,
IZQ =
=
=
=
=
= lado derecho
Por lo tanto probado.
Pregunta 37. (i) 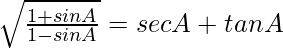
Solución:
Tenemos,
IZQ =
=
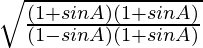
=
=
=
= seg A + tan A
= lado derecho
Por lo tanto probado.
(ii) 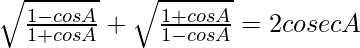
Solución:
Tenemos,
IZQ =
=
=
= 2 coseg A
= lado derecho
Por lo tanto probado.
Pregunta 38. (i) 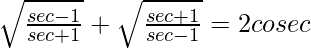
Solución:
Tenemos,
IZQ =
=
=
=
=
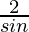
= 2 cosec θ
= lado derecho
Por lo tanto probado.
(ii) 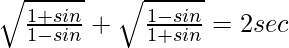
Solución:
Tenemos,
IZQ =
=
=
= 2 seg θ
= lado derecho
Por lo tanto probado.
(iii) 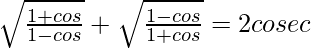
Solución:
Tenemos,
IZQ =
=
= 2 cosec θ
= lado derecho
Por lo tanto probado.
(iv) 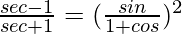
Solución:
Tenemos,
IZQ =
=
=
=
=
= lado derecho
Por lo tanto probado.
Pregunta 39. (seg A – tan A) 2 = 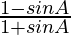
Solución:
Tenemos,
LHS = (seg A – tan A) 2
=
=
=
=
=
= lado derecho
Por lo tanto probado.
Pregunta 40. 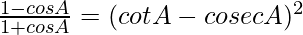
Solución:
Tenemos,
IZQ =
=
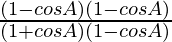
=
=
= (cosec A – cuna A) 2
= (cot A – cosec A) 2
= lado derecho
Por lo tanto probado.
Pregunta 41. 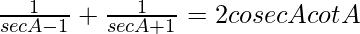
Solución:
Tenemos,
IZQ =
=
=
=
=
=
= 2 cosec A cuna A
= lado derecho
Por lo tanto probado.
Pregunta 42. 
Solución:
Tenemos,
IZQ =
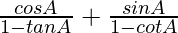
=
=
=
=
=
= sen A + cos A
= lado derecho
Por lo tanto probado.
Pregunta 43. 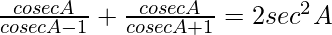
Solución:
Tenemos,
IZQ =
=
=
=
=
= 2 seg 2 A
= lado derecho
Por lo tanto probado.
Pregunta 44. 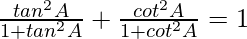
Solución:
Tenemos,
IZQ =
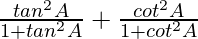
=
=
=
= 1
= lado derecho
Por lo tanto probado.
Pregunta 45. 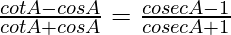
Solución:
Tenemos,
IZQ =
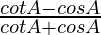
=
=
=
=
=
= lado derecho
Por lo tanto probado.
Pregunta 46. 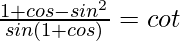
Solución:
Tenemos,
IZQ =
=
=
=
=
= cos θ/sen θ
= cuna θ
= lado derecho
Por lo tanto probado.
Pregunta 47. (i) 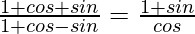
Solución:
Tenemos,
IZQ =
=
=
=
=
=
=
= sec θ + tan θ
= 1/cos θ + sen θ/cos θ
=
= lado derecho
Por lo tanto probado.
(ii) 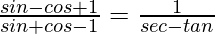
Solución:
Tenemos,
IZQ =
=
=
=
=
=
=
=
= lado derecho
Por lo tanto probado.
Pregunta 48. 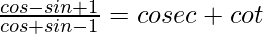
Solución:
Tenemos,
IZQ =
=
=
=
=
=
=
=
=
= cosec θ + cot θ
= lado derecho
Por lo tanto probado.
Pregunta 49. (sen θ + cos θ) (tan θ + cot θ) = sec θ + cosec θ
Solución:
Tenemos,
LHS = (sen θ + cos θ) (tan θ + cot θ)
= sen 2 θ/cos θ + cos θ + sen θ + cos 2 θ/sen θ
= sen θ (1 + tan θ) + (cos θ/tan θ) (1 + tan θ)
= (1 + tan θ) (sen θ + cos θ/tan θ)
=
=
= segundo θ + cosegundo θ
= lado derecho
Por lo tanto probado.
Pregunta 50. 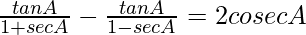
Solución:
Tenemos,
IZQ =
=
=
=
=
=
=
= 2/sen A
= 2 coseg A
= lado derecho
Por lo tanto probado.
Pregunta 51. 1 + 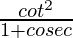 = cosec θ
= cosec θ
Solución:
Tenemos,
IZQ = 1 +
= 1 +
= 1+
= 1 + cosec θ − 1
= cosec θ
= lado derecho
Por lo tanto probado.
Pregunta 52. 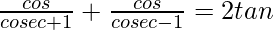
Solución:
Tenemos,
IZQ =
=
=
=
=
=
= 2 sen θ/cos θ
= 2 tan θ
= lado derecho
Por lo tanto probado.
Pregunta 53. (1 + tan 2 A) + (1 + 1/tan 2 A) = 1/(sen 2 A − sen 4 A)
Solución:
Tenemos,
LHS = (1 + tan 2 A) + (1 + 1/tan 2 A)
= (1 + sen 2 A/cos 2 A) + (1 + cos 2 A/sen 2 A)
= 1/cos 2 A + 1/sen 2 A
=
=
= 1/(sen 2 A − sen 4 A)
= lado derecho
Por lo tanto probado.
Pregunta 54. sen 2 A cos 2 B − cos 2 A sen 2 B = sen 2 A − sen 2 B
Solución:
Tenemos,
LHS = sen 2 A cos 2 B − cos 2 A sen 2 B
= sen 2 A (1 − sen 2 B) − sen 2 B (1 − sen 2 A)
= sen 2 A− sen 2 A sen 2 B − sen 2 B + sen 2 A sen 2 B
= sen 2 A − sen 2 B
= lado derecho
Por lo tanto Probado.
Pregunta 55. (i) 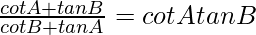
Solución:
Tenemos,
IZQ =
=
=
=
= cuna A tan B
= lado derecho
Por lo tanto probado.
(ii) 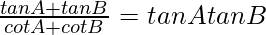
Solución:
Tenemos,
IZQ =
=
=
=
= bronceado A bronceado B
= lado derecho
Por lo tanto probado.
Pregunta 56. cot 2 A cosec 2 B − cot 2 B cosec 2 A = cot 2 A − cot 2 B
Solución:
Tenemos,
LHS = cuna 2 A cosec 2 B − cuna 2 B cosec 2 A
= cuna 2 A (1 + cuna 2 B) − cuna 2 B (1 + cuna 2 A)
= cuna 2 A + cuna 2 A cuna 2 B − cuna 2 B − cuna 2 B cuna 2 A
= cuna 2 A − cuna 2 B
= lado derecho
Por lo tanto probado.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA