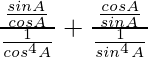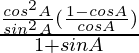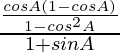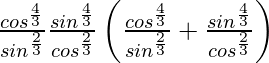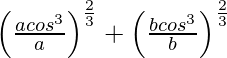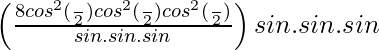Clase 10 Soluciones RD Sharma – Capítulo 6 Identidades trigonométricas – Ejercicio 6.1 | conjunto 3

Posted on by Rudeus Greyrat

Demostrar las siguientes identidades trigonométricas:

Pregunta 57. tan 2 A seg 2 B − seg 2 A tan 2 B = tan 2 A − tan 2 B

Solución:

Tenemos,

LHS = tan 2 A seg 2 B − seg 2 A tan 2 B

= tan 2 A (1 + tan 2 B) − tan 2 B (1+ tan 2 A)

= bronceado 2 A + bronceado 2 A bronceado 2 B − bronceado 2 B − bronceado 2 A bronceado 2 B  

= bronceado 2 A − bronceado 2 B  

= lado derecho

Por lo tanto probado.

Pregunta 58. Si x = a sec θ + b tan θ y y = a tan θ + b sec θ, Demuestre que x 2 − y 2 = a 2 − b 2 . 

Solución:

Tenemos,

IZQ = x 2 − y 2

= (un segundo θ + segundo bronceado θ) 2 − (un bronceado θ + segundo segundo θ) 2  

= a 2 seg 2 θ + b 2 tan 2 θ + 2ab seg θ tan θ − a 2 tan 2 θ − b 2 seg 2 θ – 2ab seg θ tan θ  

= un 2 segundos 2 θ + segundo 2 bronceado 2 θ – un 2 bronceado 2 θ – segundo 2 segundos 2 θ  

= un 2 segundos 2 θ – segundo 2 segundos 2 θ + segundo 2 bronceado 2 θ – un 2 bronceado 2 θ  

= segundo 2 θ (un 2 – segundo 2 ) + bronceado 2 θ ( segundo 2 – un 2 )  

= segundo 2 θ (un 2 – segundo 2 ) – bronceado 2 θ (un 2 – segundo 2 )  

= (seg 2 θ − bronceado 2 θ) (un 2 − segundo 2 ) 

= un 2 – segundo 2  

= lado derecho 

Por lo tanto probado.

Pregunta 59. Si 3 sen θ + 5 cos θ = 5, prueba que 5 sen θ – 3 cos θ = 3.

Solución:

Se nos da,

=> 3 sen θ + 5 cos θ = 5

=> 3 sen θ = 5 (1 − cos θ) 

=> 3 sen θ = \frac{5(1−cosθ)(1+cosθ)}{1+cosθ}

=> 3 sen θ = \frac{5(1−cos^2θ)}{1+cosθ}

=> 3 sen θ = \frac{5sin^2θ}{1+cosθ}

=> 3 (1 + cos θ) = 5 sen θ

=> 3 + 3 cos θ = 5 sen θ

=> 5 sen θ − 3 cos θ = 3

Por lo tanto probado.

Pregunta 60. Si cosec θ + cot θ = m y cosec θ – cot θ = n, demuestre que mn = 1.  

Solución:

Tenemos,

LHS = mn 

= (cosec θ + cot θ) (cosec θ – cot θ)  

= cosec 2 θ − cuna 2 θ  

= 1

= lado derecho 

Por lo tanto probado. 

Pregunta 61. Si T n = sen n θ + cos n θ, Demuestre que 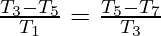 \frac{T_3-T_5}{T_1}=\frac{T_5-T_7}{T_3}.

Solución:

Tenemos,

IZQ = \frac{T_3-T_5}{T_1}

= \frac{(sin^3θ+cos^3θ)-(sin^5θ+cos^5θ)}{sinθ+cosθ}

= \frac{sin^3θ(1-sin^2θ)+cos^3θ(1-cos^2θ)}{sinθ+cosθ}

= \frac{sin^3θ(cos^2θ)+cos^3θ(sin^2θ)}{sinθ+cosθ}

= \frac{sin^2θcos^2θ(sinθ+cosθ)}{sinθ+cosθ}

= sen 2 θ cos 2 θ

Y RHS = \frac{T_5-T_7}{T_3}

= \frac{(sin^5θ+cos^5θ)-(sin^7θ+cos^7θ)}{sin^3θ+cos^3θ}

= \frac{sin^5θ(1-sin^2θ)+cos^5θ(1-cos^2θ)}{sin^3θ+cos^3θ}

= \frac{sin^5θ(cos^2θ)+cos^5θ(sin^2θ)}{sin^3θ+cos^3θ}

= \frac{sin^2θcos^2θ(sin^3θ+cos^3θ)}{sin^3θ+cos^3θ}

= sen 2 θ cos 2 θ

Por lo tanto, LHS = RHS

Por lo tanto probado.

Pregunta 62. 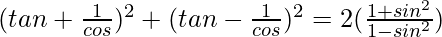(tanθ+\frac{1}{cosθ})^2+(tanθ-\frac{1}{cosθ})^2=2(\frac{1+sin^2θ}{1-sin^2θ})

Solución:

Tenemos,

IZQ = (tanθ+\frac{1}{cosθ})^2+(tanθ-\frac{1}{cosθ})^2

= (tan θ + sec θ) 2 + (tan θ – sec θ) 2

= tan 2 θ + seg 2 θ + 2 tan θ seg θ + tan 2 θ + seg 2 θ – 2 tan θ seg θ

= 2[tan 2 θ + sec 2 θ]

= 2\frac{sen^2θ}{cos^2θ}+\frac{1}{cos^2θ}

= 2\frac{1+sen^2θ}{cos^2θ}

= 2\frac{1+sen^2θ}{1-sen^2θ}

= lado derecho

Por lo tanto probado.

Pregunta 63. 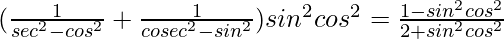(\frac{1}{sec^2θ-cos^2θ}+\frac{1}{cosec^2θ-sin^2θ})sin^2θcos^2θ=\frac{1-sin^2θcos^2θ}{2+sin^2θcos^2θ}

Solución:

Tenemos,

IZQ = (\frac{1}{sec^2θ-cos^2θ}+\frac{1}{cosec^2θ-sin^2θ})sin^2θcos^2θ

= (\frac{1}{\frac{1}{cos^2θ}-cos^2θ}+\frac{1}{\frac{1}{sin^2θ}-sin^2θ})sin^2θcos^2θ

= (\frac{cos^2θ}{1-cos^4θ}+\frac{sin^2θ}{1-sin^4θ})sin^2θcos^2θ

= (\frac{cos^2θ}{cos^2θ+sin^2θ-cos^4θ}+\frac{sin^2θ}{sin^2θ+cos^2θ-sin^4θ})sin^2θcos^2θ

= [\frac{cos^2θ}{cos^2θ(1-cos^2θ)+sin^2θ}+\frac{sin^2θ}{sin^2θ(1-sin^2θ)+cos^2θ}]sin^2θcos^2θ

= [\frac{cos^2θ}{sin^2θ(cos^2θ+1)}+\frac{sin^2θ}{cos^2θ(sin^2θ+1)}]sin^2θcos^2θ

= \left[\frac{cos^4θ+cos^4θsin^2θ+sin^4θ+sin^4θcos^2θ}{sin^2θcos^2θ(cos^2θ+1)(sin^2θ+1)}\right]sin^2θcos^2θ

= \frac{1-2sin^2θcos^2θ+sin^2θcos^2θ(cos^2θ+sin^2θ)}{1+cos^2θ+sin^2θ+cos^2θsin^2θ}

= \frac{1-sin^2θcos^2θ}{2+cos^2θsin^2θ}

= lado derecho

Por lo tanto probado.

Pregunta 64. (i) \left[\frac{1+sinθ-cosθ}{1+sinθ+cosθ}\right]^2=\frac{1-cosθ}{1+cosθ}

Solución:

Tenemos,

IZQ = \left[\frac{1+sinθ-cosθ}{1+sinθ+cosθ}\right]^2

= \left[\frac{(1+sinθ-cosθ)(1+sinθ-cosθ)}{(1+sinθ+cosθ)(1+sinθ-cosθ)}\right]^2

= \left[\frac{(1+sinθ-cosθ)^2}{(1+sinθ)^2-cos^2θ}\right]^2

= \left[\frac{1+sin^2θ+cos^2θ+2sinθ-2sinθcosθ-2cosθ}{1+sin^2θ+2sinθ-cos^2θ}\right]^2

= \left[\frac{2+2sinθ-2sinθcosθ-2cosθ}{2sin^2θ+2sinθ}\right]^2

= \left[\frac{2(1+sinθ)-2cosθ(sinθ+1)}{2sinθ(sinθ+1)}\right]^2

= \left[\frac{(1+sinθ)(2-2cosθ)}{2sinθ(sinθ+1)}\right]^2

= \left[\frac{2-2cosθ}{2sinθ}\right]^2

= \frac{(1-cosθ)(1-cosθ)}{sin^2θ}

= \frac{(1-cosθ)(1-cosθ)}{1-cos^2θ}

= \frac{(1-cosθ)(1-cosθ)}{(1+cosθ)(1-cosθ)}

= \frac{1-cosθ}{1+cosθ}

= lado derecho

Por lo tanto probado.

(ii) 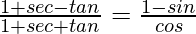\frac{1+secθ-tanθ}{1+secθ+tanθ}=\frac{1-sinθ}{cosθ}

Solución:

Tenemos,

IZQ = \frac{1+secθ-tanθ}{1+secθ+tanθ}

= \frac{(sec^2θ-tan^2θ)+secθ-tanθ}{1+secθ+tanθ}

= \frac{(secθ+tanθ)(secθ-tanθ)+(secθ-tanθ)}{1+secθ+tanθ}

= \frac{(secθ-tanθ)[1+secθ+tanθ]}{1+secθ+tanθ}

= segundo θ – bronceado θ

= 1/cos θ − sen θ/cos θ

= \frac{1-sinθ}{cosθ}

= lado derecho

Por lo tanto probado.

Pregunta 65. (sec A + tan A − 1) (sec A – tan A + 1) = 2 tan A 

Solución:

Tenemos,

LHS = (seg A + tan A − 1) (seg A – tan A + 1)

= [sec A + tan A − (sec A + tan A) (sec A – tan A)] [sec A – tan A + (sec A – tan A)(sec A + tan A)]

= (sec A + tan A) (1 − (sec A – tan A)) (sec A – tan A) (1 + (sec A + tan A))  

= (seg 2 A − tan 2 A) (1 – seg A + tan A) (1 + seg A + tan A) 

= (1 – seg A + tan A) (1 + seg A + tan A) 

= (1 – 1/cos A + sen A/cos A) (1 + 1/cos A + sen A/cos A)

= (\frac{cosA-1+sinA}{cosA})(\frac{cosA+1+sinA}{cosA})

= \frac{(cosA+sinA)^2-1}{cos^2A}

= \frac{cos^2A+sin^2A+2cosAsinA-1}{cos^2A}

= \frac{2cosAsinA}{cos^2A}

= sen A/cos A

= 2 tan A

= lado derecho

Por lo tanto probado.

Pregunta 66. (1 + cot A − cosec A)(1 + tan A + sec A) = 2 

Solución:

Tenemos,

LHS = (1 + cot A − cosec A)(1 + tan A + sec A)

= (1 + cos A/sen A − 1/sen A)(1 + sen A/cos A + 1/cos A)

= (\frac{sinA+cosA-1}{sinA})(\frac{cosA+sinA+1}{cosA})

= \frac{(sinA+cosA)^2-1}{sinAcosA}

= \frac{sin^2A+cos^2A+2sinAcosA-1}{sinAcosA}

= \frac{2sinAcosA}{sinAcosA}

= 2

= lado derecho

Por lo tanto probado.

Pregunta 67. (cosec θ – sec θ) (cot θ – tan θ) = (cosec θ + sec θ) (sec θ cosec θ − 2) 

Solución:

Tenemos,

LHS = (cosec θ – sec θ) (cot θ – tan θ)

= [\frac{1}{sinθ}-\frac{1}{cosθ}][\frac{cosθ}{sinθ}-\frac{sinθ}{cosθ}]

= [\frac{cosθ-sinθ}{sinθcosθ}][\frac{cos^2θ-sin^2θ}{sinθcosθ}]

= \left[\frac{(cosθ-sinθ)^2(cosθ+sinθ)}{sin^2θcos^2θ}\right]

Y RHS = (coseg θ + sec θ) (sec θ cosec θ − 2) 

= [\frac{1}{sinθ}+\frac{1}{cosθ}][(\frac{1}{cosθ})(\frac{1}{sinθ})-2]

= [\frac{sinθ+cosθ}{sinθcosθ}][\frac{1-2sinθcosθ}{sinθcosθ}]

= [\frac{sinθ+cosθ}{sinθcosθ}][\frac{sin^2θ+cos^2θ-2sinθcosθ}{sinθcosθ}]

= [\frac{sinθ+cosθ}{sinθcosθ}][\frac{(sinθ-cosθ)^2}{sinθcosθ}]

= \left[\frac{(cosθ-sinθ)^2(cosθ+sinθ)}{sin^2θcos^2θ}\right]

Por lo tanto, LHS = RHS

Por lo tanto probado.

Pregunta 68. \frac{cosAcosecA-sinAsecA}{cosA+sinA}=cosecA-secA

Solución:

Tenemos,

IZQ = \frac{cosAcosecA-sinAsecA}{cosA+sinA}

= \frac{\frac{cosA}{sinA}-\frac{sinA}{cosA}}{cosA+sinA}

= \frac{cos^2A-sin^2A}{cosAsinA}\left(\frac{1}{cosA+sinA}\right)

= \frac{cosA-sinA}{cosAsinA}

= cosec A − sec A

= lado derecho

Por lo tanto probado.

Pregunta 69. 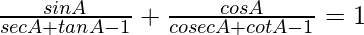\frac{sinA}{secA+tanA-1}+\frac{cosA}{cosecA+cotA-1}=1

Solución:

Tenemos,

IZQ = \frac{sinA}{secA+tanA-1}+\frac{cosA}{cosecA+cotA-1}

= \frac{sinA}{\frac{1+sinA-cosA}{cosA}}+\frac{cosA}{\frac{1+cosA-sinA}{sinA}}

= sinAcosA(\frac{1}{1+sinA-cosA}+\frac{1}{1+cosA-sinA})

= \frac{2sinAcosA}{(1+sinA-cosA)(1+cosA-sinA)}

= \frac{2sinAcosA}{cosA-sinA+sinA+sinAcosA-sin^2A-cosA-cos^2A+cosAsinA}

= \frac{2sinAcosA}{1-(sin^2A+cos^2A)+2sinAcosA}

= \frac{2sinAcosA}{2sinAcosA}

= 1

= lado derecho

Por lo tanto probado.

Pregunta 70. 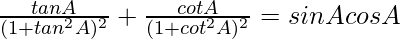\frac{tanA}{(1+tan^2A)^2}+\frac{cotA}{(1+cot^2A)^2}=sinAcosA

Solución:

Tenemos,

= \frac{tanA}{(1+tan^2A)^2}+\frac{cotA}{(1+cot^2A)^2}

= \frac{tanA}{sec^4A}+\frac{cotA}{cosec^4A}

= \frac{\frac{sinA}{cosA}}{\frac{1}{cos^4A}}+\frac{\frac{cosA}{sinA}}{\frac{1}{sin^4A}}

= sen A cos 3 A + cos A sen 3 A

= sen A cos A (sen 2 A + cos 2 A)

= sen A cos A

= lado derecho

Por lo tanto probado.

Pregunta 71. sec 4 A (1 − sen 4 A) – 2 tan 2 A = 1

Solución:

Tenemos,

LHS = sec 4 A (1 − sen 4 A) – 2 tan 2 A

= seg 4 A – tan 4 A – 2 tan 4 A

= (seg 2 A) 2 – tan 4 A – 2 tan 4 A  

= (1+ tan 2 A) 2 − tan 4 A − 2 tan 4 A

= 1 + bronceado 4 UN + 2 bronceado 2 UN − bronceado 4 UN − 2 bronceado 4 UN  

= 1

= lado derecho

Por lo tanto probado.

Pregunta 72. 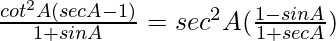\frac{cot^2A(secA-1)}{1+sinA}=sec^2A(\frac{1-sinA}{1+secA})

Solución:

Tenemos,

IZQ = \frac{cot^2A(secA-1)}{1+sinA}

= \frac{\frac{cos^2A}{sin^2A}(\frac{1-cosA}{cosA})}{1+sinA}

= \frac{\frac{cosA(1-cosA)}{1-cos^2A}}{1+sinA}

= \frac{cosA}{(1+sinA)(1+cosA)}

Y RHS = sec^2A(\frac{1-sinA}{1+secA})  

= \frac{1}{cos^2A}(\frac{1-sinA}{1+secA})

= \frac{cosA}{cos^2A}(\frac{1-sinA}{1+cosA})

= \frac{1}{cosA}(\frac{1-sinA}{1+cosA})

= \frac{1+sinA}{cosA(1+sinA)}(\frac{1-sinA}{1+cosA})

= \frac{1-sin^2A}{cosA(1+sinA)(1+cosA)}

= \frac{cos^2A}{cosA(1+sinA)(1+cosA)}

= \frac{cosA}{(1+sinA)(1+cosA)}

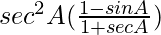
Por lo tanto, LHS = RHS

Por lo tanto probado.

Pregunta 73. (1 + cot A + tan A) (sen A – cos A) = sin A tan A – cos A cot A

Solución:

Tenemos,

LHS = (1 + cot A + tan A) (sen A – cos A)

= sen A – cos A + cot A sen A – cot A cos A + sen A tan A – tan A cos A

= sen A – cos A + cos A – cot A cos A + sen A tan A – sen A

= sen A tan A – cos A cot A

= lado derecho

Por lo tanto probado.

Pregunta 74. Si x cos θ/a + y sen θ/b = 1 y x cos θ/a – y sen θ/b = 1, entonces demuestre que x 2 /a 2 + y 2 /b 2 = 2.

Solución:

Tenemos,

X porque θ/a + y sen θ/b = 1 . . . . (1)

x porque θ/a – y sen θ/b = 1 . . . . (2)

Al elevar al cuadrado ambos lados de (1) y (2) y sumarlos obtenemos,

=> (x cos θ/a + y sen θ/b) 2 + (x cos θ/a – y sen θ/b) 2 = 1 + 1

=>  \frac{x^2cos^2θ}{a^2}+\frac{y^2sin^2θ}{b^2}+\frac{2xycosθsinθ}{ab}+\frac{x^2sin^2θ}{a^2}+\frac{y^2cos^2θ}{b^2}-\frac{2xycosθsinθ}{ab}  = 2

=>  cos^2θ(\frac{x^2}{a^2}+\frac{y^2}{b^2})+sin^2θ(\frac{x^2}{a^2}+\frac{y^2}{b^2})  = 2

=>  \frac{x^2}{a^2}+\frac{y^2}{b^2}  = 2

Por lo tanto probado.

Pregunta 75. Si cosec θ – sen θ = a 3 , sec θ – cos θ = b 3 , Demuestre que a 2 b 2 (a 2 + b 2 ) = 1. 

Solución:

Se nos da,

=> cosec θ – sen θ = a 3

=> 1/sen θ – sen θ = a 3

=> un 3 = \frac{1-sin^2θ}{sinθ}

=> un 3 = \frac{cos^2θ}{sinθ}

=> un = \frac{cos^\frac{2}{3}θ}{sin^\frac{1}{3}θ}

Al elevar al cuadrado ambos lados, obtenemos,

=> un 2 = \frac{cos^\frac{4}{3}θ}{sin^\frac{2}{3}θ}

También tenemos,

=> segundo θ – cos θ = segundo 3

=> 1/cos θ – cos θ = b 3

=> segundo 3 = \frac{1-cos^2θ}{cosθ}

=> segundo 3 = \frac{sin^2θ}{cosθ}

=> segundo = \frac{sin^\frac{2}{3}θ}{cos^\frac{1}{3}θ}

Al elevar al cuadrado ambos lados, obtenemos,

=> segundo 2 = \frac{sin^\frac{4}{3}θ}{cos^\frac{2}{3}θ}

Entonces, LHS = a 2 b 2 (a 2 + b 2 )

= \frac{cos^\frac{4}{3}θ}{sin^\frac{2}{3}θ}×\frac{sin^\frac{4}{3}θ}{cos^\frac{2}{3}θ}\left(\frac{cos^\frac{4}{3}θ}{sin^\frac{2}{3}θ}+\frac{sin^\frac{4}{3}θ}{cos^\frac{2}{3}θ}\right)

= cos^{\frac{2}{3}}θsin^{\frac{2}{3}}θ\left(\frac{1}{cos^{\frac{2}{3}}θsin^{\frac{2}{3}}θ}\right)

= 1

= lado derecho

Por lo tanto probado.

Pregunta 76. Si a cos 3 θ + 3a cos θ sen 2 θ = m y a sen 3 θ + 3a cos 2 θ sen θ = n, demuestre que  

(m + n)^{\frac{2}{3}} + (m − n)^{\frac{2}{3}} = 2a^{\frac{2}{3}}

Solución:

Se nos da,

m = a cos 3 θ + 3a cos θ sen 2 θ y n = a sen 3 θ + 3a cos 2 θ sen θ 

Entonces, LHS = (m + n)^{\frac{2}{3}} + (m − n)^{\frac{2}{3}}

= (a cos 3 θ + 3a cos θ sen 2 θ + a sen 3 θ + 3a cos 2 θ sen θ) 2/3 + (a cos 3 θ + 3a cos θ sen 2 θ – a sen 3 θ – 3a cos 2 θ sen θ) 2/3

= a 2/3 ((cos θ + sen θ) 3 ) 2/3 + a 2/3 ((cos θ − sen θ) 3 ) 2/3  

= a 2/3 [(cos θ + sen θ) 2 + (cos θ − sen θ) 2 ]

= a 2/3 [cos 2 θ + sen 2 θ + 2 sen θ cos θ + cos 2 θ + sen 2 θ − 2 sen θ cos θ]  

= 2 a 2/3

= lado derecho

Por lo tanto probado.

Pregunta 77. Si x = a cos 3 θ, y = b sen 3 θ, prueba que (x/a) 2/3 + (y/b) 2/3 = 1.

Solución:

Dado x = a cos 3 θ y y = b sen 3 θ.

Entonces, LHS = (x/a) 2/3 + (y/b) 2/3

= \left(\frac{acos^3θ}{a}\right)^{\frac{2}{3}}+\left(\frac{bcos^3θ}{b}\right)^{\frac{2}{3}}

= (cos 3 θ) 2/3 + (sen 3 θ) 2/3

= cos 2 θ + sen 2 θ

= 1

= lado derecho

Por lo tanto probado.

Pregunta 78. Si a cos θ + b sen θ = my a sen θ – b cos θ = n, Demuestre que a 2 + b 2 = m 2 + n 2 .  

Solución:

Tenemos,

lado derecho = metro 2 + norte 2 

= (a cos θ + b sen θ) 2 + (a sen θ – b cos θ) 2

= a 2 cos 2 θ + b 2 sen 2 θ + 2ab sen θ cos θ + a 2 sen 2 θ + b 2 cos 2 θ – 2ab sen θ cos θ

= a 2 cos 2 θ + a 2 cos 2 θ + b 2 sen 2 θ + b 2 cos 2 θ

= a 2 (sen 2 θ + cos 2 θ) + b 2 (sen 2 θ + cos 2 θ)

= un 2 + segundo 2 

= LHS

Por lo tanto probado.

Pregunta 79. Si cos A + cos 2 A = 1, Demostrar que sen 2 A + sen 4 A = 1.  

Solución:

Se nos da,

=> cos A + cos 2 A = 1

=> cos A = 1 − cos 2 A

=> cos A = sen 2 A . . . . (1)

Ahora, LHS = sen 2 A + sen 4 A

Usando (1), obtenemos,

= cos A + cos 2 A

= 1

= lado derecho

Por lo tanto probado.

Pregunta 80. Si cos θ + cos 2 θ = 1, demuestre que sen 12 θ + 3 sen 10 θ + 3 sen 8 θ + sen 6 θ + 2 sen 4 θ + 2 sen 2 θ − 2 = 1.

Solución:

Se nos da,

=> cos θ + cos 2 θ = 1  

=> cos θ = 1 − cos 2 θ  

=> porque θ = sen 2 θ . . . . (1)

Ahora, LHS = sen 12 θ + 3 sen 10 θ + 3 sen 8 θ + sen 6 θ + 2 sen 4 θ + 2 sen 2 θ − 2

= (sen 4 θ) 3 + 3 sen 4 θ sen 2 θ (sen 4 θ + sen 2 θ) + (sen 2 θ) 3 + 2(sen 2 θ) 2 + 2 sen 2 θ − 2

Usando (1), obtenemos,

= (sen 4 θ + sen 2 θ) 3 + 2cos 2 θ + 2 cos θ − 2  

= ((sen 2 θ) 2 + sen 2 θ) 3 + 2 cos 2 θ + 2 cos θ – 2

= (cos 2 θ + sen 2 θ) 3 + 2 cos 2 θ + 2 cos θ − 2  

= 1 + 2(cos 2 θ + sen 2 θ) − 2  

= 1 + 2(1) −2

= 1  

= lado derecho 

Por lo tanto probado.

Pregunta 81. Dado que: (1 + cos α)(1 + cos β)(1 + cos γ) = (1 – cos α)(1 – cos β)(1 – cos γ). Muestre que uno de los valores de cada miembro de esta igualdad es sen α sen β sen γ.  

Solución:

Tenemos,

= (1 + cos α)(1 + cos β)(1 + cos γ)

= 2 cos 2 (α/2).2 cos 2 (β/2).2 cos 2 (γ/2)

= \left(\frac{8cos^2(\frac{α}{2})cos^2(\frac{β}{2})cos^2(\frac{γ}{2})}{sinα.sinβ.sinγ}\right)sinα.sinβ.sinγ

= \left(\frac{8sin^2(\frac{α}{2})sin^2(\frac{β}{2})sin^2(\frac{γ}{2})}{2sin(\frac{α}{2})cos(\frac{α}{2}).sin(\frac{β}{2})cos(\frac{β}{2}).sin(\frac{γ}{2})cos(\frac{γ}{2})}\right)sinα.sinβ.sinγ

= sinα.sinβ.sinγ×tan\frac{α}{2}.tan\frac{β}{2}.tan\frac{γ}{2}

Por lo tanto, sen α sen β sen γ es el miembro de la igualdad.

Por lo tanto probado.

Pregunta 82. Si sen θ + cos θ = x, demuestre que sen 6 θ + cos 6 θ = 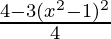 \frac{4-3(x^2-1)^2}{4}.

Solución:

Se nos da,

=> sen θ + cos θ = x

Al elevar al cuadrado ambos lados, obtenemos,

=> (sen θ + cos θ) 2 = x 2  

=> sen 2 θ + cos 2 θ + 2 sen θ cos θ = x 2

=> 2 sen θ cos θ = x 2 − 1

=> sen θ cos θ = (x 2 − 1)/2 . . . . (1)

Sabemos, 

=> sen 2 θ + cos 2 θ = 1 

Al cubo en ambos lados, obtenemos 

=> (sen 2 θ + cos 2 θ) 3 = 1 3

=> sen 6 θ + cos 6 θ + 3 sen 2 θ cos 2 θ (sen 2 θ + cos 2 θ) = 1

=> sen 6 θ + cos 6 θ = 1 – 3 sen 2 θ cos 2 θ

De (1), obtenemos,

=> sen 6 θ + cos 6 θ = 1 – \frac{3(x^2-1)^2}{4}

=> sen 6 θ + cos 6 θ = \frac{4-3(x^2-1)^2}{4}

Por lo tanto probado.

Pregunta 83. Si x = a sec θ cos ϕ, y = b sec θ sen ϕ y z = c tan ϕ, demuestre que, x 2 /a 2 + y 2 /b 2 − z 2 /c 2 = 1.

Solución:

Se nos da, x = a sec θ cos ϕ, y = b sec θ sin ϕ, z = c tan ϕ 

Al elevar al cuadrado x, y, z, obtenemos,

x 2 = un 2 seg 2 θ cos 2 ϕ o x 2 /a 2 = seg 2 θ cos 2 ϕ . . . . (1)

y 2 = segundo 2 seg 2 θ pecado 2 ϕ o y 2 /b 2 = segundo 2 θ pecado 2 ϕ . . . . (2)

z 2 = c 2 bronceado 2 ϕ o z 2 /c 2 = bronceado 2 ϕ . . . . (3)

Ahora LHS = x 2 /a 2 + y 2 /b 2 − z 2 /c 2  

Usando (1), (2) y (3), obtenemos,

= segundo 2 θ cos 2 ϕ + segundo 2 θ sen 2 ϕ − tan 2 ϕ  

= seg 2 θ (cos 2 ϕ + sen 2 ϕ) − tan 2 ϕ  

= segundo 2 θ (1) − bronceado 2 ϕ 

= segundo 2 θ – bronceado 2 θ 

= 1

= lado derecho

Por lo tanto probado.

Pregunta 84. Si sen θ + 2 cos θ. Demuestre que 2 sen θ – cos θ = 2. 

Solución:

Nos dan, sen θ + 2 cos θ = 1

Al elevar al cuadrado ambos lados, obtenemos,

=> (sen θ + 2 cos θ) 2 = 12  

=> sen 2 θ + 4 cos 2 θ + 4 sen θ cos θ = 1

=> 4 cos 2 θ + 4 sen θ cos θ = 1 – sen 2 θ  

=> 4 cos 2 θ + 4 sen θ cos θ – cos 2 θ = 0

=> 3 porque 2 θ + 4 pecado θ porque θ = 0 . . . . (1)

Tenemos, LHS = 2 sin θ – cos θ

Al cuadrar LHS, obtenemos,

= (2 sen θ – cos θ) 2  

= 4 sen 2 θ + cos 2 θ – 4 sen θ cos θ  

De (1), obtenemos,

= 4 sen 2 θ + cos 2 θ + 3 cos 2 θ

= 4 sen 2 θ + 4 cos 2 θ  

= 4(sen 2 θ + cos 2 θ)

= 4

Entonces tenemos,

=> (2 sen θ – cos θ) 2 = 4

=> 2 sen θ – cos θ = 2

Por lo tanto probado.

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *