Demostrar las siguientes identidades trigonométricas:
Pregunta 1. (1 – cos 2 A) cosec 2 A = 1
Solución:
Tenemos,
LHS = (1 – cos 2 A) cosec 2 A
Usando la identidad, sen 2 A + cos 2 A = 1, obtenemos,
= (sen 2 A) (coseg 2 A)
= sen 2 A × (1/sen 2 A)
= 1
= lado derecho
Por lo tanto probado.
Pregunta 2. (1 + cot 2 A) sen 2 A = 1
Solución:
Tenemos,
LHS = (1 + cuna 2 A) sen 2 A
Usando la identidad, cosec 2 A = 1 + cot 2 A, obtenemos,
= cosec 2 A sen 2 A
= (1/sen 2 A) × sen 2 A
= 1
= lado derecho
Por lo tanto probado.
Pregunta 3. tan 2 θ cos 2 θ = 1 − cos 2 θ
Solución:
Tenemos,
LHS = tan 2 θ cos 2 θ
= (sen 2 θ/cos 2 θ) (cos 2 θ)
= sen 2 θ
= 1 − cos 2 θ
= lado derecho
Por lo tanto probado.
Pregunta 4. cosec θ √(1 – cos 2 θ) = 1
Solución:
Tenemos,
LHS = cosec θ √(1 – cos 2 θ)
= cosec θ √(sen 2 θ)
= cosec θ sen θ
= (1/sen θ) (sen θ)
= 1
= lado derecho
Por lo tanto probado.
Pregunta 5. (seg 2 θ − 1)(coseg 2 θ − 1) = 1
Solución:
Tenemos,
LHS = (seg 2 θ − 1)(coseg 2 θ − 1)
Usando las identidades sec 2 θ − tan 2 θ = 1 y cosec 2 θ − cot 2 θ = 1, tenemos,
= bronceado 2 θ cuna 2 θ
= (tan 2 θ) (1/tan 2 θ)
= 1
= lado derecho
Por lo tanto probado.
Pregunta 6. tan θ + 1/tan θ = sec θ cosec θ
Solución:
Tenemos,
LHS = bronceado θ + 1/ bronceado θ
= (tan 2 θ + 1)/tan θ
= seg 2 θ/tan θ
=
=
= 1/sen θ cos θ
= seg θ cosec θ
= lado derecho
Por lo tanto probado.
Pregunta 7. cos θ/(1 – sen θ) = (1 + sen θ)/cos θ
Solución:
Tenemos,
LHS = cos θ/(1 – sen θ)
=
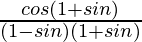
=
=
= (1 + sen θ)/cos θ
= lado derecho
Por lo tanto probado.
Pregunta 8. cos θ/(1 + sen θ) = (1 – sen θ)/cos θ
Solución:
Tenemos,
LHS = cos θ/(1 + sen θ)
=
=
=
= (1 – sen θ)/cos θ
= lado derecho
Por lo tanto probado.
Pregunta 9. cos 2 θ + 1/(1 + cot 2 θ) = 1
Solución:
Tenemos,
LHS = cos 2 θ + 1/(1 + cuna 2 θ)
= cos 2 θ + 1/(coseg 2 θ)
= cos 2 θ + sen 2 θ
= 1
= lado derecho
Por lo tanto probado.
Pregunta 10. sen 2 A + 1/(1 + tan 2 A) = 1
Solución:
Tenemos,
LHS = sen 2 A + 1/(1 + tan 2 A)
= sen 2 A + 1/(seg 2 A)
= sen 2 A + cos 2 A
= 1
= lado derecho
Por lo tanto probado.
Pregunta 11. 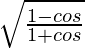 = cosec θ − cot θ
= cosec θ − cot θ
Solución:
Tenemos,
IZQ =
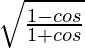
=
=
=
=
=
= cosec θ − cot θ
= lado derecho
Por lo tanto probado.
Pregunta 12. (1 – cos θ)/sen θ = sen θ/(1 + cos θ)
Solución:
Tenemos,
LHS = (1 – cos θ)/sen θ
=
=
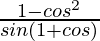
=
= sen θ/(1 + cos θ)
= lado derecho
Por lo tanto probado.
Pregunta 13. sen θ/(1 – cos θ) = cosec θ + cot θ
Solución:
Tenemos,
LHS = sen θ/(1 – cos θ)
=
=
=
=
=
= cosec θ + cot θ
= lado derecho
Por lo tanto probado.
Pregunta 14. (1 – sen θ)/(1 + sen θ) = (seg θ – tan θ) 2
Solución:
Tenemos,
LHS = (1 – sen θ)/(1 + sen θ)
=
=
=
=
=
= (seg θ – tan θ) 2
= lado derecho
Por lo tanto probado.
Pregunta 15. 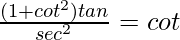
Solución:
Tenemos,
IZQ =
=
=
= cos θ/sen θ
= cuna θ
= lado derecho
Por lo tanto probado.
Pregunta 16. tan 2 θ − sen 2 θ = tan 2 θ sen 2 θ
Solución:
Tenemos,
LHS = tan 2 θ − sen 2 θ
= sen 2 θ/cos 2 θ − sen 2 θ
= sen 2 θ(1/cos 2 θ − 1)
=
= sen 2 θ (sen 2 θ/cos 2 θ)
= tan 2 θ sen 2 θ
= lado derecho
Por lo tanto probado.
Pregunta 17. (cosec θ + sen θ)(cosec θ – sen θ) = cot 2 θ + cos 2 θ
Solución:
Tenemos,
LHS = (coseg θ + sen θ)(coseg θ – sen θ)
= cosec 2 θ – sen 2 θ
= (1 + cuna 2 θ) – (1 – cos 2 θ)
= 1 + cuna 2 θ – 1 + cos 2 θ
= cuna 2 θ + cos 2 θ
= lado derecho
Por lo tanto probado.
Pregunta 18. (sec θ + cos θ) (sec θ – cos θ) = tan 2 θ + sen 2 θ
Solución:
Tenemos,
LHS = (sec θ + cos θ) (sec θ – cos θ)
= segundo 2 θ – cos 2 θ
= (1 + tan 2 θ) – (1 – sen 2 θ)
= 1 + tan 2 θ – 1 + sen 2 θ
= tan 2 θ + sen 2 θ
= lado derecho
Por lo tanto probado.
Pregunta 19. sec A(1 – sin A) (sec A + tan A) = 1
Solución:
Tenemos,
LHS = sec A(1 – sen A) (sec A + tan A)
=
=
=
= 1
= lado derecho
Por lo tanto probado.
Pregunta 20. (cosec A – sen A)(sec A – cos A)(tan A + cot A) = 1
Solución:
Tenemos,
LHS = (cosec A – sin A)(sec A – cos A)(tan A + cot A)
=
=
=
= 1
= lado derecho
Por lo tanto probado.
Pregunta 21. (1 + tan 2 θ)(1 – sen θ)(1 + sen θ) = 1
Solución:
Tenemos,
LHS = (1 + tan 2 θ)(1 – sen θ)(1 + sen θ)
= (seg 2 θ) (1 – sen 2 θ)
= (seg 2 θ) (cos 2 θ)
= 1
= lado derecho
Por lo tanto probado.
Pregunta 22. sen 2 A cot 2 A + cos 2 A tan 2 A = 1
Solución:
Tenemos,
LHS = sen 2 A cot 2 A + cos 2 A tan 2 A
= sen 2 A (cos 2 A/sen 2 A) + cos 2 A (sen 2 A/cos 2 A)
= cos 2 A + sen 2 A
= 1
= lado derecho
Por lo tanto probado.
Pregunta 23.
(i) cot θ – tan θ = 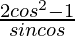
Solución:
Tenemos,
LHS = cuna θ – bronceado θ
= cos θ/sen θ – sen θ/cos θ
=
=
=
=
= lado derecho
Por lo tanto probado.
(ii) tan θ – cot θ = 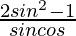
Solución:
Tenemos,
LHS = tan θ – cuna θ
= sen θ/cos θ – cos θ/sen θ
=
=
=
=
= lado derecho
Por lo tanto probado.
Pregunta 24. (cos 2 θ/sen θ) – cosec θ + sen θ = 0
Solución:
Tenemos,
LHS = (cos 2 θ/sen θ) – cosec θ + sen θ
=
=
=
= 0
= lado derecho
Por lo tanto probado.
Pregunta 25. 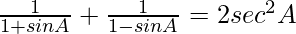
Solución:
Tenemos,
IZQ =
=
=
=
= 2 seg 2 A
= lado derecho
Por lo tanto probado.
Pregunta 26. 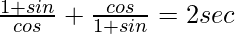
Solución:
Tenemos,
IZQ =
=
=
=
=
= 2 seg θ
= lado derecho
Por lo tanto probado.
Pregunta 27. 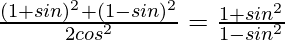
Solución:
Tenemos,
IZQ =
=
=
=
= lado derecho
Por lo tanto probado.
Pregunta 28. 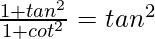
Solución:
Tenemos,
IZQ =
= segundo 2 θ/coseg 2 θ
=
= tan 2 θ
= lado derecho
Por lo tanto probado.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA