Pregunta 14. Encuentra la media de la siguiente distribución de frecuencia:
| Intervalo de clases: | 25 – 29 | 30 – 34 | 35 – 39 | 40 – 44 | 45 – 49 | 50 – 54 | 55 – 59 |
| Frecuencia: | 14 | 22 | dieciséis | 6 | 5 | 3 | 4 |
Solución:
Consideremos la media asumida (A) = 42
Intervalo de clases Valor medio x i re yo = x yo – 42 tu yo = (x yo – 42)/5 yo _ si yo tu yo 25 – 29 27 -15 -3 14 -42 30 – 34 32 -10 -2 22 -44 35 – 39 37 -5 -1 dieciséis -dieciséis 40 – 44 42 0 0 6 0 45 – 49 47 5 1 5 5 50 – 54 52 10 2 3 6 55 – 59 57 15 3 4 12 norte = 70 Σ F yo tu yo = -79 De la tabla se ve que,
A = 42 y h = 5
Media = A + hx (Σf i u i /N)
= 42 + 5 x (-79/70)
= 42 – 79/14
= 42 – 5.643
= 36.357
Pregunta 15. Para la siguiente distribución, calcule la media utilizando todos los métodos adecuados:
| Tamaño del artículo: | 1 – 4 | 4 – 9 | 9 – 16 | 16 – 20 |
| Frecuencia: | 6 | 12 | 26 | 20 |
Solución:
Por método directo
Intervalo de clases Valor medio x i Frecuencia fi arreglar yo x yo 1 – 4 2.5 6 15 4 – 9 6.5 12 18 9 – 16 12.5 26 325 16 – 27 21.5 20 430 norte = 64 Suma = 848 Media = (suma/N) + A
= 848/64
= 13,25
Asumiendo el método de la media
Sea la media supuesta (A) = 65
Intervalo de clases Valor medio x i tu yo = (x yo – A) = x yo – 65 Frecuencia fi si yo tu yo 1 – 4 2.5 -4 6 -25 4 – 9 6.5 0 12 0 9 – 16 12.5 6 26 196 16 – 27 21.5 15 20 300 norte = 64 Suma = 432 Media = A + suma/N
= 6,5 + 6,75
= 13,25
Pregunta 16. La observación semanal del índice del costo de vida en cierta ciudad para el año 2004 – 2005 se presenta a continuación. Calcule el costo semanal del índice de vida.
| índice de costo de vida | Numero de estudiantes | índice de costo de vida | Numero de estudiantes |
| 1400 – 1500 | 5 | 1700 – 1800 | 9 |
| 1500 – 1600 | 10 | 1800 – 1900 | 6 |
| 1600 – 1700 | 20 | 1900 – 2000 | 2 |
Solución:
Sea la media supuesta (A) = 1650
Intervalo de clases Valor medio x i re yo = x yo – A = x yo – 1650 Frecuencia fi si yo tu yo 1400 – 1500 1450 -200 -2 5 -10 1500 – 1600 1550 -100 -1 10 -10 1600 – 1700 1650 0 0 20 0 1700 – 1800 1750 100 1 9 9 1800 – 1900 1850 200 2 6 12 1900 – 2000 1950 300 3 2 6 norte = 52 Suma = 7 Tenemos
A = 16, h = 100
Media = A + h (suma/N)
= 1650 + (175/13)
= 21625/13
= 1663.46
Pregunta 17. La siguiente tabla muestra las calificaciones obtenidas por 140 estudiantes en un examen de un determinado trabajo:
| Marcas: | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Numero de estudiantes: | 20 | 24 | 40 | 36 | 20 |
Calcule las calificaciones promedio utilizando los tres métodos: método directo, desviación media supuesta y método abreviado.
Solución:
(i) Método directo:
Intervalo de clases Valor medio x i Frecuencia fi arreglar yo x yo 0 – 10 5 20 100 10 – 20 15 24 360 20 – 30 25 40 1000 30 – 40 35 36 1260 40 – 50 45 20 900 norte = 140 Suma = 3620 Media = suma/N
= 3620/140
= 25.857
(ii) Método medio asumido:
Sea la media asumida = 25
Media = A + (suma/N)
Intervalo de clases Valor medio x i tu yo = (x yo – A) Frecuencia fi si yo tu yo 0 – 10 5 -20 20 -400 10 – 20 15 -10 24 -240 20 – 30 25 0 40 0 30 – 40 35 10 36 360 40 – 50 45 20 20 400 norte = 140 Suma = 120 Media = A + (suma/N)
= 25 + (120/140)
= 25 + 0,857
= 25.857
(iii) Método de desviación de paso:
Sea la media supuesta (A) = 25
Intervalo de clases Valor medio x i re yo = x yo – A = x yo – 25 Frecuencia fi si yo tu yo 0 – 10 5 -20 -2 20 -40 10 – 20 15 -10 -1 24 -24 20 – 30 25 0 0 40 0 30 – 40 35 10 1 36 36 40 – 50 45 20 2 20 40 norte = 140 Suma = 12 Media = A + h(suma/N)
= 25 + 10(12/140)
= 25 + 0,857
= 25.857
Pregunta 18. La media de la siguiente distribución de frecuencias es 62,8 y la suma de todas las frecuencias es 50. Calcule la frecuencia perdida f 1 y f 2 .
| Clase: | 0 – 20 | 20 – 40 | 40 – 60 | 60 – 80 | 80 – 100 | 100 – 120 |
| Frecuencia: | 5 | F 1 | 10 | F 2 | 7 | 8 |
Solución:
Intervalo de clases Valor medio x i Frecuencia fi arreglar yo x yo 0 – 20 10 5 50 20 – 40 30 yo _ 30f yo 40 – 60 50 10 500 60 – 80 70 F 2 70f 2 80 – 100 90 7 630 100 – 120 110 8 880 norte = 50 Suma = 30f 1 + 70f 2 + 2060 Dado,
Suma de frecuencia = 50
5 + f 1 + 10 + f 2 + 7 + 8 = 50
f 1 + f 2 = 20
3f 1 + 3f 2 = 60 —(1) [Multiplica ambos lados por 3]
y media = 62.8
Suma/N = 62,8
(30f 1 + 70f 2 + 2060)/50 = 62,8
30f 1 + 70f 2 = 3140 – 2060
30f 1 + 70f 2 = 1080
3f 1 + 7f 2 = 108 —(2) [dividirlo por 10]
Reste la ecuación (1) de la ecuación (2)
3f 1 + 7f 2 – 3f 1 – 3f 2 = 108 – 60
4f 2 = 48
f 2 = 12
Ponga el valor de f 2 en la ecuación (1)
3f 1 + 3(12) = 60
f 1 = 24/3 = 8
f 1 = 8, f 2 = 12
Pregunta 19. La siguiente distribución muestra la asignación de bolsillo diaria que se les da a los niños de un edificio de varios pisos. La asignación de bolsillo promedio es de Rs 18.00. Averigüe la frecuencia que falta.
| Intervalo de clases: | 11 – 13 | 13 – 15 | 15 – 17 | 17 – 19 | 19 – 21 | 21 – 23 | 23 – 25 |
| Frecuencia: | 7 | 6 | 9 | 13 | – | 5 | 4 |
Solución:
Dada la media = 18,
Sea la frecuencia faltante v
Intervalo de clases Intervalo medio x i Frecuencia fi arreglar yo x yo 11 – 13 12 7 84 13 – 15 14 6 88 15 – 17 dieciséis 9 144 17 – 19 18 13 234 19 – 21 20 X 20x 21 – 23 22 5 110 23 – 25 14 4 56 norte = 44 + x Suma = 752 + 20x Media = suma/N
18 = 752 + 20×44 + x
792 + 18x = 752 + 20x
2x = 40
X = 20
Pregunta 20. Si la media de la siguiente distribución es 27. Calcula el valor de p.
| Clase: | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Frecuencia: | 8 | PAGS | 12 | 13 | 10 |
Solución:
Intervalo de clases Valor medio x i Frecuencia fi arreglar yo x yo 0 – 10 5 8 40 10 – 20 15 PAGS 152 20 – 30 25 12 300 30 – 40 35 13 455 40 – 50 45 dieciséis 450 norte = 43 + pag Suma = 1245 + 15p Media dada = 27
Media = suma/N
1245 + 15p43 + p
= 27
1245 + 15p = 1161 + 27p
12p = 84
PAG = 7
Pregunta 21. En un mercado minorista, los vendedores de frutas vendían mangos guardados en cajas de embalaje. Estas cajas contienen un número variable de mangos. La siguiente fue la distribución de los mangos según el número de cajas.
| Número de mangos: | 50 – 52 | 53 – 55 | 56 – 58 | 59 – 61 | 62 – 64 |
| Número de cajas: | 15 | 110 | 135 | 115 | 25 |
Encuentre la cantidad media de mangos guardados en la caja de embalaje. ¿Qué método para encontrar la media elegiste?
Solución:
Número de mangos Número de cajas 50 – 52 15 53 – 55 110 56 – 58 135 59 – 61 115 62 – 64 25 Podemos observar que las clases internas no son continuas.
Hay una brecha entre dos intervalos de clase. Así que tenemos que sumar ½ del límite de clase inferior a cada intervalo y la marca de clase (xi ) se puede obtener usando la relación
x i = límite superior + límite de clase inferior2
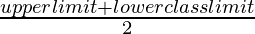
Tamaño de clase (h) de estos datos = 3
Ahora tomando 57 como media asumida (a) podemos calcular d i , u i , f i u i de la siguiente manera
Intervalo de clases Frecuencia fi Valores medios x i re yo = x yo – A = x yo – 25 si yo tu yo 49,5 – 52,5 15 51 -6 -2 -30 52,5 – 55,5 110 54 -3 -1 -110 55,5 – 58,5 135 57 0 0 0 58,5 – 61,5 115 60 3 1 115 61,5 – 64,5 25 63 6 2 50 Total norte = 400 Suma = 25 Ahora tenemos N
Suma = 25
Media = A +h (suma/N)
= 57 + 3 (45/400)
= 57 + 3/16
= 57 + 0,1875
= 57,19
Claramente, el número medio de mangos guardados en la caja de empaque es 57.19
Pregunta 22. La siguiente tabla muestra el gasto diario en alimentos de 25 hogares en una localidad
| Gasto diario (en Rs): | 100 – 150 | 150 – 200 | 200 – 250 | 250 – 300 | 300 – 350 |
| Número de hogares: | 4 | 5 | 12 | 2 | 2 |
Encuentre el gasto medio diario en alimentos mediante un método adecuado.
Solución:
Podemos calcular la nota de clase (xi ) para cada intervalo usando la relación
x i = límite superior + límite de clase inferior2
Tamaño de la clase = 50
Ahora, tomando 225 como media supuesta (x i ) podemos calcular d i , u i , f i u i de la siguiente manera
Gasto diario Frecuencia f 1 Valor medio x i re yo = x yo – 225 si yo tu yo 100 – 150 4 125 -100 -2 -8 150 – 200 5 175 -50 -1 -5 200 – 250 12 225 0 0 0 250 – 300 2 275 50 1 2 300 – 350 2 325 100 2 4 norte = 25 Suma = -7 Ahora podemos observar que
norte = 25
Suma = -7
225 + 50 (-7/25)
225 – 14 = 211
Entonces, el gasto diario promedio en alimentos es Rs 211
Pregunta 23. Para saber la concentración de SO 2 en el aire (en partes por millón, es decir, ppm) se recolectaron datos para localidades de 30 localidades en una determinada ciudad y se presentan a continuación:
| Concentración de SO 2 (en ppm) | Frecuencia |
| 0,00 – 0,04 | 4 |
| 0,04 – 0,08 | 9 |
| 0,08 – 0,12 | 9 |
| 0,12 – 0,16 | 2 |
| 0,16 – 0,20 | 4 |
| 0,20 – 0,24 | 2 |
Encuentre la concentración media de SO 2 en el aire
Solución:
Podemos encontrar notas de clase para cada intervalo usando la relación
x = límite superior + límite de clase inferior2x =
Tamaño de clase de estos datos = 0.04
Ahora tomando 0.04 media supuesta (x i ) podemos calcular d i , u i , f i u i de la siguiente manera
Concentración de SO 2 Frecuencia f 1 Intervalo de clase x i` re yo = x yo – 0.14 tu yo si yo tu yo 0,00 – 0,04 4 0.02 -0.12 -3 -12 0,04 – 0,08 9 0.06 -0.08 -2 -18 0,08 – 0,12 9 0.10 -0.04 -1 -9 0,12 – 0,16 2 0.14 0 0 0 0,16 – 0,20 4 0.18 0.04 1 4 0,20 – 0,24 2 0.22 0.08 2 4 Total norte = 30 Suma = -31 De la tabla podemos observar que
norte = 30
Suma = -31
= 0,14 + (0,04)(-31/30)
= 0,099 ppm
Entonces, la concentración media de SO 2 en el aire es de 0,099 ppm.
Pregunta 24. Un maestro de clase tiene el siguiente registro de ausencia de 40 estudiantes de una clase durante todo el período. Encuentre el número medio de días que un estudiante estuvo ausente.
| Número de días: | 0 – 6 | 6 – 10 | 10 – 14 | 14 – 20 | 20 – 28 | 28 – 38 | 38 – 40 |
| Numero de estudiantes: | 11 | 10 | 7 | 4 | 4 | 3 | 1 |
Solución:
Podemos encontrar la marca de clase de cada intervalo usando la relación
x = límite superior + límite de clase inferior2x =
Ahora, tomando 16 como media asumida (a) podemos
Calcular d i y f i d i de la siguiente manera
Número de días Número de estudiantes f i X yo d = x yo + 10 si yo si yo 0 – 6 11 3 -13 -143 6 – 10 10 8 -8 -280 10 – 14 7 12 -4 -28 14 – 20 7 dieciséis 0 0 20 – 28 8 24 8 32 28 – 36 3 33 17 51 30 – 40 1 39 23 23 Total norte = 40 Suma = -145 Ahora podemos observar que
norte = 40
Suma = -145
= 16 + (-145/40)
= 16 – 3.625
= 12,38
Por lo tanto, el número medio de días es 12,38 días en los que el estudiante estuvo ausente.
Pregunta 25. La siguiente tabla da la tasa de alfabetización (en porcentaje) de 35 ciudades. Hallar la tasa media de alfabetización.
| Tasa de alfabetización (en %): | 45 – 55 | 55 – 65 | 65 – 75 | 75 – 85 | 85 – 95 |
| Número de ciudades: | 3 | 10 | 11 | 8 | 3 |
Solución:
Podemos encontrar marcas de clase usando la relación
x = límite superior + límite de clase inferior2x =
Tamaño de la clase (h) para estos datos = 10
Ahora tomando 70 como media supuesta (a) incorrecta
Calcular d i , u i , f i u i de la siguiente manera
Tasa de alfabetización (en %) Número de ciudades (f i ) Valor medio x i re yo = x yo – 70 tu yo = re yo – 50 si yo tu yo 45 – 55 3 50 -20 -20 -6 55 – 65 10 60 -10 -1 -10 65 – 75 11 70 0 0 0 75 – 85 8 80 10 1 8 85 – 95 3 90 20 2 6 Total norte = 35 Suma = -2 Ahora podemos observar que
norte = 35
Suma = -2
= 70 + (-2/35)
= 70 – 4/7
= 70 – 0,57
= 69,43
Entonces, la tasa media de alfabetización es 69.43%
Pregunta 21. En un mercado minorista, los vendedores de frutas vendían mangos guardados en cajas de embalaje. Estas cajas contienen un número variable de mangos. La siguiente fue la distribución de los mangos según el número de cajas.
| Número de mangos: | 50 – 52 | 53 – 55 | 56 – 58 | 59 – 61 | 62 – 64 |
| Número de cajas: | 15 | 110 | 135 | 115 | 25 |
Encuentre la cantidad media de mangos guardados en la caja de embalaje. ¿Qué método para encontrar la media elegiste?
Solución:
Número de mangos Número de cajas 50 – 52 15 53 – 55 110 56 – 58 135 59 – 61 115 62 – 64 25 Podemos observar que las clases internas no son continuas.
Hay una brecha entre dos intervalos de clase. Así que tenemos que sumar ½ del límite de clase inferior a cada intervalo y la marca de clase (xi ) se puede obtener usando la relación
x i = límite superior + límite de clase inferior2
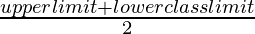
Tamaño de clase (h) de estos datos = 3
Ahora tomando 57 como media asumida (a) podemos calcular d i , u i , f i u i de la siguiente manera
Intervalo de clases Frecuencia fi Valores medios x i re yo = x yo – A = x yo – 25 si yo tu yo 49,5 – 52,5 15 51 -6 -2 -30 52,5 – 55,5 110 54 -3 -1 -110 55,5 – 58,5 135 57 0 0 0 58,5 – 61,5 115 60 3 1 115 61,5 – 64,5 25 63 6 2 50 Total norte = 400 Suma = 25 Ahora tenemos N
Suma = 25
Media = A +h (suma/N)
= 57 + 3 (45/400)
= 57 + 3/16
= 57 + 0,1875
= 57,19
Claramente, el número medio de mangos guardados en la caja de empaque es 57.19
Pregunta 22. La siguiente tabla muestra el gasto diario en alimentos de 25 hogares en una localidad
| Gasto diario (en Rs): | 100 – 150 | 150 – 200 | 200 – 250 | 250 – 300 | 300 – 350 |
| Número de hogares: | 4 | 5 | 12 | 2 | 2 |
Encuentre el gasto medio diario en alimentos mediante un método adecuado.
Solución:
Podemos calcular la nota de clase (xi ) para cada intervalo usando la relación
x i = límite superior + límite de clase inferior2
Tamaño de la clase = 50
Ahora, tomando 225 como media supuesta (x i ) podemos calcular d i , u i , f i u i de la siguiente manera
Gasto diario Frecuencia f 1 Valor medio x i re yo = x yo – 225 si yo tu yo 100 – 150 4 125 -100 -2 -8 150 – 200 5 175 -50 -1 -5 200 – 250 12 225 0 0 0 250 – 300 2 275 50 1 2 300 – 350 2 325 100 2 4 norte = 25 Suma = -7 Ahora podemos observar que
norte = 25
Suma = -7
225 + 50 (-7/25)
225 – 14 = 211
Entonces, el gasto diario promedio en alimentos es Rs 211
Pregunta 23. Para saber la concentración de SO 2 en el aire (en partes por millón, es decir, ppm) se recolectaron datos para localidades de 30 localidades en una determinada ciudad y se presentan a continuación:
| Concentración de SO 2 (en ppm) | Frecuencia |
| 0,00 – 0,04 | 4 |
| 0,04 – 0,08 | 9 |
| 0,08 – 0,12 | 9 |
| 0,12 – 0,16 | 2 |
| 0,16 – 0,20 | 4 |
| 0,20 – 0,24 | 2 |
Encuentre la concentración media de SO 2 en el aire
Solución:
Podemos encontrar notas de clase para cada intervalo usando la relación
x = límite superior + límite de clase inferior2x =
Tamaño de clase de estos datos = 0.04
Ahora tomando 0.04 media supuesta (x i ) podemos calcular d i , u i , f i u i de la siguiente manera
Concentración de SO 2 Frecuencia f 1 Intervalo de clase x i` re yo = x yo – 0.14 tu yo si yo tu yo 0,00 – 0,04 4 0.02 -0.12 -3 -12 0,04 – 0,08 9 0.06 -0.08 -2 -18 0,08 – 0,12 9 0.10 -0.04 -1 -9 0,12 – 0,16 2 0.14 0 0 0 0,16 – 0,20 4 0.18 0.04 1 4 0,20 – 0,24 2 0.22 0.08 2 4 Total norte = 30 Suma = -31 De la tabla podemos observar que
norte = 30
Suma = -31
= 0,14 + (0,04)(-31/30)
= 0,099 ppm
Entonces, la concentración media de SO 2 en el aire es de 0,099 ppm.
Pregunta 24. Un maestro de clase tiene el siguiente registro de ausencia de 40 estudiantes de una clase durante todo el período. Encuentre el número medio de días que un estudiante estuvo ausente.
| Número de días: | 0 – 6 | 6 – 10 | 10 – 14 | 14 – 20 | 20 – 28 | 28 – 38 | 38 – 40 |
| Numero de estudiantes: | 11 | 10 | 7 | 4 | 4 | 3 | 1 |
Solución:
Podemos encontrar la marca de clase de cada intervalo usando la relación
x = límite superior + límite de clase inferior2x =
Ahora, tomando 16 como media asumida (a) podemos
Calcular d i y f i d i de la siguiente manera
Número de días Número de estudiantes f i X yo d = x yo + 10 si yo si yo 0 – 6 11 3 -13 -143 6 – 10 10 8 -8 -280 10 – 14 7 12 -4 -28 14 – 20 7 dieciséis 0 0 20 – 28 8 24 8 32 28 – 36 3 33 17 51 30 – 40 1 39 23 23 Total norte = 40 Suma = -145 Ahora podemos observar que
norte = 40
Suma = -145
= 16 + (-145/40)
= 16 – 3.625
= 12,38
Por lo tanto, el número medio de días es 12,38 días en los que el estudiante estuvo ausente.
Pregunta 25. La siguiente tabla da la tasa de alfabetización (en porcentaje) de 35 ciudades. Hallar la tasa media de alfabetización.
| Tasa de alfabetización (en %): | 45 – 55 | 55 – 65 | 65 – 75 | 75 – 85 | 85 – 95 |
| Número de ciudades: | 3 | 10 | 11 | 8 | 3 |
Solución:
Podemos encontrar marcas de clase usando la relación
x = límite superior + límite de clase inferior2x =
Tamaño de la clase (h) para estos datos = 10
Ahora tomando 70 como media supuesta (a) incorrecta
Calcular d i , u i , f i u i de la siguiente manera
Tasa de alfabetización (en %) Número de ciudades (f i ) Valor medio x i re yo = x yo – 70 tu yo = re yo – 50 si yo tu yo 45 – 55 3 50 -20 -20 -6 55 – 65 10 60 -10 -1 -10 65 – 75 11 70 0 0 0 75 – 85 8 80 10 1 8 85 – 95 3 90 20 2 6 Total norte = 35 Suma = -2 Ahora podemos observar que
norte = 35
Suma = -2
= 70 + (-2/35)
= 70 – 4/7
= 70 – 0,57
= 69,43
Entonces, la tasa media de alfabetización es 69.43%
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA