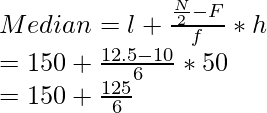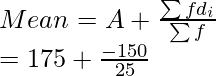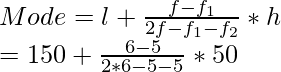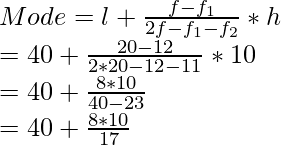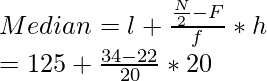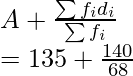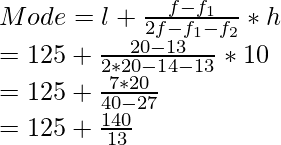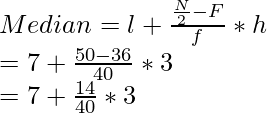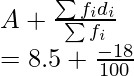Pregunta 11. Encuentra la media, la mediana y la moda de los siguientes datos:
| Clases | 0-50 | 50-100 | 100-150 | 150-200 | 200-250 | 250-300 | 300-350 |
| Frecuencia | 2 | 3 | 5 | 6 | 5 | 3 | 1 |
Solución:
Sea media (A) = 175
Clases marcas de clase
(X)
Frecuencia
(F)
cf re yo = x – A
A = 175
f i * d i 0-50 25 2 2 -150 -300 50-100 75 3 5 -100 -300 100-150 125 5 10 -50 -250 150-200 175-A 6 dieciséis 0 0 200-250 225 5 21 50 250 250-300 275 3 24 100 300 300-350 325 1 25 150 150 Total 25 -150 Encuentra la mediana:
Aquí N = 25, 5/3 = 25/2 = 12,5 o 13, se encuentra en el intervalo de clase = 50-200.
l = 150, F = 10, f = 6, h = 50
Usando la fórmula de la mediana, obtenemos
= 150 + 20,83
= 170,83
Encuentra la media:
Usando la fórmula media obtenemos
= 175 – 6
= 169
Modo de búsqueda:
Usando la fórmula de la moda obtenemos
= 150 + 25
= 175
Pregunta 12. Un estudiante anotó el número de automóviles que pasaban por un punto en una carretera durante 100 períodos de 3 minutos cada uno y lo resumió en la tabla que se muestra a continuación. Encuentre la moda de los datos.
| Número de coches | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Frecuencia | 7 | 14 | 13 | 12 | 20 | 11 | 15 | 8 |
Solución:
De la tabla dada concluimos que
Clase modal = 40-50 (tiene máxima frecuencia)
También,
l = 40, f = 20, f 1 = 12, f 2 = 11 y h = 10
Al usar la fórmula de la moda, obtenemos
= 40 + 4,70
= 44,7
Pregunta 13. La siguiente distribución de frecuencias da el consumo mensual de electricidad de 68 consumidores de una localidad. Encuentra la mediana, la media y la moda de los datos y compáralos:
| Consumo mensual (en unidades) | 65-85 | 85-105 | 105-125 | 125-145 | 145-165 | 165-185 | 185-205 |
| Nº de consumidores | 4 | 5 | 13 | 20 | 14 | 8 | 4 |
Solución:
Sea media (A) = 135
Consumo mensual Marcas de clase (x) Nº de consumidores (f) cf d = x – A f.d. 65-85 75 4 4 -60 -240 85-105 95 5 9 -40 -200 105-125 115 13 22 -20 -260 125-145 135 20 42 0 0 145-165 155 14 56 20 280 165-185 175 8 64 40 320 185-205 195 4 68 60 240 Total 68 140 Encuentra la mediana:
Aquí, N = 34
N/2 = 34,
Intervalo de clase = 25-145
También,
l = 125, F = 22, f = 20 y h = 20
Usando la fórmula de la mediana, obtenemos
= 125 + 12
= 137 unidades
Encuentra la media:
Usando la fórmula de la media, obtenemos
Media =
= 135 + 2,05
= 137,05 unidades
Modo de búsqueda:
Usando la fórmula de la moda, obtenemos
= 125 + 10,76
= 135,76 unidades
Pregunta 14. Se tomaron aleatoriamente 100 apellidos de un directorio telefónico local y se obtuvo la distribución de frecuencias del número de letras del alfabeto inglés en los apellidos de la siguiente manera:
| Número de letras | 1-4 | 4-7 | 7-10 | 10-13 | 13-16 | 16-19 |
| Número de apellidos | 6 | 30 | 40 | dieciséis | 4 | 4 |
Determine la mediana del número de letras en los apellidos. Encuentre el número medio de letras en los apellidos. También, Y el tamaño modal de los apellidos.
Solución:
Sea media (A) = 8.5
Número de letras Marcas de clase (x) Nº de apellidos (f) cf d = x-A f.d. 1-4 2.5 6 6 -6 -36 4-7 5.5 30 36 -3 -90 7-10 8.5-A 40 76 0 0 10-13 11.5 dieciséis 92 3 48 13-16 14.5 4 96 6 24 16-19 17.5 4 100 9 36 Total 100 -18 Encuentra la mediana:
Aquí, N = 100
Entonces, N/2 = 50
Intervalo de clase = 7-10
l = 7, F = 36, f = 40 y h = 3
Usando la fórmula de la mediana, obtenemos
= 7 + 1,05
= 8,05
Encuentra la media:
Usando la fórmula de la media, obtenemos
Media =
= 8,5 + 0,18
= 8,32
Modo de búsqueda:
Tenemos,
norte = 100
N/2 = 100/2 = 50
Aquí, la frecuencia acumulada es apenas mayor que N/2 = 76,
Por lo tanto, la clase mediana = 7 – 10
l = 7, h = 10 – 7 = 3, f = 40, F = 36
Usando la fórmula de la moda, obtenemos
Moda = l +
= 7 +
= 7 + 30/34
= 7 + 0,88
= 7,88
Pregunta 15. Encuentra la media, la mediana y la moda de los siguientes datos:
| Clase | 0 – 20 | 20 – 40 | 40 – 60 | 60 – 80 | 80 – 100 | 100 – 120 | 120 – 140 |
| Frecuencia | 6 | 8 | 10 | 12 | 6 | 5 | 3 |
Solución:
Intervalo de clases valor medio Frecuencia (f) efectos especiales Frecuencia acumulada 0 – 20 10 6 60 6 20 – 40 30 8 240 17 40 – 60 50 10 500 24 60 – 80 70 12 840 36 80 – 100 90 6 540 42 100 – 120 110 5 550 47 120 – 140 130 3 390 50 norte = 50 ∑fx = 3120 Encuentra la media:
Usando la fórmula de la media, obtenemos
Media =
Encuentra la mediana:
Tenemos,
norte = 50
Entonces, N/2 = 50/2 = 25
Aquí, la frecuencia acumulada apenas mayor que N/2 = 36
Por lo tanto, la clase mediana = 60 – 80
l = 60, h = 80 – 60 = 20, f = 12, F = 24
Usando la fórmula de la mediana, obtenemos
mediana = l +
= 60 +
= 60 + 20/12
= 60 + 1,67
= 61,67
Modo de búsqueda:
Tenemos,
La frecuencia máxima = 12
Clase de modelo = 60 – 80
l = 60, h = 80 – 60 = 20, f = 12, f 1 = 10, f 2 = 6
Usando la fórmula de la moda, obtenemos
Moda = l +
= 60 +
= 60 + 40/8
= 65
Pregunta 16. Los siguientes datos dan la distribución del gasto familiar mensual total de 200 familias de un pueblo. Encuentre el gasto modal mensual de las familias. Además, encuentre el gasto mensual medio:
| Gasto | Frecuencia | Gasto | Frecuencia |
| 1000 – 1500 | 24 | 3000 – 3500 | 30 |
| 1500 – 2000 | 40 | 3500 – 4000 | 22 |
| 2000 – 2500 | 33 | 4000 – 4500 | dieciséis |
| 2500 – 3000 | 28 | 4500 – 5000 | 7 |
Solución:
De la tabla dada concluimos que
La frecuencia máxima de clase = 40
Entonces, clase modal = 1500 – 2000
l = 1500, f = 40, h = 500, f 1 = 24, f 2 = 33
Usando la fórmula de la moda, obtenemos
Moda = l +
= 1500 +
= 1500 +
= 1500 + 347.826
= 1847,826 ≈ 1847,83
Por lo tanto, el gasto mensual modal = Rs. 1847.83
Ahora encontraremos marcas de clase como
nota de clase =
Tamaño de clase (h) de datos dados = 500
Sea mean(a) = 2750, ahora vamos a calcular d i u i de la siguiente manera:
Gastos (en Rs) Número de familias f i X yo d yo = x yo – 2750 tu yo si yo tu yo 1000 – 1500 24 1250 -1500 -3 -72 1500 – 2000 40 1750 -1000 -2 -80 2000 – 2500 33 2250 -500 -1 -33 2500 – 3000 28 2750 0 0 0 3000 – 3500 30 3250 500 1 30 3500 – 4000 22 3750 1000 2 44 4000 – 4500 dieciséis 4250 1500 3 48 4500 – 5000 7 4750 2000 4 28 Total 200 -35 De la tabla concluimos que
∑f i = 200
∑f yo re yo = -35
Media
= a +
= 2750 +
= 2750 – 87,5
= 2662.5
Por lo tanto, el gasto mensual medio = Rs. 2662.5
Pregunta 17. La distribución dada muestra el número de carreras anotadas por algunos de los mejores bateadores del mundo en partidos internacionales de cricket de un día.
| carreras anotadas | No. de bateadores | carreras anotadas | No. de bateadores |
| 3000 – 4000 | 4 | 7000 – 8000 | 6 |
| 4000 – 5000 | 18 | 8000 – 9000 | 3 |
| 5000 – 6000 | 9 | 9000 – 10000 | 1 |
| 6000 – 7000 | 7 | 10000 – 11000 | 1 |
Encuentre la moda de los datos
Solución:
De la tabla dada concluimos que
La frecuencia de clase máxima = 18
Entonces, clase modal = 4000 – 5000
y
l = 4000, f = 18, h = 1000, f 1 = 4, f 2 = 9
Usando la fórmula de la moda, obtenemos
Moda = l +
= 4000 +
= 4000 + (14000/23)
= 4000 + 608.695
= 4608.695
Por lo tanto, la moda de los datos dados = 4608.7 carreras.
Pregunta 18. A continuación se presenta la tabla de distribución de frecuencias de las explotaciones agrícolas en un pueblo:
| Superficie de terreno (en hectáreas): | 1 – 3 | 3 – 5 | 5 – 7 | 7 – 9 | 9 – 11 | 11 – 13 |
| Número de familias | 20 | 45 | 80 | 55 | 40 | 12 |
Encuentre las explotaciones agrícolas modales del pueblo.
Solución:
De la tabla dada concluimos que
La frecuencia de clase máxima = 80,
Entonces, la clase modal = 5-7
y
l = 5, f 0 = 45, h = 2, f 1 = 80, f 2 = 55
Usando la fórmula de la moda, obtenemos
Moda = l +
= 5 +
= 5 +
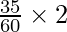
= 5 +
= 5 + 1,2
= 6,2
Entonces, las explotaciones agrícolas modales del pueblo = 6,2 hectáreas.
Pregunta 19. Los ingresos mensuales de 100 familias se dan a continuación:
| Ingresos en (en Rs) | Número de familias |
| 0 – 5000 | 8 |
| 5000 – 10000 | 26 |
| 10000 – 15000 | 41 |
| 15000 – 20000 | dieciséis |
| 20000 – 25000 | 3 |
| 25000 – 30000 | 3 |
| 30000 – 35000 | 2 |
| 35000 – 40000 | 1 |
Calcular el ingreso modal.
Solución:
De la tabla dada concluimos que
La frecuencia de clase máxima = 41,
Entonces, clase modal = 10000-15000.
Aquí, l = 10000, f 1 = 41, f 0 = 26, f 2 = 16 y h = 5000
Por lo tanto, usando la fórmula de la moda, obtenemos
Moda = l +
= 10000 +
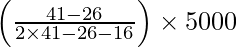
= 10000 +
= 10000 +
= 10000 + 15 × 125
= 10000 + 1875
= 11875
Entonces, el ingreso modal = Rs. 11875.