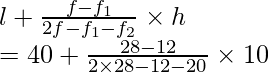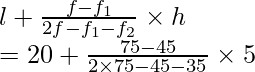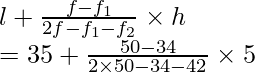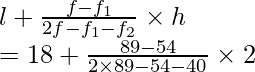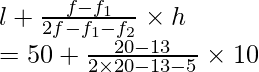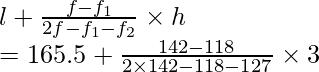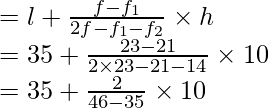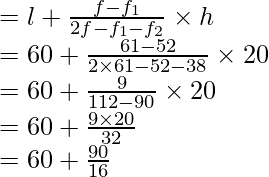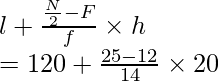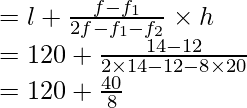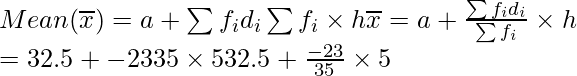Clase 10 Soluciones RD Sharma – Capítulo 7 Estadísticas – Ejercicio 7.5

Pregunta 1. Encuentra la moda de los siguientes datos:

(i) 3, 5, 7, 4, 5, 3, 5, 6, 8, 9, 5, 3, 5, 3, 6, 9, 7, 4

(ii) 3, 3, 7, 4, 5, 3, 5, 6, 8, 9, 5, 3, 5, 3, 6, 9, 7, 4

(iii) 15, 8, 26, 25, 24, 15, 18, 20, 24, 15, 19, 15

Solución:

(i)

Valor (x) 3 4 5 6 7 8 9

Frecuencia (f) 4 2 5 2 2 1 2

Por lo tanto, moda = 5 porque 5 ocurre el número máximo de veces.

(ii)

Valor (x) 3 4 5 6 7 8 9

Frecuencia (f) 5 2 4 2 2 1 2

Por lo tanto, moda = 3 porque 3 ocurre el número máximo de veces.

(iii)

Valor (x) 8 15 18 19 20 24 25

Frecuencia (f) 1 4 1 1 1 2 1

Por lo tanto, moda = 15 porque 15 ocurre el número máximo de veces.

Pregunta 2. Las tallas de camisa usadas por un grupo de 200 personas, que compraron la camisa en una tienda, son las siguientes:

Talla de camisa:	37	38	39	40	41	42	43	44
Número de personas:	15	25	39	41	36	17	15	12

Encuentra el modelo de talla de camiseta que usa el grupo.

Solución:

De los datos presentados en la tabla concluimos que

Talla de camiseta del modelo = 40

Porque la talla de camiseta 40 ocurrió la mayor cantidad de veces.

Pregunta 3. Encuentra la moda de la siguiente distribución.

(i)

Intervalo de clases:	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60	60 – 70	70 – 80
Frecuencia:	5	8	7	12	28	20	10	10

Solución:

De la tabla dada concluimos que

La frecuencia máxima = 28

Entonces, la clase del modelo = 40 – 50

y,

l = 40, h = 50 40 = 10, f = 28, f1 = 12, f2 = 20

Usando la fórmula de la moda

Modo = $l+\frac{f-f_1}{2f-f_1-f_2}\times h\\ =40+\frac{28-12}{2\times28-12-20}\times10$

= 40 + 160/ 24

= 40 + 6,67

= 46,67

Por lo tanto, la moda = 46.67

(ii)

Intervalo de clases	10 – 15	15 – 20	20 – 25	25 – 30	30 – 35	35 – 40
Frecuencia	30	45	75	35	25	15

Solución:

De la tabla dada concluimos que

La frecuencia máxima = 75

Entonces, la clase modal = 20 – 25

Y,

l = 20, h = 25 – 20 = 5, f = 75, f ₁ = 45, f ₂ = 35

Usando la fórmula de la moda

Modo = $l+\frac{f-f_1}{2f-f_1-f_2}\times h\\ =20+\frac{75-45}{2\times75-45-35}\times5$

= 20 + 150/70

= 20 + 2,14

= 22,14

Por lo tanto, la moda = 22.14

(iii)

Intervalo de clases	25 – 30	30 – 35	35 – 40	40 – 45	45 – 50	50 – 55
Frecuencia	25	34	50	42	38	14

Solución:

De la tabla dada concluimos que

La frecuencia máxima = 50

Entonces, la clase modal = 35 – 40

Y,

l = 35, h = 40 – 35 = 5, f = 50, f ₁ = 34, f ₂ = 42

Usando la fórmula de la moda

Modo = $l+\frac{f-f_1}{2f-f_1-f_2}\times h\\ =35+\frac{50-34}{2\times50-34-42}\times5$

= 35 + 80/24

= 35 + 3,33

= 38,33

Por lo tanto, la moda = 38.33

Pregunta 4. Compare las edades modales de dos grupos de estudiantes que se presentan a una prueba de ingreso:

Edad en años	16 – 18	18 – 20	20 – 22	22 – 24	24 – 26
Grupo A	50	78	46	28	23
Grupo B	54	89	40	25	17

Solución:

Para el Grupo A:

De la tabla dada concluimos que

La frecuencia máxima = 78.

Entonces, la clase modelo = 18 – 20

Y,

l = 18, h = 20 – 18 = 2, f = 78, f ₁ = 50, f ₂ = 46

Usando la fórmula de la moda

Modo = $l+\frac{f-f_1}{2f-f_1-f_2}\times h\\ =18+\frac{78-50}{2\times78-50-46}\times2$

= 18 + 56/60

= 18 + 0,93

= 18,93 años

Para el Grupo B:

De la tabla dada concluimos que

La frecuencia máxima = 89

La clase modal = 18 – 20

Y,

l = 18, h = 20 – 18 = 2, f = 89, f ₁ = 54, f ₂ = 40

Usando la fórmula de la moda

Modo = $l+\frac{f-f_1}{2f-f_1-f_2}\times h\\ =18+\frac{89-54}{2\times89-54-40}\times2$

= 18 + 70/84

= 18 + 0,83

= 18,83 años

Después de encontrar la moda de los grupos A y B, concluimos que

la edad modal del Grupo A es mayor que la del Grupo B.

Pregunta 5. Las calificaciones en ciencias de 80 estudiantes de la clase X se dan a continuación. Encuentre la moda de las calificaciones obtenidas por los estudiantes en ciencias.

Marcas	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60	60 – 70	70 – 80	80 – 90	90 – 100
Frecuencia	3	5	dieciséis	12	13	20	5	4	1	1

Solución:

De la tabla dada concluimos que

La frecuencia máxima = 20

La clase modal = 50 – 60

Y,

l = 50, h = 60 – 50 = 10, f = 20, f ₁ = 13, f ₂ = 5

Usando la fórmula de la moda

Modo = $l+\frac{f-f_1}{2f-f_1-f_2}\times h\\ =50+\frac{20-13}{2\times20-13-5}\times10$

= 50 + 70/22

= 50 + 3,18

= 53,18

Por lo tanto, la moda = 53.18

Pregunta 6. La siguiente es la distribución de altura de los estudiantes de cierta clase en una ciudad:

Altura (en cm)	160 – 162	163 – 165	166 – 168	169 – 171	172 – 174
Nº de alumnos:	15	118	142	127	18

Encuentre la altura promedio del número máximo de estudiantes.

Solución:

Alturas (exclusivo)	160 – 162	163 – 165	166 – 168	169 – 171	172 – 174
Alturas (incluidas)	159,5 – 162,5	162,5 – 165,5	165,5 – 168,5	168,5 – 171,5	171,5 – 174,5
No de estudiantes	15	118	142	127	18

De la tabla dada concluimos que

La frecuencia máxima = 142

La clase modal = 165.5 – 168.5

Y,

l = 165,5, h = 168,5 – 165,5 = 3, f = 142, f ₁ = 118, f ₂ = 127

Usando la fórmula de la moda

Modo = $l+\frac{f-f_1}{2f-f_1-f_2}\times h\\ =165.5+\frac{142-118}{2\times142-118-127}\times3$

= 165,5 + 72/39

= 165,5 + 1,85

= 167,35cm

Por lo tanto, la altura promedio del número máximo de estudiantes = 167,35 cm

Pregunta 7. La siguiente tabla muestra las edades de los pacientes ingresados en un hospital durante un año:

Edades (en años):	5 – 15	15 – 25	25 – 35	35 – 45	45 – 55	55 – 65
No de estudiantes:	6	11	21	23	14	5

Encuentre la moda y la media de los datos anteriores. Compare e interprete las dos medidas de tendencia central.

Solución:

Por media:

Consideremos la media (A) = 30

Edad en años) Número de pacientes _fi Marcas de clase x _i re _yo = x _yo – 275 si _yo si _yo

5 – 15 6 10 -20 -120

15 – 25 11 20 -10 -110

25 – 35 21 30 0 0

35 – 45 23 40 10 230

45 – 55 14 50 20 280

55 – 65 5 60 30 150

norte = 80 $\sum f_id_i=430$

De la tabla obtenemos

Σf _yo = N = 80 y Σf yo re _yo₌ 430.

Usando la fórmula de la media

$Mean\ (\overline{x})=A+\frac{\sum f_id_i}{\sum f_i}$

= 30 + 430/80

= 30 + 5.375

= 35.375

= 35,38

Por lo tanto, la media = 35,38. Representa la edad promedio de los pacientes = 35,38 años.

Para el modo:

De la tabla dada concluimos que

La frecuencia de clase máxima = 23

Entonces, clase modal = 35 – 45

y

l = 35, f = 23, h = 10, f ₁ = 21, f ₂ = 14

Usando la fórmula de la moda

Modo $=l+\frac{f-f_1}{2f-f_1-f_2}\times h\\ =35+\frac{23-21}{2\times23-21-14}\times10\\ =35+\frac{2}{46-35}\times10$

= 35 + 1,81 = 36,8

Por lo tanto, la moda = 36,8. Representa el número máximo de pacientes ingresados en el hospital de 36,8 años de edad.

Por lo tanto, la moda es mayor que la media.

Pregunta 8. Los siguientes datos brindan información sobre la vida útil observada (en horas) de 225 componentes eléctricos:

Tiempos de vida (en horas):	0 – 20	20 – 40	40 – 60	60 – 80	80 – 100	100 – 120
Nº de componentes:	10	35	52	61	38	29

Determine las vidas modales de los componentes.

Solución:

De la tabla dada concluimos que

La frecuencia máxima de clase = 61

Entonces, clase modal = 60 – 80

y

l = 60, f = 61, h = 20, f ₁ = 52, f ₂ = 38

Usando la fórmula de la moda

Modo $=l+\frac{f-f_1}{2f-f_1-f_2}\times h\\ =60+\frac{61-52}{2\times61-52-38}\times20\\ =60+\frac{9}{112-90}\times20\\ =60+\frac{9\times20}{32}\\ =60+\frac{90}{16}$

= 60 + 5,625 = 65,625

Por lo tanto, la vida útil modal de los componentes eléctricos = 65,625 horas

Pregunta 9. La siguiente tabla da el ingreso diario de 50 trabajadores de una fábrica:

Ingreso diario	100 – 120	120 – 140	140 – 160	160 – 180	180 – 200
Numero de trabajadores	12	14	8	6	10

Encuentre la media, la moda y la mediana de los datos anteriores.

Solución:

Encontrar la media:

De la tabla obtenemos

N = 50, fx = 7260

Entonces, usando la fórmula media, obtenemos

Media = Σfx / N

= 7260/ 50

= 145,2

Por lo tanto, la media = 145,2

Encontrar la mediana:

N/2 = 50/2 = 25

Entonces, la frecuencia acumulada es mayor que N/2 = 26,

La clase mediana = 120 – 140

Tal que l = 120, h = 140 – 120 = 20, f = 14, F = 12

Usando la fórmula de la mediana obtenemos

mediana = $l+\frac{\frac{N}{2}-F}{f}\times h\\ =120+\frac{25-12}{14}\times20$

= 120 + 260/14

= 120 + 18,57

= 138,57

Por lo tanto, la mediana = 138.57

Modo de búsqueda:

De la tabla obtenemos

La frecuencia máxima = 14,

Entonces la clase modal = 120 – 140

Y,

l = 120, h = 140 – 120 = 20, f = 14, f ₁ = 12, f ₂ = 8

Usando la fórmula de la moda obtenemos

Modo = $=l+\frac{f-f_1}{2f-f_1-f_2}\times h\\ =120+\frac{14-12}{2\times14-12-8\times20}\\ =120+\frac{40}{8}$

= 120 + 5

= 125

Por lo tanto, la moda = 125

Pregunta 10. La siguiente distribución da la relación maestros-alumnos por estado en las escuelas secundarias superiores de la India. Encuentra la moda y la media de estos datos. Interpreta las dos medidas:

Número de alumnos por profesor	Número de estados/UT
15 – 20	3
20 – 25	8
25 – 30	9
30 – 35	10
35 – 40	3
40 – 45	0
45 – 50	0
50 – 55	2

Solución:

De la tabla dada concluimos que

La frecuencia de clase máxima = 10

Entonces, clase modal = 30 – 35

y

l = 30, h = 5, f = 10, f ₁ = 9, f ₂ = 3

Usando la fórmula de la moda obtenemos

Moda = l + f – f ₁ 2f – f ₁ – f ₂ × hl + $=\frac{f-f_1}{2f-f_1-f_2}\times h\\$

= 30 + 120 – 12 × 530 + $\frac{10-9}{2\times10-9-3}\times5$

= 30 + 120 – 12 × 530 + $\frac{1}{20-12}\times5$

= 30 + 5/8

= 30.625

Por lo tanto, la moda = 30.6 y representa que la mayoría de los estados/UT tienen una relación docente-alumnos = 30.6

Ahora vamos a encontrar las marcas de clase usando la siguiente fórmula

nota de clase = $\frac{upperclasslimit+lowerclasslimit}{2}$

Consideremos la media (a) = 32.5, y ahora vamos a encontrar d _i , u _i y f _i u _i de la siguiente manera

Número de alumnos por profesor Número de estados/ UT (f _i ) x _yo re _yo = x _yo – 32.5 tu _yo si _yo tu _yo

15 – 20 3 17.5 -15 -3 -9

20 – 25 8 22.5 -10 -2 -dieciséis

25 – 30 9 27.5 -5 -1 -9

30 – 35 10 32.5 0 0 0

35 – 40 3 37.5 5 1 3

40 – 45 0 42.5 10 2 0

45 – 50 0 47.5 10 2 0

50 – 55 2 52.5 20 4 8

Total 35 -23

Usando la fórmula de la media, obtenemos

$Mean(\overline{x})=a+\sum f_id_i\sum f_i\times h\overline{x}=a+\frac{\sum f_id_i}{\sum f_i}\times h\\ =32.5+-2335\times532.5+\frac{-23}{35}\times5$

= 32,5 – 23/7

= 32,5 – 3,28

= 29,2

Por lo tanto, la media = 29,2 y representa que, en promedio, la relación maestro-alumno = 29,2.

Publicación traducida automáticamente

Artículo escrito por yippeee25 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 10 Soluciones RD Sharma – Capítulo 7 Estadísticas – Ejercicio 7.5 | Serie 1

Pregunta 1. Encuentra la moda de los siguientes datos:

(i) 3, 5, 7, 4, 5, 3, 5, 6, 8, 9, 5, 3, 5, 3, 6, 9, 7, 4

(ii) 3, 3, 7, 4, 5, 3, 5, 6, 8, 9, 5, 3, 5, 3, 6, 9, 7, 4

(iii) 15, 8, 26, 25, 24, 15, 18, 20, 24, 15, 19, 15

Pregunta 2. Las tallas de camisa usadas por un grupo de 200 personas, que compraron la camisa en una tienda, son las siguientes:

Encuentra el modelo de talla de camiseta que usa el grupo.

Pregunta 3. Encuentra la moda de la siguiente distribución.

(i)

(ii)

(iii)

Pregunta 4. Compare las edades modales de dos grupos de estudiantes que se presentan a una prueba de ingreso:

Pregunta 5. Las calificaciones en ciencias de 80 estudiantes de la clase X se dan a continuación. Encuentre la moda de las calificaciones obtenidas por los estudiantes en ciencias.

Pregunta 6. La siguiente es la distribución de altura de los estudiantes de cierta clase en una ciudad:

Encuentre la altura promedio del número máximo de estudiantes.

Pregunta 7. La siguiente tabla muestra las edades de los pacientes ingresados en un hospital durante un año:

Encuentre la moda y la media de los datos anteriores. Compare e interprete las dos medidas de tendencia central.

Pregunta 8. Los siguientes datos brindan información sobre la vida útil observada (en horas) de 225 componentes eléctricos:

Determine las vidas modales de los componentes.

Pregunta 9. La siguiente tabla da el ingreso diario de 50 trabajadores de una fábrica:

Encuentre la media, la moda y la mediana de los datos anteriores.

Pregunta 10. La siguiente distribución da la relación maestros-alumnos por estado en las escuelas secundarias superiores de la India. Encuentra la moda y la media de estos datos. Interpreta las dos medidas:

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra la moda de los siguientes datos:

(i) 3, 5, 7, 4, 5, 3, 5, 6, 8, 9, 5, 3, 5, 3, 6, 9, 7, 4

(ii) 3, 3, 7, 4, 5, 3, 5, 6, 8, 9, 5, 3, 5, 3, 6, 9, 7, 4

(iii) 15, 8, 26, 25, 24, 15, 18, 20, 24, 15, 19, 15

Pregunta 2. Las tallas de camisa usadas por un grupo de 200 personas, que compraron la camisa en una tienda, son las siguientes:

Encuentra el modelo de talla de camiseta que usa el grupo.

Pregunta 3. Encuentra la moda de la siguiente distribución.

(i)

(ii)

(iii)

Pregunta 4. Compare las edades modales de dos grupos de estudiantes que se presentan a una prueba de ingreso:

Pregunta 5. Las calificaciones en ciencias de 80 estudiantes de la clase X se dan a continuación. Encuentre la moda de las calificaciones obtenidas por los estudiantes en ciencias.

Pregunta 6. La siguiente es la distribución de altura de los estudiantes de cierta clase en una ciudad:

Encuentre la altura promedio del número máximo de estudiantes.

Pregunta 7. La siguiente tabla muestra las edades de los pacientes ingresados ​​en un hospital durante un año:

Encuentre la moda y la media de los datos anteriores. Compare e interprete las dos medidas de tendencia central.

Pregunta 8. Los siguientes datos brindan información sobre la vida útil observada (en horas) de 225 componentes eléctricos:

Determine las vidas modales de los componentes.

Pregunta 9. La siguiente tabla da el ingreso diario de 50 trabajadores de una fábrica:

Encuentre la media, la moda y la mediana de los datos anteriores.

Pregunta 10. La siguiente distribución da la relación maestros-alumnos por estado en las escuelas secundarias superiores de la India. Encuentra la moda y la media de estos datos. Interpreta las dos medidas:

Deja una respuesta Cancelar la respuesta

Pregunta 7. La siguiente tabla muestra las edades de los pacientes ingresados en un hospital durante un año: