Clase 10 Soluciones RD Sharma – Capítulo 9 Progresiones aritméticas – Ejercicio 9.6 | conjunto 2

Pregunta 25. En un AP el primer término es 22, el n-ésimo término es –11 y la suma del primer n término es 66. Encuentra n y la d, la diferencia común.  

Solución:

Dado que AP tiene el primer término (a) = 22, el enésimo término (a _n ) = –11 y la suma (S _n ) = 123.

Ahora usando la fórmula de la suma de n términos de un AP

S _norte = norte[un + un _norte ] / 2

=> 66 = n[22 + (−11)]/2

=> 66 = n[22 − 11]/2

=> 11n = 132

=> norte = 12

Usando la fórmula del enésimo término de un AP

un norte = un + ( _n – 1)d

=> −11 = 22 + (12 – 1)d

=> 11d = –33

=> d = –3 

Por lo tanto, el número de términos de AP dado es 12 y la diferencia común es -3.

Pregunta 26. El primer y último término de un AP son 7 y 49 respectivamente. Si la suma de todos sus términos es 420, encuentra la diferencia común.

Solución:

Dado que AP tiene el primer término (a) = 7, el último término (a _n ) = 49 y la suma (S _n ) = 420.

Ahora usando la fórmula de la suma de n términos de un AP

S _norte = norte[un + un _norte ] / 2

Asi que, 

=> 420 = n[7 + 49]/2

=> 28n = 420

=> n = 15

Usando la fórmula del enésimo término de un AP

un norte = un + ( _n – 1)d

Asi que, 

=> 49 = 7 + (15 – 1)d

=> 14 días = 42

=> re = 3

Por lo tanto, la diferencia común del AP dado es 3.

Pregunta 27. El primer y último término de un AP son 5 y 45 respectivamente. Si la suma de todos sus términos es 400, encuentra su diferencia común.

Solución:

Dado que AP tiene el primer término (a) = 5, el último término (a _n ) = 45 y la suma (S _n ) = 400.

Ahora usando la fórmula de la suma de n términos de un AP

S _norte = norte[un + un _norte ] / 2

=> 400 = n[5 + 45]/2

=> 25n = 400

=> n = 16

Usando la fórmula del enésimo término de un AP

un norte = un + ( _n – 1)d

Asi que, 

=> 45 = 5 + (16 – 1)d

=> 15d = 40

=> re = 8/3

Por lo tanto, la diferencia común del AP dado es 8/3.

Pregunta 28. La suma de los primeros 9 términos de un AP es 162. La razón de su 6.° término a su 13.° término es 1:2. Encuentra el primer y el 15.° término del AP

Solución:

Sabemos que la suma de n términos de un AP viene dada por S _n = n[2a + (n − 1)d] / 2.

Por lo tanto, Suma de los primeros 9 términos de AP dado = S ₉ = 9[2a + (9 − 1)d] / 2 = 162

=> 162 = 9(2a + (9 − 1)d) / 2

=> 2a + 8d = 36

=> a + 4d = 18 …..(1)

Usando la fórmula del enésimo término de un AP

un norte = un + ( _n – 1)d

Asi que, 

Dado un ₆ : un ₁₃ = 1 : 2,

=> un ₁₃ = 2a ₆ 

=> a+12d = 2(a + 5d)

=> a+12d = 2a + 10d

=> a = 2d …..(2)

Al poner (2) en (1), obtenemos,

=> 2d + 4d = 18

=> 6d = 18

=> re = 3

Al poner d = 3 en (2), obtenemos,

a = 2(3) = 6, que es el primer término.

Ahora el término 15, a ₁₅ = a + 14d = 6 + 14 × 3 = 6 + 42 = 48

Por lo tanto, el primer y decimoquinto término del AP son 6 y 48 respectivamente.

Pregunta 29. Si el décimo término de un AP es 21 y la suma de sus primeros 10 términos es 120, encuentra su enésimo término.

Solución:

Usando la fórmula del enésimo término de un AP

un norte = un + ( _n – 1)d

Asi que, 

Décimo término del AP dado, a ₁₀ = 21

=> a + 9d = 21 …..(1)

Usando la fórmula de la suma de n términos de un AP 

S _norte = norte[2a + (norte – 1)d] / 2.

Asi que,

S ₁₀ = 10[2a + (10 − 1)d] / 2

=> 120 = 5(2a + 9d)

=> 2a + 9d = 24 …. (2)

Al restar (1) de (2), obtenemos

=> 2a + 9d – a – 9d = 24 – 21

=> un = 3

Al poner a = 3 en la ecuación (1), obtenemos,

=> 3 + 9d = 21

=> 9d = 18

=> re = 2

Entonces, un _n = 3 + (n – 1)2

= 3 + 2n – 2

= 2n + 1

Por lo tanto, el término n del AP dado es 2n + 1.

Pregunta 30. La suma de los primeros 7 términos de un AP es 63 y la suma de sus siguientes 7 términos es 161. Encuentra el término 28 de este AP

Solución:

Suma de los primeros 7 términos de un AP, S ₇ = 63.

Y la suma de los siguientes 7 términos es 161. 

Entonces, la suma de los primeros 14 términos, S ₁₄ = Suma de los primeros 7 términos + Suma de los siguientes 7 términos

S ₁₄ = 63 + 161 = 224

Usando la fórmula de la suma de n términos de un AP 

S _norte = norte[2a + (norte – 1)d] / 2.

Entonces, S ₇ = 7(2a + (7 − 1)d) / 2

=> 7(2a + 6d) / 2 = 63

=> 2a + 6d = 18 . . . . (1)

Además, S ₁₄ = 14(2a + (14 − 1)d) / 2

=> 14(2a+13d)/2 = 224

=> 2a+13d = 32 . . . . (2)

Ahora, restando la ecuación (1) de la ecuación (2), obtenemos

=> 13d – 6d = 32 – 18

=> 7d = 14

=> re = 2

Al poner d = 2 en la ecuación (1), obtenemos,

=> 2a + 6(2) = 18

=> 2a = 18 – 12

=> un = 3

Así, a ₂₈ = a + (28 – 1)d = 3 + 27 (2) = 3 + 54 = 57

Por lo tanto, el término 28 es 57.

Pregunta 31. La suma de los primeros siete términos de un AP es 182. Si sus términos 4 y 17 están en proporción 1: 5, encuentre el AP

Solución:

Usando la fórmula de la suma de n términos de un AP 

S _norte = norte[2a + (norte – 1)d] / 2.

Entonces, S ₇ = 7(2a + (7 − 1)d) / 2

=> 7(2a + 6d) = 364

=> 14a + 42d = 364

=> a + 3d = 26 .… (1)

Usando la fórmula del enésimo término de un AP

un norte = un + ( _n – 1)d

Asi que, 

Nos dan, a ₄ : a ₁₇ = 1:5

=> un ₁₇ = 5a ₄

=> a+16d = 5[a + 3d]

=> a + 16d = 5a + 15d

=> 4a = re…. (2)

Usando eq(2) en eq(1), obtenemos,

=> un + 3(4a) = 26 

=> 13a = 26

=> un = 2

Al poner a = 2 en la ecuación (2), obtenemos,

=> re = 8

Como el primer término del AP dado es 2 y 

la diferencia común es 8, entonces, el AP es 2, 10, 18, 26, …..

Pregunta 32. El n-ésimo término de un AP está dado por (−4n + 15). Encuentre la suma de los primeros 20 términos de este AP

Solución:

Nos dan el enésimo término del AP, a _n = −4n + 15.

Al poner n = 1 para encontrar el primer término de nuestro PA, a = −4(1) + 15 = 11

Al poner n = 20 para encontrar el vigésimo término del AP, a20 = −4(20) + 15 = −65

Usando la fórmula de la suma de los primeros n términos de un AP 

S _norte = norte [un + un _norte ] / 2.

Entonces, S ₂₀ = 20 [11 + (−65)] / 2

= 10(−54) = −540

Por lo tanto, la suma de los primeros 20 términos de este AP es −540.

Pregunta 33. En un AP la suma de los primeros diez términos es −150 y la suma de sus próximos 10 términos es −550. Encuentre el punto de acceso

Solución:

Suma de los diez primeros términos, S ₁₀ = −150.

También dado, Suma de sus siguientes 10 términos = −550

Suma de los primeros 20 términos, S ₂₀ = Suma de los primeros 10 términos + Suma de los siguientes 10 términos

=> S ₂₀ = −150 + (−550) = −700

Usando la fórmula de la suma de n términos de un AP 

S _norte = norte[2a + (norte – 1)d] / 2.

Entonces, S ₁₀ = 10(2a + (10 − 1)d) / 2

=> −150 = 5(2a + 9d)

=> 2a + 9d = –30 ….. (1)

Y también, S ₂₀ = 20(2a + (20 − 1)d) / 2

=> −700 = 10(2a + 19d)

=> 2a + 19d = −70 ….. (2)

Ahora, restando la ecuación (1) de (2), obtenemos

=> 19d – 9d = –70 – (–30)

=> 10d = –40

=> d = –4

Al poner d = –4 en (1), obtenemos,

=> 2a + 9(–4) = –30

=> 2a = 6

=> un = 3

Como tenemos a = 3 y d = –4, entonces el AP es 3, –1, –5, –9,…..

Pregunta 34. La suma de los primeros 14 términos de un AP es 1505 y su primer término es 10. Encuentra su término 25.

Solución:

Dado que AP tiene el primer término (a) = 10 y la suma de los primeros 14 términos, S ₁₄ = 1505.

Usando la fórmula de la suma de n términos de un AP 

S _norte = norte[2a + (norte – 1)d] / 2.

=> S ₁₄ = 14(2(10) + (14 − 1)d) / 2 = 1505

=> 7(20 + 13d) = 1505

=> 20 + 13d = 215

=> 13d = 195

=> re =15

Sabemos que el término 25 es a ₂₅ = 10 + (25 − 1)15

= 10 + 24(15)

= 370

Por lo tanto, el término 25 del AP es 370.

Pregunta 35. En un AP, el primer término es 2, el último término es 29 y la suma de los términos es 155. Encuentra la diferencia común de los AP

Solución:

Dado que AP tiene el primer término (a) = 2, el último término (a _n ) = 29 y la suma (S _n ) = 155.

Usando la fórmula de la suma de los primeros n términos de un AP 

S _norte = norte [un + un _norte ] / 2.

=> 155 = n(2 + 29) / 2

=> 31n = 310

=> norte = 10

Usando la fórmula del enésimo término de un AP

un norte = un + ( _n – 1)d

Asi que, 

=> 29 = 2 + (10 – 1)d

=> 9d = 27

=> re = 3

Por lo tanto, la diferencia común de AP es 3.

Pregunta 36. El primer y último término de un AP son 17 y 350 respectivamente. Si la diferencia común es 9, ¿cuántos términos hay y cuál es su suma?

Solución:

Dado que AP tiene el primer término (a) = 17, la diferencia común (d) = 9 y el último término (a _n ) = 350.

Usando la fórmula del enésimo término de un AP

un norte = un + ( _n – 1)d

Asi que, 

=> 350 = 17 + (n – 1) 9

=> 350 = 17 + 9n – 9

=> 9n = 342

=> norte = 38

Usando la fórmula de la suma de los primeros n términos de un AP 

S _norte = norte [un + un _norte ] / 2.

S ₃₈ = 38(17 + 350)/2

= 19(367) = 6973

Por lo tanto, el número de términos del AP dado es 38 y la suma es 6973.

Pregunta 37. Halla el número de términos del AP –12, –9, –6, . . . , 21. Si se suma 1 a cada término de este AP, entonces encuentre la suma de todos los términos del AP así obtenido.

Solución:

Si se suma 1 a cada término del AP, entonces el nuevo AP es –11, –8, –5, . . . , 22.

Primer término, a = –11 y diferencia común, d = – 8 – (–11) = 3

Y sabemos que enésimo término = a _n = a + (n – 1)d

=> 22 = –11 + (n – 1)3

=> 3n = 36

=> norte = 12

Usando la fórmula de la suma de los primeros n términos de un AP 

S _norte = norte [un + un _norte ] / 2.

=> S ₁₂ = 12[–11 + 22]/2

= 6[11]

= 66

Por tanto, la suma después de sumar 1 a cada uno de los términos del AP es 66.

Pregunta 38. La suma de los primeros n términos de un AP es 3n ² + 6n. Encuentre el enésimo término de este AP

Solución:

Dado S _n = 3n ² + 6n

Al poner n = 1, obtenemos el primer término(a), S ₁ = a = 3(1) ² + 6(1) = 9 

Al poner n = 2 da S ₂ = a + a + d = 3(2) ² + 6(2) = 24

=> re = 24 – 2a

=> re = 24 – 18 = 6

Usando la fórmula del enésimo término de un AP

un norte = un + ( _n – 1)d

Asi que, 

= 9 + (n – 1)6

= 9 + 6n – 6

= 6n + 3

Por lo tanto, el término n del AP dado es 6n + 3.

Pregunta 39. La suma de los primeros n términos de un AP es 5n – n ² . Encuentre el enésimo término de este AP

Solución:

Dado S _n = 5n – n ² ,

Al poner n = 1, obtenemos el primer término(a), S ₁ = a = 5(1) – (1) ² = 4

Al poner n = 2 da S ₂ = a + a + d = 5(2) – (2) ² = 6

=> re = 6 – 2a

=> d = 6 – 8 = –2

Usando la fórmula del enésimo término de un AP

un norte = un + ( _n – 1)d

Asi que, 

= 4 + (n – 1)(–2)

= 4 – 2n + 2

= 6 – 2n

Por lo tanto, el término n del AP dado es 6 – 2n.

Pregunta 40. La suma de los primeros n términos de un AP es 4n ² + 2n. encuentra el n-ésimo término de este AP

Solución:

Dado S _n = 4n ² + 2n,

Al poner n = 1, obtenemos el primer término(a), S ₁ = a = 4(1) ² + 2(1) = 6 

Al poner n = 2 da S ₂ = a + a + d = 4(2) ² + 2(2) = 20

=> d = 20 – 2a

=> d = 20–12 = 8 

Usando la fórmula del enésimo término de un AP

un norte = un + ( _n – 1)d

Asi que, 

= 6 + (n – 1)8

= 6 + 8n – 8

= 8n – 2

Por lo tanto, el término n del AP dado es 8n – 2.

Pregunta 41. La suma de los primeros n términos de un AP es 3n ² + 4n. encontrar el término 25 de este AP

Solución:

Dado S _n = 3n ² + 4n,

Al poner n = 1, obtenemos el primer término(a), S ₁ = a = 3(1) ² + 4(1) = 7

Al poner n = 2 da S ₂ = a + a + d = 3(2) ² + 4(2) = 20

=> d = 20 – 2a

=> d = 20–14 = 6

El término 25 del AP, a ₂₅ = a + (25 – 1)d

= 7 + (24)8

= 7 + 144 

= 151

Por lo tanto, el término 25 del AP es 151.

Pregunta 42. La suma de los primeros n términos de un AP es 5n ² + 3n. Si su m ^-ésimo término es 168, encuentre el valor de m. Además, encuentre el término 20 de este AP

Solución:

Dado S _n = 5n ² + 3n,

Al poner n = 1, obtenemos el primer término(a), S ₁ = a = 5(1) ² + 3(1) = 8

Al poner n = 2 da S ₂ = a + a + d = 5(2) ² + 3(2) = 26

=> re = 26 – 2a

=> re = 26 – 16 = 10

El m ^-ésimo término del PA, a _m = a + (m – 1)d = 168

=> 8 + (m – 1)10 = 168

=> (m-1)10 = 160

=> metro – 1 = 16

=> metro = 17

20º término del AP, a ₂₀ = a + 19d

= 8 + 19(10)

= 8 + 190

= 198

Por lo tanto, el valor de m es 17 y el vigésimo término del AP es 198.

Pregunta 43. La suma de los primeros q términos de un AP es 63q – 3q ² . Si su p ^-ésimo término es –60, encuentre el valor de p. Además, encuentre el término 11 de este AP

Solución:

Dado S _n = 63q – 3q ² ,

Al poner n = 1, obtenemos el primer término(a), S ₁ = a = 63(1) – 3(1) ² = 60.

Al poner n = 2 da S ₂ = a + a + d = 63(2) – 3(2) ² = 114 

=> d = 114 – 2a

=> d = 114 – 120 = –6

El p ^-ésimo término del PA, a _p = a + (p – 1)d = –60

=> 60 + (p – 1)(–6) = –60

=> (p – 1)(–6) = –120

=> p-1 = 20

=> p = 21

11.º término del AP, a ₁₁ = a+10d

= 60 + 10(–6)

= 0

Por lo tanto, el valor de p es 21 y el término 11 de AP es 0.

Pregunta 44. La suma de los primeros m términos de un AP es 4m ² – m. Si su enésimo término es 107, encuentre el valor de n. Además, encuentre el término 21 de este AP

Solución:

Dado S _m = 4m ² – m,

Al poner m = 1, obtenemos el primer término (a), S ₁ = a = 4(1) ² – 1 = 3.

Al poner m = 2 da S ₂ = a + a + d = 4(2) ² – 2 = 14

=> re = 14 – 2a

=> re = 14 – 6 = 8

El enésimo término del AP, a _n = a + (n – 1)d = 107

=> 3 + (n – 1)8 = 107

=> 8(n – 1) = 104

=> n – 1 = 13

=> norte = 14

21° término del AP, a ₂₁ = a + 20d

= 3 + 20(8)

= 163

Por lo tanto, el valor de n es 14 y el término 21 del AP es 163.

Pregunta 45. Si la suma de los primeros n términos de un AP es 4n – n ² , ¿cuál es el primer término? ¿Cuál es la suma de los dos primeros términos? ¿Cuál es el segundo término? De manera similar, encuentre los términos 3, 10 y n.

Solución:

Dado S _n = 4n – n ² ,

Al poner n = 1, obtenemos el primer término (a), S ₁ = a = 4(1) – 1 ² = 3.

Al poner n = 2 da S ₂ = a + a + d = 4(2) – 2 ² = 4

=> re = 4 – 2a

=> d = 4 – 6 = –2

Segundo término(a ₂ ) = a + d = 3 + (–2) = 1

Usando la fórmula del enésimo término de un AP

un norte = un + ( _n – 1)d

Asi que, 

= 3 + (n – 1)(–2)

= 5 – 2n

Por lo tanto, tercer término(a ₃ ) = 5 – 2(3) = –1

Y décimo término(a ₁₀ ) = 5 – 2(10) = –15

Por lo tanto, el primer término es 3, la suma de los dos primeros términos es 4, el segundo término es 1 

y los términos 3, 10 y n son -1, -15 y 5 – 2n respectivamente.

Pregunta 46. Si la suma de los primeros n términos de un AP es 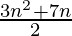  entonces encuentre su n-ésimo término. Por lo tanto, escribe su vigésimo término.

Solución:

Dado S _n = (3n ² + 7n) / 2,

Al poner n = 1, obtenemos el primer término (a), S ₁ = a = [3(1) ² + 7(1)]/2 = 10/2 = 5

Al poner n = 2 da S ₂ = a + a + d = [3(2) ² + 7(2)]/2 = 26/2 = 13

=> re = 13 – 2a

=> re = 13 – 10 = 3

Usando la fórmula del enésimo término de un AP

un norte = un + ( _n – 1)d

Asi que, 

= 5 + (n – 1)3

= 5 + 3n – 3

= 3n + 2

Ahora encontramos el vigésimo término:

₂₀ = 3 ( 20) + 2

= 60 + 2

= 62

Por lo tanto, el término n del AP dado es 3n + 2 y el término 20 es 62

Pregunta 47. En un AP la suma de los primeros n términos es 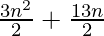 . Encuentre su término 25.

Solución:

Dado S _n = 3n ² /2 + 13n/2,

Al poner n = 1, obtenemos el primer término (a), S ₁ = a = 3(1) ² /2 + 13(1)/2 = (3 + 13) / 2 = 8

Al poner n = 2 da S ₂ = a + a + d = 3(2) ² /2+ 13(2)/2 = 19

=> re = 19 – 2a

=> re = 19 – 16 = 3

El término 25 del AP, a ₂₅ = a + (25 – 1)d

= 8 + (24)3

= 6 + 72

= 80

Por lo tanto, el término 25 del AP dado es 80.

Pregunta 48. Encuentra la suma de todos los números naturales entre 1 y 100 que son divisibles por 3.

Solución:

Los números naturales entre 1 y 100 que son divisibles por 3 son 3, 6, 9, 12, . . . 99

Estos números forman un AP con el primer término (a) = 3, 

Diferencia común (d) = 6 – 3 = 3 y n-ésimo término (a _n ) = 99.

Usando la fórmula del enésimo término de un AP

un norte = un + ( _n – 1)d

Asi que, 

=> 99 = 3 + (n – 1)3

=> 3(n – 1) = 96

=> n – 1 = 32

=> norte = 33

Usando la fórmula de la suma de los primeros n términos de un AP 

S _norte = norte [un + un _norte ] / 2.

Asi que,

S ₃₃ = 33[3 + 99]/2

= 33[51]

= 1683

Por lo tanto, la suma de todos los números naturales entre 1 y 100 que son divisibles por 3 es 1683.