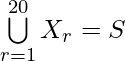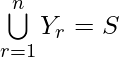Pregunta 8. Encuentra los conjuntos A, B y C, tales que A ∩ B y B ∩ C y A ∩ C son conjuntos no vacíos, y A ∩ B ∩ C = ϕ
Solución:
Consideremos los conjuntos,
A = {5, 6, 10}
B = {6, 8, 9}
C = {9, 10, 11}
Ahora tenemos,
UN ∩ segundo = 6 ≠ ϕ
segundo ∩ do = 9 ≠ ϕ
UN ∩ C = 10 ≠ ϕ
Y, A ∩ B ∩ C = ϕ
Ahora, tenemos A ∩ B y B ∩ C y A ∩ C como conjuntos no vacíos, pero A ∩ B ∩ C es un conjunto vacío.
Pregunta 9. Para cualesquiera dos conjuntos A y B, demuestre que A ∩ B = ϕ => A ⊂ B’
Solución:
Sea, a ∈ A => a ∉ B
De este modo,
UN ∩ B = ϕ
=> un ∈ B’
Así, a ∈ A y a ∈ B’ => A ⊂ B’
Pregunta 10. Demuestre lo siguiente:
(i) A – B y A ∩ B son conjuntos disjuntos
(ii) B – A y A ∩ B son conjuntos disjuntos
(iii) A – B y B – A son conjuntos disjuntos
Solución:
(i) A – B y A ∩ B
Sean a ∈ A – B => a ∈ A y a ∉ B => a ∉ A ∩ B
Por tanto, A – B y A ∩ B son conjuntos disjuntos.
(ii) Sean a ∈ B – A => a ∈ B y a ∉ A => a ∉ A ∩ B
Por tanto, B – A y A ∩ B son conjuntos disjuntos.
(iii) A-B y B-A,
A – B = x, x : x ∈ A y x ∉ B
A – B y B – A son conjuntos disjuntos.
Pregunta 11. Usando las propiedades de los conjuntos, demuestre que para dos conjuntos cualesquiera A y B,
(A ∪ B) ∩ (A ∩ B’) = A
Solución:
Tenemos,
IZQ = A ∪ B ∩ A ∩ B’
Resolviendo esto, obtenemos,
= UN ∪ segundo ∩ UN ∪ UN ∪ segundo ∩ segundo’
= UN ∪ UN ∪ B ∩ B’
Ya que, B ∩ B’ = ∅
= UN ∪ UN ∩ B’
= un
Por lo tanto, LHS = RHS.
Pregunta 12.
(i) Demuestre que para cualesquiera dos conjuntos A y B,
A’ UB = U => A ⊂ B
(ii) Demuestre que para dos conjuntos A y B cualesquiera,
B’ ⊂ A’ = U => A ⊂ B
Solución:
(i) Sea a ∈ A
= un ∈ U
= a ∈ A’ ∪ B, porque, U = A’ ∪ B
= a ∈ B, porque a ∉ A’
Por lo tanto, A ⊂ B
(ii) Sea a ∈ A
= un ∉ A’
= a ∉ B’, porque B’ es un subconjunto de A’
= un ∈ segundo
Por lo tanto, A ⊂ B
Pregunta 13. ¿Es cierto que para cualquier conjunto A y B, P(A) ∪ P(B) = P(A ∪ B)? Justifica tu respuesta.
Solución:
El resultado es Falso.
Prueba:
Sea X ∈ P(A) ∪ P(B)
= X ∈ P(A) o X ∈ P(B)
= X ⊂ A o X ⊂ B
= X ⊂ AUB
= X ∈ P(A ∩ B)
Así, P(A) ∪ P(B) ⊂ P(A ∪ B)
Además, supongamos,
X ∈ P(A ∪ B). Pero, X ∉ P(A) o X ∉ P(B)
Por ejemplo, tenemos X = 1, 2, 3, 4 y A = 2, 5 y B = 1, 3, 4.
Entonces, X ∉ P(A) ∪ P(B)
Por lo tanto, P(A ∪ B) no necesariamente tiene que ser un subconjunto de P(A) ∪ P(B).
Pregunta 14.
(i) Demuestre que para cualquier conjunto A y B,
A = (A ∩ B) ∩ (A – B)
(ii) Demuestre que para cualquier conjunto A y B,
A ∪ (B – A) = A ∪ B
Solución:
(yo) tenemos,
RHS = (A ∩ B) ∪ (A – B)
= (A ∩ B) ∪ (A ∩ B)’
= (A ∩ B) ∪ (A ∩ A) ∩ (B ∪ B)’
= UN ∩ (A ∪ B)’ ∩ (B ∪ B)’
= A ∩ (A ∪ B)’ ∩ U
= A ∩ (A ∪ B)’
= un
Por lo tanto, RHS = LHS
(ii) Tenemos,
IZQ = A ∪ (B – A)
= UN ∪ (B ∩ UN)’
= (A ∪ B) ∩ (A ∪ A)’
= (A ∪ B) ∩ U
LHS = A ∪ B = RHS
Pregunta 15. Cada conjunto X, contiene 5 elementos y cada conjunto Y, contiene 2 elementos y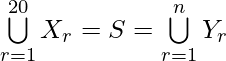 
cada elemento de S pertenece exactamente a 10 de los Xr ya exactamente 4 de Yr, luego encuentra el valor de n.
Solución:
Tenemos, Cada conjunto X contiene 5 elementos, y
Por lo tanto, n(S) = 20 x 5 = 100
Pero, sabemos, que cada uno de los elementos de S pertenecen exactamente a 10 de las X r ‘s.
Por tanto, n(S) = 100/10 = 10 -(1)
Además, Y contiene 2 elementos y
Por lo tanto, n(S) = nx 2 = 2n
Cada uno de los elementos de S pertenece exactamente a 4 de los Yr.
n(S) = 2n/4 = n/2 -(2)
De la ecuación (1) y (2)
10 = n/2
norte = 20
Publicación traducida automáticamente
Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA