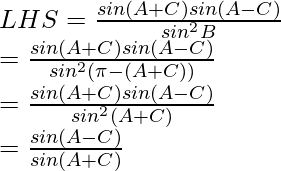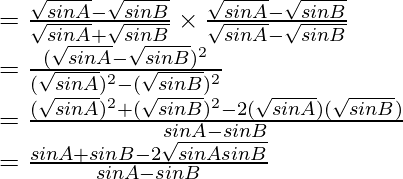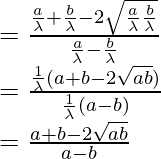Pregunta 1: Si en △ABC, ∠A=45°, ∠B=60° y ∠C=75°, encuentra la razón de sus lados.
Solución:
Según la regla del seno
Por lo tanto, obtenemos
Usando la fórmula,
sen (A+B) = sen A cos B + cos A sen B
sen (45°+30°) = sen(45°) cos(30°) + cos(45°) sen(30°)
sen 75° =
sen 75° =
Multiplicando el denominador por 2√2, obtenemos
Por lo tanto, obtenemos
un : segundo : c = 2 : √6 : (√3+1)
Pregunta 2: si en △ABC, ∠C=105°, ∠B=45° y a=2, entonces encuentra b.
Solución:
En la condición dada, ∠C=105° y ∠B=45°
Y como sabemos que,
A+B+C = π (La suma de todos los ángulos en el triángulo es suplementaria)
A = π-(B+C)
A = 180°-(45°+105°)
A = 30°
Ahora, según la regla del seno
Después de racionalizar el denominador, obtenemos
Pregunta 3: En △ABC, si a=18, b=24 y c=30 y ∠C=90°, encuentra sen A, sen B y sen C.
Solución:
En la condición dada, a=18, b=24 y c=30 y ∠C=90°
Ahora, según la regla del seno
También,
Pregunta 4: En △ABC, prueba lo siguiente:
Solución:
Según la regla del seno
Considerando la LHS de la ecuación, tenemos
Usando la fórmula trigonométrica,
sen A – sen B = 2 sen
cos
sen A + sen B = 2 sen
cos
Como, LHS = RHS
Por lo tanto, probado !!
Pregunta 5: En △ABC, prueba lo siguiente:
(ab) 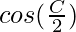 = c
= c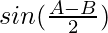
Solución:
Según la regla del seno
Considerando LHS, tenemos
Usando la fórmula trigonométrica,
sen A – sen B = 2 sen
cos
= λ
A+B+C = π (La suma de todos los ángulos en el triángulo es suplementaria)
= 2λ sen
cos
cos
= 2λ sen
cos
cos
= λ sen
(2 cos
sen
)
Usando la fórmula trigonométrica,
2 sen a cos a = sen 2a
= λ sen
( sen
)
= λ sen
sen(A+B)
= λ sen
sen(π-C) (A+B+C = π)
= λ sen
sen(C)
= (λ sen C) sen
= c pecado
Como, LHS = RHS
Por lo tanto Probado!
Pregunta 6: En △ABC, prueba lo siguiente:
Solución:
Según la regla del seno
Considerando LHS, tenemos
Usando identidades trigonométricas,
sen A – sen B = 2 sen
cos
sen 2a = 2 sen a cos a
…………………….(1)
Ahora considerando RHS, tenemos
Multiplicando en cruz obtenemos,
Usando identidades trigonométricas,
sen a cos b + cos a sen b = sen (a+b)
sen a cos b – cos a sen b = sen (ab)
…………………….(2)
Como, LHS = RHS
Por lo tanto Probado!
Pregunta 7: En △ABC, prueba lo siguiente:
Solución:
Según la regla del seno
Considerando LHS, tenemos
Usando identidades trigonométricas,
sen A + sen B = 2 sen
cos
sen 2a = 2 sen a cos a
………………………….(1)
Ahora considerando RHS, tenemos
Multiplicando en cruz obtenemos,
Usando identidades trigonométricas,
cos a cos b + sen a sen b = cos (ab)
cos a cos b – sen a sen b = cos (a+b)
…………………….(2)
Como, LHS = RHS
Por lo tanto, ¡Probado!
Pregunta 8: En △ABC, prueba lo siguiente:
Solución:
Según la regla del seno
Considerando LHS, tenemos
Usando identidades trigonométricas,
sen A + sen B = 2 sen
cos
sen 2a = 2 sen a cos a
Como, LHS = RHS
Por lo tanto, ¡Probado!
Pregunta 9: En △ABC, prueba lo siguiente:
Solución:
Según la regla del seno
Considerando RHS, tenemos
Usando identidades trigonométricas,
sen A – sen B = 2 sen
cos
Usando identidades trigonométricas,
2 sen a cos a = sen 2a
Como, LHS = RHS
Por lo tanto, ¡Probado!
Pregunta 10: En △ABC, prueba lo siguiente:
Solución:
Según la regla del seno
Considerando LHS, tenemos
Usando identidades trigonométricas,
sen 2 a – sen 2 b = sen (a+b) sen (ab)
Como, LHS = RHS
Por lo tanto, ¡Probado!
Pregunta 11: En △ABC, prueba lo siguiente:
b sen B – c sen C = a sen (BC)
Solución:
Según la regla del seno
Y, regla del coseno,
Considerando RHS, tenemos
RHS = un pecado (BC)
Usando identidades trigonométricas,
sen(ab) = sen a cos b – cos a sen b
= a (sen B cos C – cos B sen C)
= a ((bλ)
–
(cλ))
= λ
= 2λ
= λb 2 -λc 2
= b(λb) – c(λc)
= b(sen B) – c(cos C)
Como, LHS = RHS
Por lo tanto, ¡Probado!
Pregunta 12: En △ABC, prueba lo siguiente:
a 2 sen (BC) = (b 2 -c 2 ) sen A
Solución:
Según la regla del seno
Considerando RHS, tenemos
RHS = (b 2 -c 2 ) sen A
= λ 2 sen A(sen 2 B – sen 2 C)
Usando identidades trigonométricas,
sen 2 a – sen 2 b = sen (a+b) sen (ab)
= λ 2 sen A(sen(B+C) sen (BC))
= λ 2 sin A(sin(\pi-A) sin (BC))
= λ 2 sen A(sen(A) sen (BC))
= λ 2 sen 2 A sen (BC)
= (λ sen A) 2 sen (BC)
= a 2 pecado (BC)
Como, LHS = RHS
Por lo tanto, ¡Probado!
Pregunta 13: En △ABC, prueba lo siguiente:
Solución:
Considerando LHS, tenemos
IZQ =
Racionalizando el denominador, obtenemos
Según la regla del seno
Como, LHS = RHS
Por lo tanto, ¡Probado!
Pregunta 14: En △ABC, prueba lo siguiente:
a (sen B – sen C) + b(sen C – sen A) + c (sen A – sen B) = 0
Solución:
Según la regla del seno
Considerando LHS, tenemos
LHS = a (sen B – sen C) + b (sen C – sen A) + c (sen A – sen B)
= λ sin A (sin B – sin C) + λ sin B (sin C – sin A) + λ sin C (sin A – sin B)
= λ sen A sen B – λ sen A sen C+ λ sen B sen C – λ sen B sen A) + λ sen C sen A – λ sen C sen B
= 0
Como, LHS = RHS
Por lo tanto, ¡Probado!
Pregunta 15: En △ABC, prueba lo siguiente:
Solución:
Según la regla del seno
Considerando LHS, tenemos
IZQ =
=
= λ 2 sen A sen (BC) + λ 2 sen B sen (CA) + λ 2 sen C sen (AB)
Usando identidades trigonométricas,
sen(ab) = sen a cos b – cos a sen b
= λ 2 (sen A [sen B cos C – cos B sen C] + sen B [sen C cos A – cos C sen A] + sen C [sen A cos B – cos A sen B])
= λ 2 (sen A sen B cos C – sen A cos B sen C+ sen B sen C cos A – sen B cos C sen A + sen C sen A cos B – sen C cos A sen B)
= λ2 ( 0 )
= 0
Como, LHS = RHS
Por lo tanto, ¡Probado!
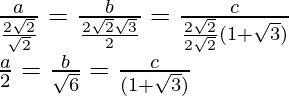
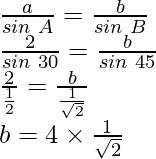
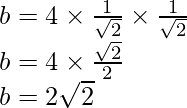
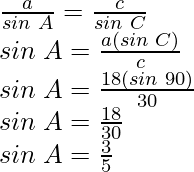
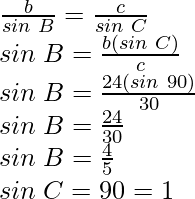
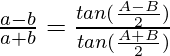
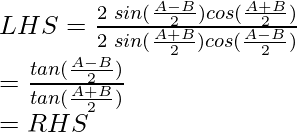
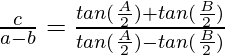
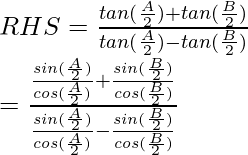
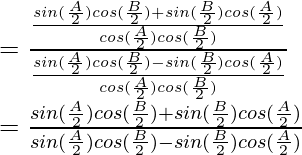
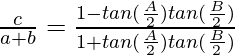
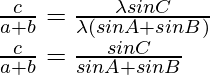
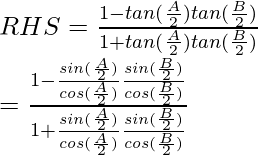
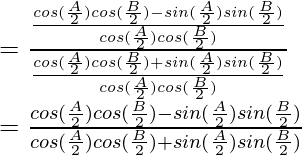
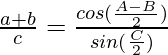
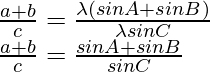
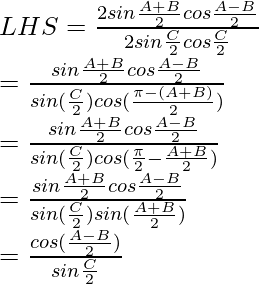
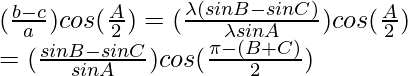
![Rendered by QuickLaTeX.com LHS = (\frac{2 sin\frac{B-C}{2}cos\frac{B+C}{2}}{sinA})cos(\frac{\pi}{2}-\frac{B+C}{2})\\ = (\frac{2 sin\frac{B-C}{2}cos\frac{B+C}{2}}{sinA})sin(\frac{B+C}{2})\\ = (\frac{[2 sin(\frac{B+C}{2}) cos\frac{B+C}{2}] sin\frac{B-C}{2}}{sinA})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e3a360aa93c71492a15cf71f8c765d64_l3.png)
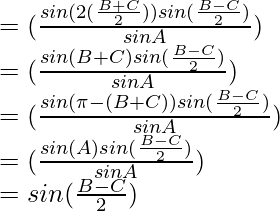
![Rendered by QuickLaTeX.com \frac{a^2-c^2}{b^2} = \frac{[\lambda sinA]^2-[\lambda sinC]^2}{[\lambda sinB]^2}\\ = \frac{(\lambda)^2 [sin^2A - sin^2C]}{(\lambda)^2[sin^2B]}\\ = \frac{sin^2A - sin^2C}{sin^2B}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bed56f4cd4175f0ba69d5daa527633fe_l3.png)