Clase 11 Soluciones RD Sharma – Capítulo 10 Fórmulas de seno y coseno y sus aplicaciones – Ejercicio 10.2 | Serie 1

Pregunta 1. En un ∆ABC, si a = 5, b = 6 y C = 60 ^o , demuestre que su área es (15√3)/2 unidades cuadradas.

Solución:

Nos dan a = 5, b = 6 y C = 60 ^o . 

Ahora sabemos que el área de un ∆ABC está dada por 1/2 ab sen C donde a y b son las longitudes de los lados de un triángulo y C es el ángulo entre estos lados.

Entonces, área de ∆ABC = (1/2) 5(6) sen 60 ^o 

= (1/2) (5) (6) (√3/2)

= 15√3/2 unidades cuadradas

Por lo tanto, probado.

Pregunta 2. En un ∆ABC, si a = √2, b = √3 yc = √5 muestra que su área es √6/2 unidades cuadradas.

Solución:

Nos dan a = √2, b = √3 y c = √5. 

Según la fórmula del coseno, cos C = (a ² + b ² – c ² )/2ab

= (2 + 3 – 5)/2√6

= 0

Entonces, sen C = √(1–cos ² C) = 1

Ahora sabemos que el área de un ∆ABC está dada por 1/2 ab sen C donde a y b son las longitudes de los lados de un triángulo y C es el ángulo entre estos lados.

Por tanto, área de ∆ABC = (1/2) (√2) (√3) (1)

= √6/2 unidades cuadradas.

Por lo tanto, probado.

Pregunta 3. Los lados de un triángulo son a = 4, b = 6 y c = 8, demuestra que: 

8 cos A + 16 cos B + 4 cos C = 17

Solución:

Nos dan a = 4, b = 6 y c = 8.

Según la fórmula del coseno, cos A = (b ² + c ² – a ² )/2bc

= (36 + 64 – 16)/96

= 84/96

= 7/8

Además, cos B = (a ² + c ² – b ² )/2ac

= (16 + 64 – 36)/64

= 44/64

= 11/16

Además, cos C = (a ² + b ² – c ² )/2ab

= (16 + 36 – 64)/48

= –12/48

= –1/4

Aquí, LHS = 8 cos A + 16 cos B + 4 cos C 

= 8 × (7/8) + 16 × (11/16) + 4 × (–1/4) 

= 7 + 11 – 1

= 17

= lado derecho

Por lo tanto, probado.

Pregunta 4. En un ∆ABC, si a = 18, b = 24, c = 30, encuentra cos A, cos B y cos C.

Solución: 

Nos dan a = 18, b = 24 y c = 30.  

Según la fórmula del coseno, cos A = (b ² + c ² – a ² )/2bc

= (24 ² + 30 ² – 18 ² )/2(24)(30)

= (576 + 900 – 324)/1440

= 1152/1440

= 4/5

Además, cos B = (a ² + c ² – b ² )/2ac

= (324 + 900 – 576)/2(18)(30)

= 648/1080

= 3/5

Además, cos C = (a ² + b ² – c ² )/2ab

= (324 + 576 – 900)/2(18)(24)

= 0

Por tanto, los valores de cos A, cos B y cos C son 4/5, 3/5 y 0 respectivamente.

Pregunta 5. Para cualquier Δ ABC, demuestre que b (c cos A – a cos C) = c ² – a ²

Solución:

Según la fórmula del coseno, 

cos A = (b ² + c ² – a ² )/2bc

=> bc cos A = (b ² + c ² – a ² )/2 . . . . (1)

Además, cos C = (a ² + b ² – c ² )/2ab

=> ab porque C = (a ² + b ² – c ² )/2 . . . . (2)

Restando (2) de (1), obtenemos,

LHS = bc cos A – ab cos C = (b ² + c ² – a ² )/2 – (a ² + b ² – c ² )/2

= (b ² + c ² – un ² – un ² – b ² + c ² )/2

= (2c ² – 2a ² )/2

= do ² – un ²

= lado derecho

Por lo tanto, probado.

Pregunta 6. Para cualquier Δ ABC, demuestre que c (a cos B – b cos A) = a ² – b ²

Solución:

Según la fórmula del coseno,

cos B = (a ² + c ² – b ² )/2ac

=> ac cos B = (a ² + c ² – b ² )/2 . . . . (1)

También cos A = (b ² + c ² – a ² )/2bc

=> bc cos A = (b ² + c ² – a ² )/2 . . . . (2)

Restando (2) de (1), obtenemos,

LHS = ac cos B – bc cos A = (a ² + c ² – b ² )/2 – (b ² + c ² – a ² )/2

= (a ² + c ² – b ² – b ² – c ² + a ² )/2  

= (2a ² – 2b ² )/2

= un ² – b ²

= lado derecho

Por lo tanto, probado.

Pregunta 7. Para cualquier Δ ABC, demuestre que 2 (bc cos A + ca cos B + ab cos C) = a ² + b ² + c ²

Solución:

Según la fórmula del coseno,

cos A = (b ² + c ² – a ² )/2bc

=> 2bc porque A = ^{segundo 2} + do ² – un ²  . . . . (1)

Además, cos B = (a ² + c ² – b ² )/2ac

=> 2ac porque segundo = un ² + c ² – ^{segundo 2} . . . . (2)

Además, cos C = (a ² + b ² – c ² )/2ab

=> 2ab porque C = un ² + ^{segundo 2} – C ² . . . . (3)

Sumando (1), (2) y (3), obtenemos,

LHS = 2bc cos A + 2ac cos B + 2ab cos C 

= ^{segundo 2} + c ² – un ² + un ² + c ² – ^{segundo 2} + un ² + ^{segundo 2} – c ²

= un ² + ^{segundo 2} + c ²

= lado derecho

Por lo tanto, probado.

Pregunta 8. Para cualquier Δ ABC, demuestre que (c ² + b ² – a ² ) tan A = (a ² + c ² – b ² ) tan B = (a ² + b ² – c ² ) tan C

Solución:

De acuerdo con la regla del seno en ΔABC,

sen A/a = sen B/b = sen C/c = k (constante) 

Según la fórmula del coseno,

cos A = (b ² + c ² – a ² )/2bc

2bc cos A = (b ² + c ² – a ² )

(b ² + c ² – a ² ) tan A = 2bc cos A tan A 

= 2bc sen A

= 2kabc. . . . (1)

Además, cos B = (a ² + c ² – b ² )/2ac

2ac cos B = (a ² + c ² – b ² )  

(a ² + c ² – b ² ) tan B = 2ac cos B tan B

= 2ac sen B

= 2kabc. . . . (2)

Además, cos C = (a ² + b ² – c ² )/2ab

2ab porque C = (a ² + b ² – c ² ) . . . . (3)

(a ² + b ² – c ² ) tan C = 2ab cos C tan C

= 2ab sen C

= 2kabc. . . . (3)

De (1), (2) y (3), obtenemos,

(c ² + b ² – a ² ) tan A = (a ² + c ² – b ² ) tan B = (a ² + b ² – c ² ) tan C

Por lo tanto, probado.

Pregunta 9. Para cualquier ΔABC, demuestre que: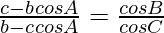 

Solución:

De acuerdo con la regla del seno en ΔABC,

a/sen A = b/sen B = c/sen C = k (constante) 

Aquí, LHS = 

= 

= 

= 

= 

= 

= 

= 

= lado derecho

Por lo tanto, probado.

Pregunta 10. Para cualquier Δ ABC demuestre que: 

a(cos B + cos C – 1) + b(cos C+ cos A – 1) + c(cos A + cos B – 1) = 0

Solución:

De acuerdo con la fórmula de proyección, obtenemos,

a = b porque C+ c porque B

b = c porque A + a porque C

c = a cos B + b cos A

Aquí, LHS = a(cos B + cos C – 1) + b(cos C+ cos A – 1) + c(cos A + cos B – 1)

= a cos B + a cos C – a + b cos C+ b cos A – b + c cos A + c cos B – c

= c – b cos A + a cos C – a + a – c cos B + b cos A – b + b – a cos C+ c cos B – c

= 0

= lado derecho

Por lo tanto, probado.