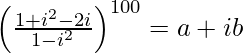Pregunta 14. Si 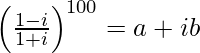 , encuentra (a, b).
, encuentra (a, b).
Solución:
Tenemos,
=>
=>
=>
=>
=> (−i) 100 = a + ib
=> a + ib = 1
Al comparar las partes real e imaginaria en ambos lados, obtenemos,
=> (a, b) = (1, 0)
Pregunta 15. Si a = cos θ + i sen θ, encuentra el valor de 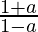 .
.
Solución:
Dado a = cos θ + i sin θ, obtenemos,
=
=
=
=
=
=
=
=
=
=
Por lo tanto, el valor de
es
.
Pregunta 16. Evalúa lo siguiente:
(i) 2x 3 + 2x 2 − 7x + 72, cuando x = (3−5i)/2
Solución:
Tenemos, x = (3−5i)/2
=> 2x = 3 − 5i
=> 2x − 3 = −5i
=> (2x − 3) 2 = 25i 2
=> 4x 2 + 9 − 12x = −25
=> 4x 2 − 12x + 34 = 0
=> 2x 2 − 6x + 17 = 0
Ahora, 2x 3 + 2x 2 − 7x + 72 = x (2x 2 − 6x + 17) + 6x 2 − 17x + 2x 2 − 7x + 72
= x (0) + 8x 2 − 24x + 72
= 4 (2x 2 – 6x + 17) + 4
= 4 (0) + 4
= 4
Por lo tanto, el valor de 2x 3 + 2x 2 − 7x + 72 es 4.
(ii) x 4 − 4x 3 + 4x 2 +8x +44, cuando x = 3 + 2i
Solución:
Tenemos, x = 3 + 2i
=> x − 3 = 2i
=> (x − 3) 2 = (2i) 2
=> x2 + 9 − 6x = 4i 2
=> x2 − 6x + 9 + 4 = 0
=> x2 − 6x + 13 = 0
Ahora, x 4 − 4x 3 + 4x 2 + 8x + 44 = x 2 (x 2 − 6x + 13) + 6x 3 − 13x 2 − 4x 3 + 4x 2 + 8x + 44
= 2x 3 − 9x 2 + 8x + 44
= 2x (x 2 – 6x + 13) + 12x 2 – 26x – 9x 2 + 8x + 44
= 3x 2 − 18x + 44
= 3 (x 2 – 6x + 13) + 5
= 5
Por lo tanto, el valor de x 4 − 4x 3 + 4x 2 + 8x + 44 es 5.
(iii) x 4 + 4x 3 + 6x 2 + 4x + 9, cuando x = −1 + i√2
Solución:
Tenemos, x = −1 + i√2
=> x + 1 = i√2
=> (x + 1) 2 = 2i 2
=> x2 + 1 + 2x = −2
=> x2 + 2x + 3 = 0
Ahora, x 4 + 4x 3 + 6x 2 + 4x + 9 = x 2 (x 2 + 2x + 3) − 2x 3 − 3x 2 + 4x 3 + 6x 2 + 4x + 9
= 2x 3 + 3x 2 + 4x + 9
= 2x (x 2 + 2x + 3) − 4x 2 − 6x + 3x 2 + 4x + 9
= − x 2 − 2x + 9
= − (x2 + 2x + 3) + 3 + 9
= 3 + 9
= 12
Por lo tanto, el valor de x 4 + 4x 3 + 6x 2 + 4x + 9 es 12.
(iv) x 6 + x 4 + x 2 + 1, cuando x = (1+i)/√2
Solución:
Tenemos, x = (1+i)/√2
=> √2x = 1 + yo
=> 2x 2 = 1 + yo 2 + 2i
=> 2x 2 = 2i
=> 4x 4 = 4i 2
=> x4 = −1
=> x4 + 1 = 0
Ahora, x 6 + x 4 + x 2 + 1 = (x 6 + x 2 ) + (x 4 +1)
= x 6 + x 2
= x2 ( x4 + 1)
= 0
Por lo tanto, el valor de x 6 + x 4 + x 2 + 1 es 0.
(v) 2x 4 + 5x 3 + 7x 2 − x + 41, cuando x = −2 − √3i
Solución:
Tenemos, x = −2 − √3i
x2 = (−2 − √3i) 2 = 4 + 4√3i + 3i 2 = 1 + 4√3i
x 3 = (1 + 4√3i) (−2 − √3i) = −2 − √3i − 8√3i −12i 2 = 10 − 9√3i
x4 = (1 + 4√3i) 2 = 1 + 8√3i + 48i 2 = −47 + 8√3i
Ahora, 2x 4 + 5x 3 + 7x 2 − x + 41 se convierte en,
= 2(−47 + 8√3i) + 5(10 − 9√3i) + 7(1 + 4√3i) − (−2 − √3i) + 41
= −94 + 16√3i + 50 − 45√3i + 7 + 28√3i + 2 + √3i + 41
= 6
Por lo tanto, el valor de 2x 4 + 5x 3 + 7x 2 − x + 41 es 6.
Pregunta 17. Para un entero positivo n, encuentre el valor de (1−i) n (1−1/i) n .
Solución:
Tenemos,
(1−i) norte (1−1/i) norte = (1−i) norte
=
=
=
= 2 norte
Por lo tanto, el valor de (1−i) n (1−1/i) n es 2 n .
Pregunta 18. Si (1+i)z = (1−i) 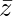 , entonces demuestre que z = −i
, entonces demuestre que z = −i 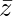 .
.
Solución:
Tenemos,
=> (1+i)z = (1−i)
=> z =
=> z =
=> z =
=> z =
=> z = −i
Por lo tanto probado.
Pregunta 19. Resuelve el sistema de ecuaciones: Re(z 2 ) = 0, |z| = 2
Solución:
Sea z = x + iy.
Ahora z 2 = (x + iy) 2
= x 2 + yo 2 y 2 + 2xyi
= x2 − y2 + 2xyi
Tenemos, Re(z 2 ) = 0
=> X 2 – y 2 = 0 . . . . (1)
Además, se da, |z| = 2
=>
= 2
=> x 2 + y 2 = 4 . . . . (2)
Resolviendo (1) y (2), obtenemos, x = ±√2 y y = ±√2.
Por lo tanto, x + iy = ±√2 ± √2i.
Pregunta 20. Si 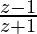 es un número puramente imaginario (z≠−1), encuentra el valor de |z|.
es un número puramente imaginario (z≠−1), encuentra el valor de |z|.
Solución:
Sea z = x + iy
Tenemos,
=
=
=
=
=
Como el número complejo es puramente imaginario, por lo tanto,
=> Re(z) = 0
=>
= 0
=> x2 + y2 = 1
=>
= 1
=> |z| = 1
Por lo tanto, el valor de |z| es 1
Pregunta 21. Si z 1 es un número complejo distinto de −1 tal que |z 1 | = 1 y z 2 = 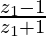 , luego demuestre que las partes reales de z 2 son cero.
, luego demuestre que las partes reales de z 2 son cero.
Solución:
Dado |z| = 1
=> |z| 2 = 1
=> x 2 + y 2 = 1 . . . . (1)
Sean z 1 = x + iy y z 2 = a + ib.
De acuerdo con la pregunta, tenemos,
=> z2 =
=> a + ib =
=> a + ib =
=> a + ib =
=> a + ib =
Usando (1) obtenemos,
=> a + ib =
=> a + ib =
Al comparar las partes real e imaginaria en ambos lados, obtenemos a = 0.
Por lo tanto, las partes reales de z 2 son 0. Por lo tanto, se demuestra.
Pregunta 22. Si |z+1| = z + 2(1+i), hallar z.
Solución:
Sea z = x + iy. De acuerdo con la pregunta, tenemos,
=> |x + iy + 1| = x + iy + 2(1 + i)
=>
= (x + 2) + i(y + 2)
Al comparar las partes real e imaginaria, obtenemos
=> y + 2 = 0
=> y = −2
Y también,
=> x + 2 =
=> (x + 2) 2 = (x+1) 2 + y 2
=> x 2 + 4 + 4x = x 2 + 2x + 1+ y 2
=> 2x = y 2 − 3
=> 2x = 4 − 3
=> 2x = 1
=> x = 1/2
Por lo tanto, z = x + iy = 1/2 −2i.
Pregunta 23. Resuelve la ecuación: |z| = z + 1 + 2i.
Solución:
Sea z = x + iy. De acuerdo con la pregunta, tenemos,
=> |z| = z + 1 + 2i
=> |x + iy| = x + iy + 1 + 2i
=>
= (x + 1) + (y + 2)i
=> x 2 + y 2 = (x+1) 2 + (y+2) 2 yo 2 + 2 (x+1) (y+2) yo
=> x2 + y2 = x2 +1 + 2x − y2 − 1 + 2y + 2 (x+1) (y+2)i
=> 2y 2 − 2x + 4y + 4 = 2i (x+1) (y+2)
=> y 2 − x + 2y + 2 = yo (x+1) (y+2)
Al comparar ambos lados, obtenemos,
=> (x+1) (y+2) = 0
=> x = −1 y y = −2
Además, y 2 − x + 2y + 2 = 0
Tomando x = −1, obtenemos y 2 − (−1) + 2y + 2 = 0
=> y 2 + 2y + 3 = 0, que no tiene solución ya que las raíces son imaginarias.
Tomando y = −2, (4 − x −4 + 2) = 0
=> x = 2
Por lo tanto, z = x + iy = 2 − 2i.
Pregunta 24. ¿Cuál es el entero positivo más pequeño n para el cual (1+i) 2n = (1−i) 2n ?
Solución:
Se nos da,
=> (1+i) 2n = (1−i) 2n
=>
= 1
=>
= 1
=>
= 1
=>
= 1
=> yo 2n = 1
=> yo 2n = yo 4
=> 2n = 4
=> norte = 2
Por lo tanto, el entero positivo más pequeño n para el cual (1+i) 2n = (1−i) 2n es 2.
Pregunta 25. Si z 1 , z 2 , z 3 son números complejos tales que |z 1 | = |z 2 | = |z 3 | = 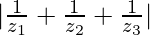 = 1, luego encuentre el valor de |z 1 + z 2 + z 3 |.
= 1, luego encuentre el valor de |z 1 + z 2 + z 3 |.
Solución:
Se nos da,
|z 1 | = |z 2 | = |z 3 | =
= 1
Ahora, |z 1 + z 2 + z 3 | =
=
=
= 1
Por lo tanto, el valor de |z 1 + z 2 + z 3 | es 1
Pregunta 26. Encuentra el número de soluciones de z 2 + |z| 2 = 0.
Solución:
Sea z = x + iy. Tenemos,
=> z2 + |z| 2 = 0
=> (x + iy) 2 + |x + iy| 2 = 0
=> x 2 + yo 2 y 2 + 2xyi + x 2 + y 2 = 0
=> x2 − y2 + 2xyi + x2 + y2 = 0
=> 2×2 + 2xyi = 0
Al comparar las partes real e imaginaria en ambos lados, obtenemos
=> 2x 2 = 0 y 2xy = 0
=> x = 0 y y ∈ R
Por tanto, z = 0 + iy, donde y ∈ R.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
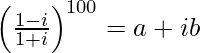
![Rendered by QuickLaTeX.com \left[\frac{(1-i)^2}{(1+i)(1-i)}\right]^{100}=a+ib](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-76713589ac91a3642b5b99d3a3ccd3ee_l3.png)