Pregunta 1. Exprese los siguientes números complejos en la forma estándar a + ib:
(yo) (1 + yo) (1 + 2i)
Solución:
Tenemos, z = (1 + i) (1 + 2i)
= 1 (1 + 2i) + yo (1 + 2i)
= 1 + 2i + yo + 2i 2
= 1 + 3i + 2(−1)
= 1 + 3i − 2
= −1 + 3i
Por lo tanto, la forma estándar es −1 + 3i donde a = −1 y b = 3.
(ii) 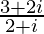
Solución:
Tenemos, z =
=
=
=
=
=
Por lo tanto, la forma estándar es
donde a = −4/5 yb = −7/5.
(iii)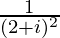
Solución:
Tenemos, z =
=
=
=
=
=
Por lo tanto, la forma estándar es
donde a = 3/25 yb = −4/25.
(iv)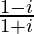
Solución:
Tenemos, z =
=
=
=
= −yo
Por lo tanto, la forma estándar es −i donde a = 0 yb = −1.
(v)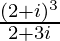
Solución:
Tenemos, z =
=
=
=
=
=
=
Por lo tanto, la forma estándar es
donde a = 37/13 yb = 16/13.
(vi)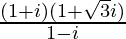
Solución:
Tenemos, z =
=
=
=
=
=
=
= –√3 + yo
Por lo tanto, la forma estándar es –√3 + i donde a = –√3 y b = 1.
(vii)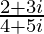
Solución:
Tenemos, z =
=
=
=
Por lo tanto, la forma estándar es
donde a = 23/41 yb = 2/41.
(viii)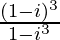
Solución:
Tenemos, z =
=
=
=
=
=
= –3 – yo
Por lo tanto, la forma estándar es –3 – i donde a = –3 y b = –1.
(ix) (1 + 2i) -3
Solución:
Tenemos z = (1 + 2i) -3
=
=
=
=
=
=
Por lo tanto, la forma estándar es
donde a = –3/13 yb = 2/13.
(X)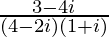
Solución:
Tenemos, z =
=
=
=
=
=
=
Por lo tanto, la forma estándar es
donde a = –1/4 yb = –3/4.
(xi)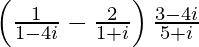
Solución:
Tenemos, z =
=
=
=
=
=
=
=
=
Por lo tanto, la forma estándar es
donde a = 478/884 yb = 928/884.
(xii)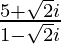
Solución:
Tenemos, z =
=
=
=
= 1+ 2√2i
Por lo tanto, la forma estándar es 1+ 2√2i donde a = 1 y b = 2√2.
Pregunta 2. Encuentra los valores reales de x e y, si
(i) (x + iy) (2 – 3i) = 4 + i
Solución:
Tenemos,
=> (x + iy) (2 – 3i) = 4 + i
=> 2x – 3xi + 2yi – 3yi 2 = 4 + yo
=> 2x + (–3x+2y)i + 3y = 4 + i
=> (2x+3y) + i(–3x+2y) = 4 + i
Al comparar las partes real e imaginaria en ambos lados, obtenemos,
2x + 3y = 4 . . . . (1)
Y –3x + 2y = 1 . . . . (2)
Al multiplicar (1) por 3 y (2) por 2 y sumar, obtenemos
=> 6x – 6x – 9y + 4y = 12 + 2
=> 13 años = 14
=> y = 14/13
Al poner y = 14/13 en (1), obtenemos
=> 2x + 3(14/13) = 4
=> 2x = 4 – (42/13)
=> 2x = 10/13
=> x = 5/13
Por tanto, los valores reales de x e y son 5/13 y 14/13 respectivamente.
(ii) (3x – 2iy) (2 + i) 2 = 10(1 + i)
Solución:
Tenemos,
=> (3x – 2iy) (2 + i) 2 = 10(1 + i)
=> (3x – 2yi) (4 + i 2 + 4i) = 10 + 10i
=> (3x – 2yi) (3 + 4i) = 10+10i
=> 3x – 2yi =
=> 3x – 2yi =
=> 3x – 2yi =
=> 3x – 2yi =
Al comparar las partes real e imaginaria en ambos lados, obtenemos,
=> 3x = 70/25 y –2y = –10/25
=> x = 70/75 y y = 1/5
Por tanto, los valores reales de x e y son 70/75 y 1/5 respectivamente.
(iii)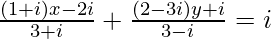
Solución:
Tenemos,
=>
=>
=>
=> (4+2i) x − 3i − 3 + (9−7i)y = 10i
=> (4x+9y−3) + i(2x−7y−3) = 10i
Al comparar las partes real e imaginaria en ambos lados, obtenemos,
4x + 9y – 3 = 0 . . . . (1)
Y 2x − 7y − 3 = 10 . . . . (2)
Al multiplicar (1) por 7 y (2) por 9 y sumando, obtenemos,
=> 28x + 18x + 63y – 63y = 117 + 21
=> 46x = 117 + 21
=> 46x = 138
=> x = 3
Al poner x = 3 en (1), obtenemos
=> 4x + 9y − 3 = 0
=> 9y = −9
=> y = −1
Por lo tanto, los valores reales de x e y son 3 y −1 respectivamente.
(iv) (1 + i) (x + iy) = 2 – 5i
Solución:
Tenemos,
=> (1 + i) (x + iy) = 2 – 5i
=> x + iy =
=> x + iy =
=> x + iy =
=> x + iy =
Al comparar las partes real e imaginaria en ambos lados, obtenemos,
=> x = −3/2 y y = −7/2
Por lo tanto, los valores reales de x e y son −3/2 y −7/2 respectivamente.
Pregunta 3. Encuentra los conjugados de los siguientes números complejos:
(yo) 4 – 5i
Solución:
Sabemos que el conjugado de un número complejo (a + ib) es (a – ib).
Por lo tanto, el conjugado de (4 – 5i) es (4 + 5i).
(ii)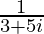
Solución:
Tenemos, z =
=
=
=
Sabemos que el conjugado de un número complejo (a + ib) es (a – ib).
Por lo tanto, el conjugado de
es
.
(iii)
Solución:
Tenemos, z =
=
=
=
Sabemos que el conjugado de un número complejo (a + ib) es (a – ib).
Por lo tanto, el conjugado de
es
.
(iv)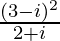
Solución:
Tenemos, z =
=
=
=
=
=
= 2 – 4i
Sabemos que el conjugado de un número complejo (a + ib) es (a – ib).
Por lo tanto, el conjugado de
es 2 + 4i.
(v)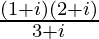
Solución:
Tenemos, z =
=
=
=
=
=
=
Sabemos que el conjugado de un número complejo (a + ib) es (a – ib).
El conjugado de
es
.
(vi)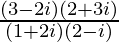
Solución:
Tenemos, z =
=
=
=
=
=
Sabemos que el conjugado de un número complejo (a + ib) es (a – ib).
Por lo tanto, el conjugado de
es
.
Pregunta 4. Encuentra el inverso multiplicativo de los siguientes números complejos:
(yo) 1 – yo
Solución:
Tenemos z = 1 – i
Sabemos que el inverso multiplicativo de un número complejo z es 1/z. Entonces, obtenemos,
=
=
=
=
Por lo tanto, el inverso multiplicativo de (1 – i) es
.
(ii) (1 + yo √3) 2
Solución:
Tenemos, z = (1 + i √3) 2
= 1 + 3i 2 + 2 i√3
= 1 + 3(−1) + 2 i√3
= 1 – 3 + 2 i√3
= −2 + 2 i√3
Sabemos que el inverso multiplicativo de un número complejo z es 1/z. Entonces, obtenemos,
=
=
=
=
=
Por lo tanto, el inverso multiplicativo de (1 + i √3) 2 es
.
(iii) 4 – 3i
Solución:
Tenemos z = 4 – 3i
Sabemos que el inverso multiplicativo de un número complejo z es 1/z. Entonces, obtenemos,
=
=
=
=
Por lo tanto, el inverso multiplicativo de 4 – 3i es
.
(iv) √5 + 3i
Solución:
Tenemos z = √5 + 3i
Sabemos que el inverso multiplicativo de un número complejo z es 1/z. Entonces, obtenemos,
=
=
=
=
Por lo tanto, el inverso multiplicativo de √5 + 3i es
.
Pregunta 5. Si z 1 = 2 − i, z 2 = 1 + i, encuentra 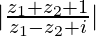 .
.
Solución:
Dado z 1 = 2 − i, z 2 = 1 + i, obtenemos,
=
=
=
=
= 2√2
Por lo tanto, el valor de
es 2√2.
Pregunta 6. Si z 1 = (2 – i), z 2 = (–2 + i), encuentra
(i) Re
Solución:
Dado z 1 = (2 – i), z 2 = (–2 + i), obtenemos,
=
=
=
=
=
=
=
Por lo tanto, Re
=
.
(ii) soy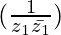
Ahora,
=
=
=
=
=
Por lo tanto, Im
= 0.
Pregunta 7. Encuentra el módulo de 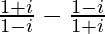 .
.
Solución:
Tenemos, z =
=
=
=
= 2i
Entonces, módulo de z =
= 2.
Por lo tanto, el módulo de
es 2.
Pregunta 8. Si x + iy = 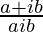 , demuestre que x 2 + y 2 = 1.
, demuestre que x 2 + y 2 = 1.
Solución:
Tenemos,
=> x + iy =
Al aplicar módulo en ambos lados obtenemos,
=> |x + iy| =
=> |x + iy| =
=>
=>
= 1
=> x2 + y2 = 1
Por lo tanto probado.
Pregunta 9. Encuentra el valor integral mínimo positivo de n para el cual ![Rendered by QuickLaTeX.com \left[\frac{1+i}{1-i}\right]^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c8645087921c320291ee1c71ccf3d648_l3.png) es real.
es real.
Solución:
Tenemos, z =
=
=
=
= yo norte
Para n = 2, tenemos i n = i 2 = −1, que es real
Por tanto, el menor valor integral positivo de n para el cual
es real es 2.
Pregunta 10. Encuentra los valores reales de θ para los cuales el número complejo 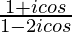 es puramente real.
es puramente real.
Solución:
Tenemos, z =
=
=
=
=
Para que un número complejo sea puramente real, la parte imaginaria debe ser igual a cero.
Entonces, obtenemos,
= 0
=> cos θ = 0
=> cos θ = cos π/2
=> 2nπ ± π/2, para n ∈ Z
Por tanto, los valores de θ para que el número complejo sea puramente real son 2nπ ± π/2, para n ∈ Z.
Pregunta 11. Encuentra el valor entero positivo más pequeño de n para el cual 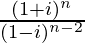 es un número real.
es un número real.
Solución:
Tenemos, z =
=
=
=
=
=
=
= yo norte × (−2i )
= −2i n+1
Para n = 1, tenemos z = −2i 1+1
= −2i 2
= 2, que es real
Por lo tanto, el valor entero positivo más pequeño de n para el cual es un número real
es 1.
Pregunta 12. Si 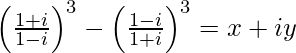 , encuentra (x, y).
, encuentra (x, y).
Solución:
Tenemos,
=>
=>
=>
=> i 3 – (–i 3 ) = x + iy
=> 2i 3 = x + iy
=> x + iy = −2i
Al comparar las partes real e imaginaria en ambos lados, obtenemos,
=> (x, y) = (0, −2)
Pregunta 13. Si 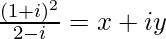 , encuentra x + y.
, encuentra x + y.
Solución:
Tenemos,
=>
=>
=>
=>
=>
Al comparar las partes real e imaginaria en ambos lados, obtenemos,
=> x = −2/5 y y = 4/5
Entonces, x + y = −2/5 + 4/5
= (−2+4)/5
= 2/5
Por lo tanto, el valor de (x + y) es 2/5.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
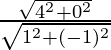
![Rendered by QuickLaTeX.com \left[\frac{(1+i)^2}{(1-i)(1+i)}\right]^3-\left[\frac{(1-i)^2}{(1+i)(1-i)}\right]^3=x+iy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9602a571223758c3c80bc9c8507ad7b2_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{1+i^2+2i}{1-i^2}\right]^3-\left[\frac{1+i^2-2i}{1-i^2}\right]^3=x+iy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0d988d3c1ecd473deacf0be32db917a9_l3.png)