Clase 11 Soluciones RD Sharma – Capítulo 28 Introducción a la geometría de coordenadas 3D – Ejercicio 28.2

Pregunta 1. Encuentra la distancia entre los siguientes pares de puntos:

(i) P(1, −1, 0) y Q (2, 1, 2)

Solución:

Dado: Los puntos P(1, −1, 0) y Q(2, 1, 2)

Al usar la fórmula de distancia, la distancia entre dos puntos (a, b, c) y (d, e, f) se da de la siguiente manera:

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

Por lo tanto, la distancia entre P(1, −1, 0) y Q(2, 1, 2) viene dada por,

$\sqrt{(1 − 2)^2 + (−1 −1)^2 + (0 − 2)^2}$

= $\sqrt{(−1)^2 + (− 2)^2 + (− 2)^2}$

= $\sqrt{(1 + 4 + 4)}$

= $\sqrt{9}$

= 3

∴ La Distancia entre P y Q es de 3 unidades.

(ii) A (3, 2, −1) y B (−1, −1, −1)

Solución:

Dado: Los puntos A (3, 2, −1) y B (−1, −1, −1)

Al usar la fórmula de distancia, la distancia entre dos puntos (a, b, c) y (d, e, f) viene dada por:

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

Por lo tanto, la distancia entre A (3, 2, −1) y B (−1, −1, −1) viene dada por,

$\sqrt{(3 − (−1))^2 + (2 − (−1))^2 + (−1 − (−1))^2}$

= $\sqrt{(3 + 1)^2 + (2 + 1)^2 + (−1 + 1)^2}$

= $\sqrt{(4^2 + 3^2 + 0^2)}$

= $\sqrt{25}$

= 5

∴ La Distancia entre A y B es de 5 unidades.

Pregunta 2. Encuentra la distancia entre los puntos P y Q que tienen coordenadas (−2, 3, 1) y (2, 1, 2).

Solución:

Dado: Los puntos P(− 2, 3, 1) y Q(2, 1, 2)

Al usar la fórmula de la distancia, la distancia entre dos puntos (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

Por lo tanto, la distancia entre P(−2, 3, 1) y Q(2, 1, 2) viene dada por,

$\sqrt{(−2 − 2)^2 + (3 − 1)^2 + (1 − 2)^2}$

= $\sqrt{(−4)^2 + 2^2 +(−1)^2}$

= $\sqrt{21}$

∴ La distancia entre los dos puntos dados es $\sqrt{21}$ unidades.

Pregunta 3. Usando la fórmula de la distancia, demuestre que los siguientes puntos son colineales:

(i) A(4, −3, −1), B(5, −7, 6) y C(3, 1, −8)

Solución:

Dado: Los puntos A(4, −3, −1), B(5, −7, 6) y C(3, 1, −8)

Los puntos A, B y C son colineales si AB + BC = AC o AB + AC = BC o AC+ BC = AB

Usando la fórmula, la distancia entre dos puntos cualesquiera (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

Por lo tanto, la distancia entre A(4, −3, −1) y B(5, −7, 6) viene dada por,

AB = $\sqrt{(4 − 5)^2 + (−3 −(−7))^2 + (−1 − 6)^2}$

= $\sqrt{(−1)^2 + (−4)^2 + (−7)^2}$

AB = $\sqrt{66}$

Ahora, la distancia entre B(5, −7, 6) y C(3, 1, −8) viene dada por,

BC = $\sqrt{(5 − 3)^2 + (−7 − 1)^2 + ( 6 − (−8))^2}$

= $\sqrt{(2)^2 + (−8)^2 + (14)^2}$

BC = 2 $\sqrt{66}$

Además, la distancia entre A(4, −3, −1) y C(3, 1, −8) viene dada por,

CA = $\sqrt{(4 − 3)^2 + (−3 − 1)^2 + ( −1 − (−8))^2}$

= $\sqrt{(1)^2 + (−4)^2 + (7)^2}$

CA = $\sqrt{66}$

Claramente, AB + AC = $\sqrt{66}$ + $\sqrt{66}$ = 2 $\sqrt{66}$ = BC

∴Los puntos A, B y C son colineales.

(ii) P (0, 7, -7), Q (1, 4, -5) y R (-1, 10, -9)

Solución:

Dado: Los puntos P (0, 7, −7), Q (1, 4, −5) y R (−1, 10, −9)

Los puntos P, Q y R son colineales si PQ + QR = PR o PQ + PR = QR o PR + QR = PQ

Usando la fórmula, la distancia entre dos puntos cualesquiera (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

Por lo tanto, la distancia entre P (0, 7, −7), Q (1, 4, −5) viene dada por,

PQ = $\sqrt{(0 − 1)^2 + (7 − 4)^2 + (−7 − (−5)^2}$

= $\sqrt{(−1)^2 + (3)^2 + (−2)^2}$

PQ = $\sqrt{14}$

Ahora, la distancia entre Q (1, 4, −5) y R (−1, 10, −9) viene dada por,

QR = $\sqrt{(1 − (−1))^2 + (4 − 10)^2 + (−5 − (−9))^2}$

= $\sqrt{(2)^2 + (−6)^2 + (4)^2}$

QR = 2 $\sqrt{14}$

Además, la distancia entre P (0, 7, −7) y R (−1, 10, −9) viene dada por,

PR = $\sqrt{(0 − ( −1))^2 + (7 − 10)^2 + ( −7 − (−9))^2}$

= $\sqrt{(1)^2 + (−3)^2 + (2)^2}$

PR= $\sqrt{14}$

Claramente, PQ+ PR= $\sqrt{14}$ + $\sqrt{14}$ = 2 $\sqrt{14}$ = QR

∴Los puntos P, Q y R son colineales.

(iii) A(3, -5, 1), B(-1, 0, 8) y C(7, -10, -6)

Solución:

Dado: Los puntos A(3, -5, 1), B(-1, 0, 8) y C(7, -10, -6)

Los puntos A, B y C son colineales si AB + BC = AC o AB + AC = BC o AC+ BC = AB

Usando la fórmula, la distancia entre dos puntos cualesquiera (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

Por lo tanto, la distancia entre A(3, -5, 1) y B (-1, 0, 8) viene dada por,

AB = $\sqrt{(3 − (-1))^2 + (−5 −0)^2 + (1 − 8)^2}$

= $\sqrt{(4)^2 + (−5)^2 + (−7)^2}$

AB = $\sqrt{90}$

Ahora, la distancia entre B(-1, 0, 8) y C(7, -10, -6) viene dada por,

BC = $\sqrt{(-1− 7)^2 + (0 + 10)^2 + (6 + 8)^2}$

= $\sqrt{(-8)^2 + (10)^2 + (14)^2}$

= $\sqrt{360} = \sqrt{4 × 90}$

BC = $2 \sqrt{90}$

Además, la distancia entre A(3, -5, 1) y C(7, -10, -6) viene dada por,

CA = $\sqrt{(3 − 7)^2 + (−5 + 10)^2 + ( 1 + 6)^2}$

= $\sqrt{(-4)^2 + (5)^2 + (7)^2}$

$AC = \sqrt{90}$

Claramente, AB + AC = $\sqrt{90} + \sqrt{90} = 2 \sqrt{90}$ = BC

∴Los puntos A, B y C son colineales.

Pregunta 4. Determina los puntos en los que equidistan de los puntos A(1, -1, 0), B(2, 1, 2) y C(3, 2, -1) en

(i) plano xy

Solución:

Dado: Los puntos A(1, -1, 0), B(2, 1, 2) y C(3, 2, -1)

Sabemos que z = 0 en el plano xy. Sea P(x, y, 0) cualquier punto en el plano xy

Nos dan: PA = PB = PC

⇒ PA ² = PB ² = CP ²

Usando la fórmula, la distancia entre dos puntos cualesquiera (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

Sabemos PA ² = PB ²

Entonces, (x – 1) ² + (y + 1) ² = (x – 2) ² + (y – 1) ² + 4

⇒ x ² + 1 – 2x + y ² + 1 + 2y = x ² + 4 – 4x + y ² + 1 – 2y + 4

⇒ – 2x + 2 + 2y = 9 – 4x – 2y

⇒ – 2x + 2 + 2y – 9 + 4x + 2y = 0

⇒ 2x + 4y – 7 = 0

⇒ 2x = – 4y + 7 ……(a)

Ya que, PA ² = PC ²

Entonces, (x – 1) ² + (y + 1) ² = (x – 3) ² + (y – 2) ² + 1

⇒ x ² + 1 – 2x + y ² + 1 + 2y = x ² + 9 – 6x + y ² + 4 – 4y + 1

⇒ – 2x + 2 + 2y = 14 – 6x – 4y

⇒ – 2x + 2 + 2y – 14 + 6x + 4y = 0

⇒ 4x + 6y – 12 = 0

⇒ 2(2x + 3y – 6) = 0

Ahora sustituimos el valor de 2x (obtenido en la ecuación (a)), obtenemos

7 – 4 años + 3 años – 6 = 0

⇒ – y + 1 = 0 ⇒ y = 1

Sustituyendo el valor de y en la ecuación (a) obtenemos,

2x = 7 – 4y

⇒ 2x = 7 – 4(1)

⇒ 2x = 3 ⇒ x = 3/2

∴El punto P (3/2, 1, 0) en el plano xy es equidistante de A, B y C.

(ii) plano yz

Solución:

Sabemos que x = 0 en el plano yz. Sea Q(0, y, z) cualquier punto en el plano yz

Según la pregunta: QA = QB = QC

⇒ QA ² = QB ² = QC ²

Usando la fórmula, la distancia entre dos puntos cualesquiera (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

Sabemos, QA ² = QB ²

Entonces, 1 + z ² + (y + 1) ² = (z – 2) ² + (y – 1) ² + 4

⇒ z ² + 1 + y ² + 1 + 2y = z ² + 4 – 4z + y ² + 1 – 2y + 4

⇒ 2 + 2y = 9 – 4z – 2y

⇒ 2 + 2y – 9 + 4z + 2y = 0

⇒ 4y + 4z – 7 = 0

⇒ 4z = –4y + 7

$⇒ z = \frac{-4y + 7}{4}$ ……. (1)

Ya que, QA ² = QC ²

Entonces, 1 + z ² + (y + 1) ² = (z + 1) ² + (y – 2) ² + 9

⇒ 2+ 1 + y ² + 1 + 2y = z ² + 1 + 2z + y ² + 4 – 4y + 9

⇒ 2 + 2y = 14 + 2z – 4y

⇒ 2 + 2y – 14 – 2z + 4y = 0

⇒ –2z + 6y – 12 = 0

⇒ 2(–z + 3y – 6) = 0

Sustituyendo el valor de z [obtenido de (1)] obtenemos:

12 años + 4 años – 7 – 24 = 0

⇒ 16y – 31 = 0 ⇒ y = 31/16

Sustituyendo el valor de y en la ecuación (1), obtenemos z = -3/16

∴El punto Q (0, 31/16, -3/16) en el plano yz es equidistante de A, B y C.

(iii) plano zx

Solución:

Sabemos y = 0 en el plano xz. Sea R(x, 0, z) cualquier punto en el plano xz

Según la pregunta: RA = RB = RC

⇒ RA ² = RB ² = RC ²

Usando la fórmula, la distancia entre dos puntos cualesquiera (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

Sabemos, RA ² = RB ²

Entonces, 1 + z ² + (x – 1) ² = (z – 2) ² + (x – 2) ² + 1

⇒ z ² + 1 + x ² + 1 – 2x = z ² + 4 – 4z + x ² + 4 – 4x + 1

⇒ 2 – 2x = 9 – 4z – 4x

⇒ 2 + 4z – 9 + 4x – 2x = 0

⇒ 2x + 4z – 7 = 0

⇒ 2x = –4z + 7 …………(1)

Ya que, RA ² = RC ²

Entonces, 1 + z ² + (x – 1) ² = (z + 1) ² + (x – 3) ² + 4

⇒ z ² + 1 + x ² + 1 – 2x = z ² + 1 + 2z + x ² + 9 – 6x + 4

⇒ 2 – 2x = 14 + 2z – 6x

⇒ 2 – 2x – 14 – 2z + 6x = 0

⇒ –2z + 4x – 12 = 0

⇒ 2(2x) = 12 + 2z

Sustituyendo el valor de 2x [obtenido de la ecuación (1)] obtenemos,

2(–4z + 7) = 12 + 2z

⇒ –8z + 14 = 12 + 2z

⇒ 14 – 12 = 8z + 2z

⇒ 10z = 2 ⇒ z = 2/10 = 1/5

Ahora, reemplazando el valor de z en la ecuación (1), obtenemos 2x = -4z + 7

⇒ x = -4/5 +7 = 31/10

∴El punto R (31/10, 0, 1/5) en el plano xz es equidistante de A, B y C.

Pregunta 5. Determine el punto en el eje z que es equidistante de los puntos (1, 5, 7) y (5, 1, -4)

Solución:

Dado: Los puntos (1, 5, 7) y (5, 1, -4)

Sabemos que x = 0 y y = 0 en el eje z. Sea R(0, 0, z) cualquier punto en el eje z

Según la pregunta: RA = RB

⇒ RA ² = RB ²

Usando la fórmula, la distancia entre dos puntos cualesquiera (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

Sabemos, RA ² = RB ²

⇒ 26+ (z – 7) ² = (z + 4) ² + 26

⇒ z2 ⁺ 49 – 14z + 26 = z2 + 16 + 8z + ²⁶

⇒ 49 – 14z = 16 + 8z

⇒ 49 – 16 = 14z + 8z

⇒ 22z = 33

⇒ z = 33/22

⇒ z= 3/2

∴El punto R (0, 0, 3/2) en el eje z es equidistante de (1, 5, 7) y (5, 1, -4).

Pregunta 6. Encuentra el punto en el eje y que es equidistante de los puntos (3, 1, 2) y (5, 5, 2).

Solución:

Dado: Los puntos (3, 1, 2) y (5, 5, 2)

Sabemos x = 0 y z = 0 en el eje y. Sea R(0, y, 0) cualquier punto en el eje y

Según la pregunta: RA = RB

⇒ RA ² = RB ²

Usando la fórmula, la distancia entre dos puntos cualesquiera (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

Sabemos, RA ² = RB ²

⇒ 13+ (y – 1) ² = (y – 5) ² + 29

⇒ ^y2 + 1 – 2y + 13 = ^y2 + 25 – 10y + 29

⇒ 10 años – 2 años = 54 – 14

⇒ 8 años = 40

⇒ y = 40/8 = 5

∴El punto R (0, 5, 0) en el eje y es equidistante de (3, 1, 2) y (5, 5, 2).

Pregunta 7. Encuentra los puntos en el eje z que están a una distancia 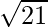$\sqrt{21}$ del punto (1, 2, 3).

Solución:

Dado: El punto (1, 2, 3) y Distancia = $\sqrt{21}$

Sabemos que x = 0 y y = 0 en el eje z. Sea R(0, 0, z) cualquier punto en el eje z

Según pregunta:

AR = $\sqrt{21}$

⇒ AR ² = 21

Usando la fórmula, la distancia entre dos puntos cualesquiera (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

Soluciones de RD Sharma para Matemáticas de Clase 11 Capítulo 28 – imagen 25

Sabemos, RA ² = 21

⇒ 5 + (z – 3) ² = 21

⇒ z2 + 9 – 6z + 5 = ²¹

⇒ z ² – 6z = 21 – 14

⇒ z ² – 6z – 7 = 0

⇒z ² – 7z + z – 7 = 0

⇒ z(z–7) + 1(z–7) = 0

⇒ (z– 7) (z + 1) = 0

⇒ (z– 7) = 0 o (z + 1) = 0

⇒ z= 7 o z = -1

∴Los puntos (0, 0, 7) y (0, 0, -1) en el eje z son equidistantes de (1, 2, 3).

Pregunta 8. Demostrar que el triángulo formado por la unión de los tres puntos cuyas coordenadas son (1, 2, 3), (2, 3, 1) y (3, 1, 2) es un triángulo equilátero.

Solución:

Dado: Los puntos A(1, 2, 3), B(2, 3, 1) y C(3, 1, 2)

Sabemos que un triángulo equilátero es un triángulo cuyos lados son todos iguales.

Así que probemos AB = BC = AC.

Usando la fórmula, la distancia entre dos puntos cualesquiera (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

Entonces, la distancia entre A(1, 2, 3) y B(2, 3, 1) viene dada por:

$AB = \sqrt{(1 − 2)^2 + (2 − 3)^2 + (3 − 1)^2}$

⇒ $AB = \sqrt{6}$

La distancia entre B(2, 3, 1) y C(3, 1, 2) viene dada por:

$BC = \sqrt{(2 − 3)^2 + (3 − 1)^2 + (1 − 2)^2}$

⇒ $BC = \sqrt{6}$

La distancia entre A(1, 2, 3) y C(3, 1, 2) viene dada por:

$AC = \sqrt{(1 − 3)^2 + (2 − 1)^2 + (3 − 2)^2}$

⇒ $AC= \sqrt{6}$

Es claro que, AB = BC = AC = $\sqrt{6}$

Δ ABC es un triángulo equilátero.

Pregunta 9. Demuestre que los puntos (0, 7, 10), (-1, 6, 6) y (-4, 9, 6) son los vértices de un triángulo rectángulo isósceles.

Solución:

Dado: Los puntos A(0, 7, 10), B(-1, 6, 6) y C(-4, 9, 6).

Usando la fórmula, la distancia entre dos puntos cualesquiera (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

AB = $\sqrt{(0 + 1)^2 + (7 − 6)^2 + (10 − 6)^2}$

⇒ AB = $\sqrt{18}$

⇒ $AB = 3\sqrt{2}$

$BC = \sqrt{-1 + 4)^2 + (6 − 9)^2 + (6 − 6)^2}$

⇒ $BC = \sqrt{18}$

⇒ $BC = 3\sqrt{2}$

$AC = \sqrt{0 + 4)^2 + (7 − 9)^2 + (10 − 6)^2}$

⇒ $AC = \sqrt{36}$

⇒ CA = 6

Ya que, AB = BC

Entonces, AB ² + BC ² = $(3\sqrt{2})^2 + (3\sqrt{2})^2$

= 18 + 18 = 36

⇒ AB ² + BC ² = AC ²

Sabemos que, AB = BC y AB ² + BC ² = AC ²

Entonces, Δ ABC es un triángulo rectángulo isósceles.

Pregunta 10. Demuestra que los puntos A(3, 3, 3), B(0, 6, 3), C(1, 7, 7) y D(4, 4, 7) son los vértices de cuadrados.

Solución:

Dado: Los puntos A (3, 3, 3), B (0, 6, 3), C (1, 7, 7) y D (4, 4, 7)

Sabemos que todos los lados de un cuadrado son iguales.

Usando la fórmula, la distancia entre dos puntos cualesquiera (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

⇒ $AB = \sqrt{(3 − 0)^2 + (3 − 6)^2 + (3 − 3)^2}$

= $\sqrt{18}$

$BC = \sqrt{(0 − 1)^2 + (6 − 7)^2 + (3 − 7)^2}$

= $\sqrt{18}$

$CD = \sqrt{(1 − 4)^2 + (7 − 4)^2 + (7 − 7)^2}$

= $\sqrt{18}$

$AD = \sqrt{(3 − 4)^2 + (3 − 4)^2 + (3 − 7)^2}$

= $\sqrt{18}$

Es claro que, AB = BC = CD = AD = $3\sqrt{2}$

El cuadrilátero formado por ABCD es un cuadrado. [Ya que todos los lados son iguales]

Pregunta 11. Demuestra que los puntos A(1, 3, 0), B(-5, 5, 2), C(-9, -1, 2) y D(-3, -3, 0) tomados en orden son los vértices de un paralelogramo. Además, demuestre que ABCD no es un rectángulo.

Solución:

Dado: Los puntos A (1, 3, 0), B (-5, 5, 2), C (-9, -1, 2) y D (-3, -3, 0)

Sabemos que los lados opuestos del paralelogramo y del rectángulo son iguales.

Pero las diagonales de un paralelogramo no son iguales mientras que son iguales para un rectángulo.

Usando la fórmula, la distancia entre dos puntos cualesquiera (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

$AB = \sqrt{(1 + 5)^2 + (3 − 5)^2 + (0 − 2)^2}$

= $\sqrt{44}$

$BC = \sqrt{(-5 + 9)^2 + (5 + 1)^2 + (2 − 2)^2}$

$= \sqrt{52}$

$CD = \sqrt{(-9 + 3)^2 + (-1 + 3)^2 + (2 − 0)^2}$

$=\sqrt{44}$

$AD = \sqrt{(1 + 3)^2 + (3 + 3)^2 + (0 − 0)^2}$

$= \sqrt{52}$

Es claro que, AB = CD y BC = AD

Los lados opuestos son iguales. Ahora encontremos la longitud de las diagonales

Usando la fórmula,

$AC = \sqrt{(1 + 9)^2 + (3 + 1)^2 + (0 − 2)^2}$

$= \sqrt{120}$

$BD = \sqrt{(-5 + 3)^2 + (3 + 5)^2 + (0 − 2)^2}$

$= \sqrt{72}$

Es claro que, AC ≠ BD

Las diagonales no son iguales, pero los lados opuestos son iguales.

Entonces podemos decir que el cuadrilátero formado por ABCD es un paralelogramo pero no un rectángulo.

Pregunta 12. Demuestra que los puntos A(1, 3, 4), B(-1, 6, 10), C(-7, 4, 7) y D(-5, 1, 1) son los vértices de un rombo.

Solución:

Dado: Los puntos A (1, 3, 4), B (-1, 6, 10), C (-7, 4, 7) y D (-5, 1, 1)

Sabemos que todos los lados del cuadrado y del rombo son iguales.

Usando la fórmula, la distancia entre dos puntos cualesquiera (a, b, c) y (d, e, f) viene dada por,

$\sqrt{(a − d)^2 + (b − e)^2 + (c − f)^2}$

AB = $\sqrt{(1 + 1)^2 + (3 − 6)^2 + (4 − 10)^2}$

$= \sqrt{49} = 7$

$BC = \sqrt{(-1 + 7)^2 + (6 − 4)^2 + (10 − 7)^2}$

$= \sqrt{49} = 7$

$CD = \sqrt{(-7 + 5)^2 + (4 − 1)^2 + (7 − 1)^2}$

$= \sqrt{49} = 7$

$AD = \sqrt{(1 + 5)^2 + (3 − 1)^2 + (4 − 1)^2}$

$= \sqrt{49} = 7$

Es claro que, AB = BC = CD = AD

Entonces, todos los lados son iguales.

Ahora, encontremos la longitud de las diagonales. Usando la fórmula,

$AC = \sqrt{(1 + 7)^2 + (3 + 4)^2 + (4 + 7)^2}$

$= \sqrt{234}$

$BD = \sqrt{(-1 + 5)^2 + (6 − 1)^2 + (10 − 1)^2}$

$= \sqrt{122}$

Es claro que, AC ≠ BD

Las diagonales no son iguales, pero todos los lados son iguales.

Entonces podemos decir que el cuadrilátero formado por ABCD es un rombo.

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 11 Soluciones RD Sharma – Capítulo 28 Introducción a la geometría de coordenadas 3D – Ejercicio 28.2 | Serie 1

Pregunta 1. Encuentra la distancia entre los siguientes pares de puntos:

(i) P(1, −1, 0) y Q (2, 1, 2)

(ii) A (3, 2, −1) y B (−1, −1, −1)

Pregunta 2. Encuentra la distancia entre los puntos P y Q que tienen coordenadas (−2, 3, 1) y (2, 1, 2).

Pregunta 3. Usando la fórmula de la distancia, demuestre que los siguientes puntos son colineales:

(i) A(4, −3, −1), B(5, −7, 6) y C(3, 1, −8)

(ii) P (0, 7, -7), Q (1, 4, -5) y R (-1, 10, -9)

(iii) A(3, -5, 1), B(-1, 0, 8) y C(7, -10, -6)

Pregunta 4. Determina los puntos en los que equidistan de los puntos A(1, -1, 0), B(2, 1, 2) y C(3, 2, -1) en

(i) plano xy

(ii) plano yz

(iii) plano zx

Pregunta 5. Determine el punto en el eje z que es equidistante de los puntos (1, 5, 7) y (5, 1, -4)

Pregunta 6. Encuentra el punto en el eje y que es equidistante de los puntos (3, 1, 2) y (5, 5, 2).

Pregunta 7. Encuentra los puntos en el eje z que están a una distancia $\sqrt{21}$ del punto (1, 2, 3).

Pregunta 8. Demostrar que el triángulo formado por la unión de los tres puntos cuyas coordenadas son (1, 2, 3), (2, 3, 1) y (3, 1, 2) es un triángulo equilátero.

Pregunta 9. Demuestre que los puntos (0, 7, 10), (-1, 6, 6) y (-4, 9, 6) son los vértices de un triángulo rectángulo isósceles.

Pregunta 10. Demuestra que los puntos A(3, 3, 3), B(0, 6, 3), C(1, 7, 7) y D(4, 4, 7) son los vértices de cuadrados.

Pregunta 11. Demuestra que los puntos A(1, 3, 0), B(-5, 5, 2), C(-9, -1, 2) y D(-3, -3, 0) tomados en orden son los vértices de un paralelogramo. Además, demuestre que ABCD no es un rectángulo.

Pregunta 12. Demuestra que los puntos A(1, 3, 4), B(-1, 6, 10), C(-7, 4, 7) y D(-5, 1, 1) son los vértices de un rombo.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra la distancia entre los siguientes pares de puntos:

(i) P(1, −1, 0) y Q (2, 1, 2)

(ii) A (3, 2, −1) y B (−1, −1, −1)

Pregunta 2. Encuentra la distancia entre los puntos P y Q que tienen coordenadas (−2, 3, 1) y (2, 1, 2).

Pregunta 3. Usando la fórmula de la distancia, demuestre que los siguientes puntos son colineales:

(i) A(4, −3, −1), B(5, −7, 6) y C(3, 1, −8)

(ii) P (0, 7, -7), Q (1, 4, -5) y R (-1, 10, -9)

(iii) A(3, -5, 1), B(-1, 0, 8) y C(7, -10, -6)

Pregunta 4. Determina los puntos en los que equidistan de los puntos A(1, -1, 0), B(2, 1, 2) y C(3, 2, -1) en

(i) plano xy

(ii) plano yz

(iii) plano zx

Pregunta 5. Determine el punto en el eje z que es equidistante de los puntos (1, 5, 7) y (5, 1, -4)

Pregunta 6. Encuentra el punto en el eje y que es equidistante de los puntos (3, 1, 2) y (5, 5, 2).

Pregunta 7. Encuentra los puntos en el eje z que están a una distancia del punto (1, 2, 3).

Pregunta 8. Demostrar que el triángulo formado por la unión de los tres puntos cuyas coordenadas son (1, 2, 3), (2, 3, 1) y (3, 1, 2) es un triángulo equilátero.

Pregunta 9. Demuestre que los puntos (0, 7, 10), (-1, 6, 6) y (-4, 9, 6) son los vértices de un triángulo rectángulo isósceles.

Pregunta 10. Demuestra que los puntos A(3, 3, 3), B(0, 6, 3), C(1, 7, 7) y D(4, 4, 7) son los vértices de cuadrados.

Pregunta 11. Demuestra que los puntos A(1, 3, 0), B(-5, 5, 2), C(-9, -1, 2) y D(-3, -3, 0) tomados en orden son los vértices de un paralelogramo. Además, demuestre que ABCD no es un rectángulo.

Pregunta 12. Demuestra que los puntos A(1, 3, 4), B(-1, 6, 10), C(-7, 4, 7) y D(-5, 1, 1) son los vértices de un rombo.

Deja una respuesta Cancelar la respuesta

Pregunta 7. Encuentra los puntos en el eje z que están a una distancia $\sqrt{21}$ del punto (1, 2, 3).