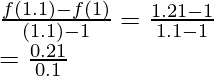Pregunta 10. Si f, g, h son tres funciones definidas de R a R como sigue:
(yo) f(x) = x 2
(ii) g(x) = senx
(iii) h(x) = x2 + 1
Encuentra el rango de cada función.
Solución:
(yo) tenemos,
f(x) = x2
Rango de f(x) = R+ (conjunto de todos los números reales mayores o iguales a cero)
= {x ∈ R+ | X ≥ 0}
(ii) Tenemos
g(x) = senx
Rango de g(x) = {x ∈ R : -1 ≤ x ≤ 1}
(iii) Tenemos
h(x) = x2 + 1
Rango de h(x) = {x ∈ R : x ≥ 1}
Pregunta 11. Sean X = {1, 2, 3, 4} e Y = {1, 5, 9, 11, 15, 16}
Determine cuáles de los siguientes conjuntos son funciones de X a Y
(a) f 1 = {(1, 1), (2, 11), (3, 1), (4, 15)}
(b) f = {(1, 1), (2, 7), (3, 5)}
(c) f = {(1,5), (2, 9), (3, 1), (4, 5), (2, 11)}
Solución:
(a) Tenemos,
f 1 = {(1, 1), (2, 11), (3, 1), (4, 15)}
f 1 es una función de X a Y
(b) Tenemos,
f 2 = {(1, 1), (2, 7), (3, 5)}
f 2 no es una función de X a Y porque hay un elemento 4 ∈ x que no está asociado a ningún elemento de Y.
c) Tenemos,
f 3 = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
f 3 no es una función de X a Y porque un elemento 2 ∈ x está asociado a dos elementos 9 y 11 en Y.
Pregunta 12. Sean A = {12, 13, 14, 15, 16, 17} y f : A ⇢ Z una función dada por f(x) = máximo factor primo de x. Encuentre el rango de f.
Solución:
Tenemos,
f(x) = factor primo más alto de x.
Por lo tanto,
12 = 3 × 4,
13 = 13 × 1,
14 = 7 × 2,
15 = 5 × 3,
16 = 2 × 8,
17 = 17 × 1
Por lo tanto,
f = {(12, 3), (13, 3), (14, 7), (15, 5), (16, 2), (17, 17)}
Rango (f) = {3, 13, 7, 5, 2, 17}
Pregunta 13. Si f : R ⇢ R se define por f(x) = x 2 + 1, entonces encuentra f -1 {17} y f -1 {-3}.
Solución:
Lo sabemos,
si f : A ⇢ 13
tal que y ∈ 3. Entonces,
f -1 (y) = {x ∈ A : f(x) = y}. En otras palabras, f -1 (y) es el conjunto de preimágenes de y.
Sea f -1 (17) = x. Entonces, f(x) = 17
⇒x2 + 1 = 17
⇒x2 = 17 – 1 = 16
⇒ x = ±4
Sea f -1 {-3} = x. Entonces, f(x) = -3
⇒x2 + 1 = -3
⇒x2 = -3 – 1 = -4
⇒ x =
Por lo tanto, f-1 {-3} = 0
Pregunta 14. Sean A = {p, q, r, s} y B = {1, 2, 3}. ¿Cuál de las siguientes relaciones de A a B no es una función?
(a) R 1 = R 1 = {(p, 1), (q, 2), (r, 1), (s, 2)}
(b) R 2 = {(p, 1), (q, 1), (r, 1), (s, 2)}
(c) R 3 = {(p, 1), (q, 2), (p, 2), (s, 3)}
(d) R 4 = {(p, 2), (q, 3), (r, 2), (s, 2)}
Solución:
Tenemos
A = {p, q, r, s} y B = {1, 2, 3}
(a) Ahora,
R 1 = {(p, 1), (q, 2), (r, 1), (s, 2)}
R 1 es una función
(b) Ahora,
R 2 = {(p, 1), (q, 2), (r, 1), (s, 1)}
R 2 es una función
c) Ahora,
R 3 = {(p, 2), (q, 3), (r, 2), (s, 2)}
R 3 no es una función porque un elemento p ∈ A está asociado a dos elementos 1 y 2 en B.
(d) Ahora,
R 4 = {(p, 2), (q, 3), (r, 2), (s, 2)}
R 4 es una función
Pregunta 15. Sea A = {9, 10, 11, 12, 13} y sea f : A ⇢ N definida por f(n) = el factor primo más alto de n. Encuentre el rango de f.
Solución:
Tenemos,
f(n) = el factor primo más alto de n.
Ahora,
9 = 3 × 3,
10 = 5 × 2,
11 = 11 × 1,
12 = 3 × 4,
13 = 13 × 1
Por lo tanto,
f = {(9, 3), (10, 5), (11, 11), (12, 3), (13, 13)}
Claramente, rango (f) = {3, 5, 11, 13}
Pregunta 16. La función f está definida por
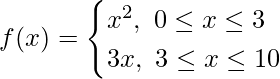
La relación f está definida por
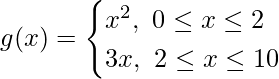
Demostrar que f es una función y g no es una función
Solución:
Tenemos,
y,
Ahora, f(3) = (3) 2 = 9 y f(3) = 3 × 3 = 9
y, g(2) = (2) 2 = 4 y g(2) = 3 × 2 = 6
Observamos que f(x) toma un valor único en cada punto de su dominio [0,10]. Sin embargo, g(x) no toma un valor único en cada punto de su dominio [0, 10].
Por tanto, g(x) no es una función.
Pregunta 17. Si f(x) = x 2 , encuentra
![]()
Solución:
Dado f(x) = x 2
f(1,1) = 1,21
f(1) = 1
= 2,1
Pregunta 18. Expresar la función f : X ⇢ R dada por f(x) = x 3 + 1 como conjunto de pares ordenados, donde x = {-1, 0, 3, 9, 7}.
Solución:
f : X ⇢ R dada por f(x) = x 3 + 1
f(-1) = (-1) 3 + 1 = -1 + 1 = 0
f(0) = (0) 3 + 1 = 0 + 1 = 1
f(3) = (3) 3 + 1 = 27 + 1 = 28
f(9) = (9) 3 + 1 = 81 + 1 = 82
f(7) = (7) 3 + 1 = 343 + 1 = 344
El conjunto de pares ordenados son {(-1, 0), (0, 1), (3, 28), (9, 82), (7, 344)}
Publicación traducida automáticamente
Artículo escrito por yashkumar0457 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA