Pregunta 1. Defina una función como un conjunto de pares ordenados.
Solución:
Sean A y B dos conjuntos no vacíos. Una relación de A a B, es decir, un subconjunto de A×B, se denomina función (o aplicación) de A a B, si
(i) para cada a ∈ A existe b ∈ B tal que (a, b) ∈ f
(ii) (a, b) ∈ f y (a, c) ∈ f ⇒ b = c
Pregunta 2. Defina una función como una correspondencia entre dos conjuntos.
Solución:
Sean A y B dos conjuntos no vacíos. Entonces una función ‘f’ del conjunto A al B es una regla o método o correspondencia que asocia elementos del conjunto A a elementos del conjunto B tal que:
(i) todos los elementos del conjunto A están asociados a elementos del conjunto B.
(ii) un elemento del conjunto A está asociado a un único elemento del conjunto B.
Pregunta 3. ¿Cuál es la diferencia fundamental entre una relación y una función? ¿Toda relación es una función?
Solución:
Sea ‘f’ una función y R una relación definida del conjunto X al conjunto Y.
El dominio de la relación R puede ser un subconjunto del conjunto X, pero el dominio de la función f debe ser igual a X. Esto se debe a que cada elemento del dominio de una función debe tener un elemento asociado, mientras que este es no es necesario para una relación.
En relación, un elemento de X puede estar asociado con uno o más elementos de Y, mientras que debe estar asociado con un solo elemento de Y en una función.
Por lo tanto, no toda relación es una función. Sin embargo, toda función es necesariamente una relación.
Pregunta 4. Sean A = {–2, –1, 0, 1, 2} y f: A → Z una función definida por f(x) = x 2 – 2x – 3. Halla:
(i) rango de f es decir f (A)
(ii) preimágenes de 6, –3 y 5
Solución:
Dado:
A = {–2, –1, 0, 1, 2}
f : A → Z tal que f(x) = x 2 – 2x – 3
(i) Rango de f ie f (A)
A es el dominio de la función f. Por tanto, rango es el conjunto de elementos f(x) para todo x ∈ A.
Sustituyendo x = –2 en f(x), obtenemos
f(–2) = (–2) 2 – 2(–2) – 3
= 4 + 4 – 3
= 5
Sustituyendo x = –1 en f(x), obtenemos
f(–1) = (–1) 2 – 2(–1) – 3
= 1 + 2 – 3
= 0
Sustituyendo x = 0 en f(x), obtenemos
f(0) = (0) 2 – 2(0) – 3
= 0 – 0 – 3
= – 3
Sustituyendo x = 1 en f(x), obtenemos
f(1) = 1 2 – 2(1) – 3
= 1 – 2 – 3
= – 4
Sustituyendo x = 2 en f(x), obtenemos
f(2) = 2 2 – 2(2) – 3
= 4 – 4 – 3
= –3
Por lo tanto, el rango de f es {-4, -3, 0, 5}.
(ii) preimágenes de 6, –3 y 5
Sea x la preimagen de 6
⇒ f(x) = 6
x 2 – 2x – 3 = 6
x 2 – 2x – 9 = 0
x = [-(-2) ± √ ((-2) 2 – 4(1) (-9))] / 2(1)
= [2 ± √ (4+36)] / 2
= [2 ± √40] / 2
= 1 ± √10
Sin embargo, 1 ± √10 ∉ A
Por lo tanto, no existe una preimagen de 6.
Ahora, sea x la preimagen de –3
⇒ f(x) = –3
x2 – 2x – 3 = –3
x2 – 2x = 0
x(x-2) = 0
x = 0 o 2
Claramente, tanto 0 como 2 son elementos de A.
Así, 0 y 2 son las preimágenes de –3.
Ahora, sea x la preimagen de 5
⇒ f(x) = 5
x 2 – 2x – 3 = 5
x 2 – 2x – 8 = 0
x 2 – 4x + 2x – 8= 0
x(x-4) + 2(x-4) = 0
(x + 2)(x – 4) = 0
x = –2 o 4
Sin embargo, 4 ∉ A pero –2 ∈ A
Por lo tanto, –2 son las preimágenes de 5.
∴ Ø, {0, 2}, -2 son las preimágenes de 6, -3, 5
Pregunta 5. Si una función f: R → R se define por
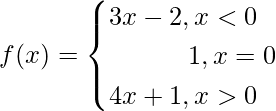
Encuentre: f (1), f (–1), f (0), f (2).
Solución:
Dado:
Encontremos f (1), f (–1), f (0) y f (2).
Cuando x > 0, f (x) = 4x + 1
Sustituyendo x = 1 en la ecuación anterior, obtenemos
f(1) = 4(1) + 1
= 4 + 1
= 5
Cuando x < 0, f(x) = 3x – 2
Sustituyendo x = –1 en la ecuación anterior, obtenemos
f (–1) = 3(–1) – 2
= –3 – 2
= –5
Cuando x = 0, f(x) = 1
Sustituyendo x = 0 en la ecuación anterior, obtenemos
f(0) = 1
Cuando x > 0, f(x) = 4x + 1
Sustituyendo x = 2 en la ecuación anterior, obtenemos
f(2) = 4(2) + 1
= 8 + 1
= 9
∴ f (1) = 5, f (–1) = –5, f (0) = 1 y f (2) = 9.
Pregunta 6. Una función f: R → R está definida por f(x) = x 2 . Determinar
(i) rango de f
(ii) {x: f(x) = 4}
(iii) {y: f(y) = –1}
Solución:
Dado:
F : R → R y f(x) = X 2 .
(i) rango de f
Dominio de f = R (conjunto de números reales)
Sabemos que el cuadrado de un número real siempre es positivo o igual a cero.
∴ rango de f = R + ∪ {0}
(ii) {x: f(x) = 4}
Dado:
f(x) = 4
sabemos, x 2 = 4
x 2 – 4 = 0
(x – 2)(x + 2) = 0
∴ x = ± 2
∴ {x: f(x) = 4} = {–2, 2}
(iii) {y: f(y) = –1}
Dado:
f(y) = –1
y2 = –1
Sin embargo, el dominio de f es R, y para todo número real y, el valor de y 2 no es negativo.
Por lo tanto, no existe y real para el cual y 2 = –1.
∴{y: f(y) = –1} = ∅
Pregunta 7. Sea f: R + → R, donde R + es el conjunto de todos los números reales positivos, tal que f(x) = log e x. Determinar
(i) el conjunto de imágenes del dominio de f
(ii) {x: f (x) = –2}
(iii) si se cumple f (xy) = f (x) + f (y).
Solución:
Dado f: R+→ R y f(x) = log e x.
(i) el conjunto de imágenes del dominio de f
Dominio de f = R + (conjunto de números reales positivos)
Sabemos que el valor del logaritmo en base e (logaritmo natural) puede tomar todos los valores reales posibles.
∴ El conjunto de imágenes de f = R
(ii) {x: f(x) = –2}
Dado f(x) = –2
log e x = –2
∴ x = e -2 [ya que, log b a = c ⇒ a = bc]
∴ {x: f(x) = –2} = {e- 2 }
(iii) Si se cumple f (xy) = f (x) + f (y).
Tenemos f (x) = log e x ⇒ f (y) = log e y
Ahora, consideremos f (xy)
F (xy) = log e (xy)
f (xy) = log e (x × y) [ya que, log b (a×c) = log b a + log b c]
f (xy) = log e x + log e y
f (xy) = f (x) + f (y)
∴ se cumple la ecuación f (xy) = f (x) + f (y).
Pregunta 8. Escribe las siguientes relaciones como conjuntos de pares ordenados y encuentra cuáles de ellos son funciones:
(i) {(x, y): y = 3x, x ∈ {1, 2, 3}, y ∈ {3, 6, 9, 12}}
(ii) {(x, y): y > x + 1, x = 1, 2 y y = 2, 4, 6}
(iii) {(x, y): x + y = 3, x, y ∈ {0, 1, 2, 3}}
Solución:
(i) {(x, y): y = 3x, x ∈ {1, 2, 3}, y ∈ {3, 6, 9, 12}}
Cuando x = 1, y = 3(1) = 3
Cuando x = 2, y = 3(2) = 6
Cuando x = 3, y = 3(3) = 9
∴ R = {(1, 3), (2, 6), (3, 9)}
Por lo tanto, la relación dada R es una función.
(ii) {(x, y): y > x + 1, x = 1, 2 y y = 2, 4, 6}
Cuando x = 1, y > 1 + 1 o y > 2 ⇒ y = {4, 6}
Cuando x = 2, y > 2 + 1 o y > 3 ⇒ y = {4, 6}
∴ R = {(1, 4), (1, 6), (2, 4), (2, 6)}
Por lo tanto, la relación dada R no es una función.
(iii) {(x, y): x + y = 3, x, y ∈ {0, 1, 2, 3}}
Cuando x = 0, 0 + y = 3 ⇒ y = 3
Cuando x = 1, 1 + y = 3 ⇒ y = 2
Cuando x = 2, 2 + y = 3 ⇒ y = 1
Cuando x = 3, 3 + y = 3 ⇒ y = 0
∴ R = {(0, 3), (1, 2), (2, 1), (3, 0)}
Por lo tanto, la relación dada R es una función.
Pregunta 9. Sean f: R → R y g: C → C dos funciones definidas como f(x) = x 2 y g(x) = x 2 . ¿Son funciones iguales?
Solución:
Dado:
f: R → R ∈ f(x) = x 2 y g : R → R ∈ g(x) = x 2
f se define de R a R, el dominio de f = R.
g se define de C a C, el dominio de g = C.
Dos funciones son iguales solo cuando el dominio y el codominio de ambas funciones son iguales.
En este caso, el dominio de f ≠ dominio de g.
∴ f y g no son funciones iguales.
Publicación traducida automáticamente
Artículo escrito por yashkumar0457 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA