Pregunta 27. Si y = [log{x+(√x 2 +1)}] 2 , demuestre que (1 + x 2 )(d 2 y/dx 2 ) + x(dy/dx) = 2.
Solución:
Tenemos,
y = [log{x + (√x 2 + 1)}] 2
dy/dx = 2[log{x + (√x 2 + 1)}]/(√x 2 + 1)
(x 2 + 1) (d 2 y/dx 2 ) = 2 – x (dy/dx)
(x 2 + 1) (d 2 y/dx 2 ) + x (dy/dx) = 2
Pregunta 28. Si y = (tan -1 x) 2 , entonces demuestre que (1 + x 2 ) 2 y 2 + 2x(1 + x 2 )y 1 = 2
Solución:
Tenemos,
y = (tan -1 x) 2
y 1 = 2(tan -1 x)[1/(1 + x 2 )]
(1 + x 2 )y 1 = 2(tan -1 x)
(1 + x 2 )y 2 + 2xy 1 = 2/(1 + x 2 )
(1 + x 2 ) 2 y 2 + 2x (1 + x 2 ) y 1 = 2
Pregunta 29. Si y = cotx, demuestre que (d 2 y/dx 2 ) + 2y(dy/dx) = 0.
Solución:
Tenemos,
y = cotx
(dy/dx) = -coseg 2 x
d 2 y/dx 2 = -(2cosec x) × (-cosec x.cot x)
d 2 y/dx 2 = 2cosec 2 x.cot x
d 2 y/dx 2 = 2(cot x)(cosec 2 x)
d 2 y/dx 2 = -2y(dy/dx)
d 2 y/dx 2 + 2y(dy/dx) = 0
Por lo tanto probado
Pregunta 30. Encuentra d 2 y/dx 2 donde y = log(x 2 /e 2 ).
Solución:
Tenemos,
y = log(x 2 /e 2 )
(dy/dx) = (2/x)
d 2 y/dx 2 = -(2/x 2 )
Por lo tanto probado
Pregunta 31. Si y = ae 2x + be -x , demuestre que (d 2 y/dx 2 ) – (dy/dx) – 2y = 0.
Solución:
Tenemos,
y = ae 2x + be -x
yo,
(dy/dx) = 2ae 2x – ser -x
(d 2 y/dx 2 ) = 4ae 2x + be -x
(d 2 y/dx 2 ) = 2ae 2x – ser -x + 2(ae 2x + ser -x )
(d 2 y/dx 2 ) = (dy/dx) + 2y
(d 2 y/dx 2 ) – (dy/dx) – 2y = 0
Por lo tanto probado
Pregunta 32. Si y = e x (senx + cosx), demuestre que d 2 y/dx 2 – 2(dy/dx) + 2y = 0.
Solución:
Tenemos,
y = e x (senx + cosx)
(dy/dx) = e x (senx + cosx) + e x (cosx – senx)
(dy/dx) = 2e x cosx
(d 2 y/dx 2 ) = 2e x cosx – 2e x senx
Tomemos LHS,
= d 2 y/dx 2 – 2(dy/dx) + 2y
= 2e x cosx – 2e x senx – 2(2e x cosx) + 2e x (senx + cosx)
= 4e x cosx – 4e x cosx – 2e x senx + 2e x senx
= 0
LHS = RHS
Por lo tanto probado
Pregunta 33. Si y = cos -1 x, encuentre d 2 y/dx 2 en términos de y solo.
Solución:
Tenemos,
y = cos -1 x
(dy/dx) = -1/√(1-x 2 )
…(i)
y = cos -1 x
x = acogedor
Al poner el valor de x en la ecuación (i), obtenemos
d 2 y/dx 2 = -cosy/sen 3 y
d 2 y/dx 2 = -cot y cosec 2 y
Pregunta 34. Si y = 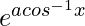 , demuestre que (1 – x 2 )(d 2 y/dx 2 ) – x(dy/dx) – a 2 y = 0.
, demuestre que (1 – x 2 )(d 2 y/dx 2 ) – x(dy/dx) – a 2 y = 0.
Solución:
Tenemos,
y =
Tomando registro de ambos lados
logía = acos -1 x.loge
logía = acos -1 x
(1/y)(dy/dx) = a×[-1/√(1-x 2 )]
(dy/dx) = -ay/√(1-x 2 )
Al elevar al cuadrado ambos lados, tenemos
(dy/dx) 2 = a 2 y 2 /(1 – x 2 )
(1 – x 2 )(dy/dx) 2 = a 2 y 2
2(1 – x 2 )(dy/dx)(d 2 y/dx 2 ) – 2x(dy/dx) 2 = 2a 2 y(dy/dx)
(1 – x 2 )(d 2 y/dx 2 ) – x(dy/dx) = a 2 y
(1 – x 2 )(d 2 y/dx 2 ) – x(dy/dx) – a 2 y = 0
Por lo tanto probado
Pregunta 35. Si y = 500e 7x + 600e -7x , demuestre que d 2 y/dx 2 = 49y.
Solución:
Tenemos,
y = 500e 7x + 600e -7x
θ,
(dy/dx) = 7 × (500e 7x – 600e -7x )
(d 2 y/dx 2 ) = 49 × (500e 7x + 600e -7x )
(d2y / dx2 ) = 49y
Por lo tanto probado
Pregunta 36. Si x = 2cos t – cos 2t, y = 2sen t – sen 2t, encuentre d 2 y/dx 2 en t = π/2.
Solución:
Tenemos,
x = 2cos t – cos 2t, y y = 2sen t – sen 2t
yo,
(dx/dt) = -2sen t + 2sen 2t, (dy/dt) = 2cos t – 2cos 2t
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = (2cos t – 2cos 2t)/(-2sen t + 2sen 2t)
(dy/dx) = (cos t – cos 2t)/(-sen t + sen 2t)
En t = π/2
d 2 y/dx 2 = (1 + 2)/-2
d 2 y/dx 2 = -(3/2)
Pregunta 37. Si x = 4z 2 + 5, y = 6z 2 + 7z + 3, encuentre d 2 y/dx 2 .
Solución:
Tenemos,
x = 4z 2 + 5, y y = 6z 2 + 7z + 3
z,
(dx/dz) = 8z, y (dy/dz) = 12z + 7
(dy/dx) = (dy/dz) × (dz/dx)
(dy/dx) = (12z + 7)/8z
(d 2 y/dx 2 ) = -7/64z 3
Por lo tanto probado
Pregunta 38. Si y = log(1 + cosx), demuestre que d 3 y/dx 3 + (d 2 y/dx 2 ).(dy/dx) = 0.
Solución:
Tenemos,
y = log(1 + cosx)
(dy/dx) = -senx/(1 + cosx)
d 2 y/dx 2 = (-cosx – cos 2 x – sen 2 x)/(1 + cosx) 2
d 2 y/dx 2 = -(1 + cosx)/(1 + cosx) 2
d 2 y/dx 2 = -1/(1 + cosx)
d 3 y/dx 3 = -senx/(1 + cosx) 2
d 3 y/dx 3 + [-1/(1 + cosx)][-senx/(1 + cosx)] = 0
d 3 y/dx 3 + (d 2 y/dx 2 ).(dy/dx) = 0
Por lo tanto probado
Pregunta 39. Si y = sin(logx), demuestre que x 2 (d 2 y/dx 2 ) + x(dy/dx) + y = 0.
Solución:
Tenemos,
y = sen(logx)
(dy/dx) = cos(logx).(1/x)
x(dy/dx) = cos(logx)
x(d 2 y/dx 2 ) + (dy/dx) = -sen(logx).(1/x)
x 2 (d 2 y/dx 2 ) + x(dy/dx) = -sin(logx)
x 2 (d 2 y/dx 2 ) + x(dy/dx) = -y
x 2 (d 2 y/dx 2 ) + x(dy/dx) + y = 0
Por lo tanto probado
Pregunta 40. Si y = 3e 2x + 2e 3x , demuestre que d 2 y/dx 2 – 5(dy/dx) + 6y = 0.
Solución:
Tenemos,
y = 3e 2x + 2e 3x
(dy/dx) = 6e 2x + 6e 3x
(dy/dx) = 6(e 2x + e 3x )
d 2 y/dx 2 = 6(2e 2x + 3e 3x )
d 2 y/dx 2 = 12e 2x + 18e 3x
d 2 y/dx 2 = 5(6e 2x + 6e 3x ) – 6(3e 2x + 2e 3x )
d 2 y/dx 2 = 5(dy/dx) – 6y
d 2 y/dx 2 – 5(dy/dx) + 6y = 0
Por lo tanto probado
Pregunta 41. Si y = (cot -1 x) 2 , demuestre que y 2 (x 2 + 1) 2 + 2x(x 2 + 1)y 1 = 2.
Solución:
Tenemos,
y = (cuna -1 x) 2
y 1 = 2(cuna -1 x) × [-1/(1 + x 2 )]
(1 + x 2 )y 1 = -2cot -1 x
(1 + x 2 )y 2 + 2xy 1 = 2/(1 + x 2 )
(1 + x 2 ) 2 y 2 + 2x (1 + x 2 ) y 1 = 2
Por lo tanto probado
Pregunta 42. Si y = cosec -1 x, entonces demuestre que x(x 2 – 1)d 2 y/dx 2 – (2x 2 – 1)(dy/dx) = 0.
Solución:
Tenemos,
y = cosec -1 x
(dy/dx) = -1/x√(x 2 – 1)
Al cuadrar ambos lados,
(dy/dx) 2 = 1/x 2 (x 2 – 1)
x 2 (x 2 – 1) (dy/x) 2 = 1
(x 4 – x 2 )(dy/dx) 2 = 1
2(dy/dx)(d 2 y/dx 2 )(x 4 – x 2 ) + (dy/dx) 2 (4x 3 – 2x) = 0
2x 2 (x 2 – 1)(dy/dx)(d 2 y/dx 2 ) + 2x(2x 2 – 1)(dy/dx) 2 = 0
x(x 2 – 1)(d 2 y/dx 2 ) + (2x 2 – 1)(dy/dx) = 0
Por lo tanto probado
Pregunta 43. Si x = cos t + log(tant/2), y = sen t, entonces encuentre el valor de d 2 y/dt 2 y d 2 y/dx 2 en t = π/4 en términos de y solo .
Solución:
Tenemos,
y = sen t
yo,
(dy/dt) = cos t
(d 2 y/dx 2 ) = -sen t
En t = π/4
(d 2 y/dx 2 ) t=π/4 = -sen(π/4)
= -1/√2
x = cos t + log(tant/2)
yo,
(dx/dt) = -sen t + (1/sen t)
(dx/dt) = (-sen 2 t + 1)/sen t
(dx/dt) = cos 2 t/sint
(dx/dt) = cos t × cot t
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = [cos t] × [1/cos t × cot t]
(dy/dx) = tan t
(d 2 y/dx 2 ) = seg 2 t × (dt/dx)
(d 2 y/dx 2 ) = seg 2 t × [1/cos t × cot t]
(d 2 y/dx 2 ) = sen t/cos 4 t
(d 2 y/dx 2 ) t=π/4 = sen(π/4)/cos 4 (π/4)
(d 2 y/dx 2 ) = 2√2
En t = π/4, (d 2 y/dx 2 ) = -1/√2 y (d 2 y/dx 2 ) = 2√2
Pregunta 44. Si x = asen t, y = a[cos t + log(tant/2)], encuentre d 2 y/dx 2 .
Solución:
Tenemos,
x = asen t, y y = a[cos t + log(tant/2)]
yo,
(dx/dt) = acos t y
(dy/dt) = a[-sen t + (1/sen t)]
(dy/dt) = a[(-sen 2 t + 1)/sen t]
(dy/dt) = a[cos 2 t/sint]
(dy/dt) = acos t × cot t
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = [acos t × cot t] × [1/acos t]
(dy/dx) = cuna t
(d 2 y/dx 2 )=-coseg 2 t × (dt/dx)
(d 2 y/dx 2 ) = -cosec 2 t × [1/acos t]
(d 2 y/dx 2 ) = -(1/asen 2 t × cos t)
Pregunta 45. Si x = a(cos t + tsen t), y y = a(sen t – tcos t), entonces encuentre el valor de d 2 y /dx 2 en t = π/4.
Solución:
Tenemos,
x = a(cos t + tsen t), y y = a(sen t – tcos t)
yo,
(dx/dt) = a(-sen t + sen t + tcos t)
(dx/dt) = atcos t
y = a(sen t – tcos t)
yo,
(dy/dx) = a(cos t – cos t + tsen t)
(dy/dx) = en sen t
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = [atsen t] × [1/atcos t]
(dy/dx) = tan t
(d 2 y/dx 2 ) = segundo 2 x × (dt/dx)
(d 2 y/dx 2 ) = seg 2 x × (1/atcos t)
(d 2 y/dx 2 ) = 1/atcos 3 t
(d 2 y/dx 2 ) = (8√2/aπ)
Pregunta 46. Si x = a[cos t + log(tant/2)], y = asin t, evalúe (d 2 y/dx 2 ) en t = π/3.
Solución:
Tenemos,
y = asen t
yo,
(dy/dt) = acos t
x = a[cos t + log(tant/2)]
yo,
(dx/dt) = a[-sen t + (1/sen t)]
(dx/dt) = a[(-sen 2 t + 1)/sen t]
(dx/dt) = a[cos 2 t/sint]
(dx/dt) = acos t × cot t
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = [cos t] × [1/cos t × cot t]
(dy/dx) = tan t
(d 2 y/dx 2 ) = seg 2 t × (dt/dx)
(d 2 y/dx 2 ) = sec 2 t × [1/acos t × cot t]
(d 2 y/dx 2 ) = sen t/acos 4 t
(d 2 y/dx 2 ) t=π/3 = sin(π/3)/acos 4 (π/3)
(d 2 y/dx 2 ) = (8√3/a)
Pregunta 47. Si x = a(cos2t + 2tsen2t) y y = a(sen2t – 2tcos2t), entonces encuentre d 2 y/dx 2 .
Solución:
Tenemos,
x = a(cos2t + 2tsen2t), y y = a(sen2t – 2tcos2t)
yo,
(dx/dt) = a(-2sen2t + 2sen2t + 4tcos2t), y (dy/dt) = a(2cos2t – 2cos2t + 4tsen2t)
(dy/dt) = a(4tcos2t), y (dy/dt)=a(4tsen2t)
(dy/dx) = (dy/dz) × (dz/dx)
(dy/dx) = a(4tsen2t)/a(4tcos2t)
(dy/dx) = tan2t
(d 2 y/dx 2 ) = 2 seg 2 2t.(dt/dx)
(d 2 y/dx 2 ) = 2 s 2 2 t/4 atcos 2 t
(d 2 y/dx 2 ) = 1/2 atcos 3 2t
(d 2 y/dx 2 ) = (1/2 en) × (seg 3 x)
Pregunta 48. Si x = asen t – bcos t, y = acos t + bsen t, demuestre que (d 2 y/dx 2 ) = -(x 2 + y 2 )/y 3
Solución:
Tenemos,
x = asen t – b cos t
yo,
(dx/dt) = acos t + bsen t
y = acos t + b sen t
yo,
(dy/dt) = -asin t + bcos t
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = [-asin t + bcos t] × [1/(acos t + bsen t)]
d 2 y/dx 2 = (-y 2 – x 2 )/y 3
re 2 y/dx 2 = -(x 2 + y 2 )/y 3
Por lo tanto probado
Pregunta 49. Encuentra A y B para que y = Asen3x + Bcos3x, satisfaga la ecuación d 2 y/dx 2 + 4(dy/dx) + 3y = 10cos3x.
Solución:
Tenemos,
y = Asen3x + Bcos3x,
(dy/dx) = 3Acos3x – 3Bsen3x
d 2 y/dx 2 = -9Asen3x – 9Bcos3x
d 2 y/dx 2 + 4(dy/dx) + 3y = (-9Asen3x – 9Bcos3x) + 4(3Acos3x – 3Bsen3x) + 3(Asen3x + Bcos3x)
= -9Asen3x – 9Bcos3x + 12Acos3x – 12Bsen3x + 3Asen3x + 3Bcos3x
= -6Asen3x – 12Bsen3x – 6Bcos3x + 12Acos3x
= (-6A – 12B)sen3x + (-6B + 12A)cos3x …(i)
Dado que
d 2 y/dx 2 + 4(dy/dx) + 3y = 10 cos 3x …(ii)
Al comparar los coeficientes, obtenemos
(-6A – 12B) = 0 y (-6B + 12A) = 10
Resolviendo ecuación,
A = (2/3) y B = -(1/3)
Pregunta 50. Si y = Ae -kt cos(pt + c), demuestre que (d 2 y/dt 2 ) + 2k(dy/dt) + n 2 y = 0, donde n 2 = p 2 + k 2
Solución:
Tenemos,
y = Ae -kt cos(pt + c)
yo,
(dy/dt) = -kAe -kt cos(pt + c) – pAe -kt sin(pt + c)
(dy/dt) = -ky – pAe -kt sin(pt + c)
(d 2 y/dt 2 ) = -k(dy/dt) + pAke -kt sin(pt + c) – p 2 Ake -kt cos(pt + c)
(d 2 y/dt 2 ) = -k(dy/dt) + k(-ky – dy/dx) – p 2 y
(d 2 y/dt 2 ) = -k(dy/dt) – k 2 y – k(dy/dt) – p 2 y
(d 2 y/dt 2 ) + 2k(dy/dt) + (k 2 + p 2 )y = 0
(d 2 y/dt 2 ) + 2k(dy/dt) + n 2 y = 0
Por lo tanto probado
Pregunta 51. Si y = x n {acos(logx) + bsin(logx)}, demuestre que x 2 (d 2 y/dt 2 ) + (1 – 2n) x (dy/dt) + (1 + n 2 )y = 0.
Solución:
Tenemos,
y = x n {acos(logx) + bsen(logx)} …(i)
(dy/dx) = nx n-1 {acos(logx) + bsin(logx)} + x n {-asin(logx).(1/x) + bcos(logx).(1/x)}
x(dy/dx) = nx n {acos(logx) + bsen(logx)} + x n {-asin(logx) + bcos(logx)}
x(dy/dx) = ny + x n {-asin(logx) + bcos(logx)} …(ii)
x norte {-asin(logx) + bcos(logx)} = x(dy/dx) – ny …(iii)
x(d 2 y/dx 2 ) + (dy/dx) = n(dy/dx) + nx n-1 {-asin(logx) + bcos(logx)} + x n {-acos(logx).( 1/x) – bsen(logx).(1/x)}
x 2 (d 2 y/dx 2 ) + (dy/dx) = nx(dy/dx) + nx n {-asin(logx) + bcos(logx)} – x n {acos(logx) + bsin(logx )}
x 2 (d 2 y/dx 2 ) = n x (dy/dx) + n{x(dy/dx) – ny} – y – (dy/dx) [De la ecuación (ii) y (iii)]
x 2 (d 2 y/dx 2 ) = nx(dy/dx) + nx(dy/dx) – (dy/dx) – n 2 y – y
x 2 (d 2 y/dx 2 ) = (dy/dx) x [2n – 1] – (n 2 + 1)y
x 2 (d 2 y/dt 2 ) + (1 – 2n) x (dy/dt) + (1 + n 2 )y = 0
Por lo tanto probado
Pregunta 52. y = ![Rendered by QuickLaTeX.com a[x + \sqrt{x^2+1}]^n+b[x - \sqrt{x^2+1}]^{-n}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7b86897c2393a9cb4ea191c17266fd10_l3.png) , demuestre que (x 2 +1)d 2 y/d 2 x + xdy/dx – ny = 0.
, demuestre que (x 2 +1)d 2 y/d 2 x + xdy/dx – ny = 0.
Solución:
tenemos y =
d 2 y/dx 2 =
d 2 y/dx 2 =
d 2 y/dx 2 =
(x 2 +1)d 2 y/d 2 x =
Ahora pon todos estos valores en esta ecuación
(x 2 +1)d 2 y/d 2 x + xdy/dx – ny
Por lo tanto probado
Publicación traducida automáticamente
Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
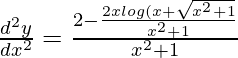

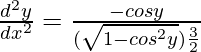
![Rendered by QuickLaTeX.com \frac{nx}{\sqrt{x^2+1}}\frac{dy}{dx}+y[\frac{\sqrt{x^2+1}-x^2(x^2+1)^{-\frac{1}{2}}}{x^2+1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-311e619691976336040e009d17765188_l3.png)