Encuentre la derivada de segundo orden de la siguiente función
Pregunta 1(i). x 3 + tangente
Solución:
Consideremos
f(x) = x3 + tanx
Al diferenciar ambos lados de x,
f'(x) = 3x 2 + seg 2 x
Nuevamente diferenciando ambos lados con x,
f”(x) = 6x + 2(segx)(segx.tanx)
f”(x) = 6x + 2seg 2 x.tanx
Pregunta 1(ii). pecado(logx)
Solución:
Consideremos
y = sen(logx)
Al diferenciar ambos lados de x,
(dy/dx) = cos(logx) × (1/x)
(dy/dx) = cos(logx)/x
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = d/dx[cos(logx)/x]
=
= -[sen(logx) + cos(logx)]/x 2
Pregunta 1(iii). registro (senx)
Solución:
Consideremos
y = log(senx)
Al diferenciar ambos lados de x,
(dy/dx) = (1/senx) × (cosx)
(dy/dx) = cox
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = -coseg 2 x
Pregunta 1(iv). e x sen5x
Solución:
Consideremos
y = e x sen5x
Al diferenciar ambos lados de x,
(dy/dx) = e x sen5x + 5e x cos5x
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = e x sen5x + 5e x cos5x + 5(e x cos5x – 5e x sen5x)
d 2 y/dx 2 = -24e x sen5x + 10e x cos5x
d 2 y/dx 2 = 2e x (5cos5x – 12senx)
Pregunta 1(v). e 6x cos3x
Solución:
Consideremos
y = e 6x cos3x
Al diferenciar ambos lados de x,
(dy/dx) = 6e 6x cos3x – 3e 6x sen3x
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = 6(6e 6x cos3x – 3e 6x sen3x) – 3(6e 6x sen3x + 3e 6x cos3x)
d 2 y/dx 2 = 36e 6x cos3x – 18e 6x sen3x – 18e 6x sen3x – 9e 6x cos3x
d 2 y/dx 2 = 27e 6x cos3x – 36e 6x sen3x
d 2 y/dx 2 = 9e 6x (3 cos 3x – 4 sen 3x)
Pregunta 1 (vi). x 3 logx
Solución:
Consideremos
y = x 3 logx
Al diferenciar ambos lados de x,
(dy/dx) = logx.3x 2 + x 3 (1/x)
(dy/dx) = logx.3x 2 + x 2
(dy/dx) = x 2 (1 + 3logx)
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = (1 + 3logx).2x + x 2 (3/x)
d 2 y/dx 2 = 2x + 6xlogx + 3x
d 2 y/dx 2 = x(5 + 6logx)
Pregunta 1 (vii). bronceado -1x _
Solución:
Consideremos
y = bronceado -1 x
Al diferenciar ambos lados de x,
(dy/dx) = 1/(1 + x 2 )
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = (-1)(1 + x 2 ) -2 .2x
Pregunta 1 (viii). x.cosx
Solución:
Consideremos
y = x.cosx
Al diferenciar ambos lados de x,
(dy/dx) = cosx + x(-senx)
(dy/dx) = cosx – xsenx
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = -senx – (senx + xcosx)
d 2 y/dx 2 = -2senx – xcosx
d 2 y/dx 2 = -(xcosx + 2senx)
Pregunta 1(ix). registro(logx)
Solución:
Consideremos
y = log(logx)
Al diferenciar ambos lados de x,
(dy/dx) = (1/logx) × (1/x)
(dy/dx) = 1/xlogx
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = (-1)(xlogx) -2 .[(d/dx)xlogx]
d 2 y/dx 2 = (-1)(xlogx) -2 [logx+x.(1/x)]
d 2 y/dx 2 = (-1)(xlogx) -2 .(logx+1)
Pregunta 2. Si y = e -x .cosx, demuestre que d 2 y/dx 2 = 2e -x .senx.
Solución:
Consideremos
y = e -x .cosx
Al diferenciar ambos lados de x,
(dy/dx) = -e -x .cosx – e -x .senx
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = -(-e -x .cosx – e -x .senx) – (-e -x .senx + e -x .cosx)
d 2 y/dx 2 = e -x .cosx – e -x .cosx + e -x .sinx + e -x .senx
d 2 y/dx 2 = 2e -x. senx
Por lo tanto probado
Pregunta 3. Si y = x + tanx, demuestre que cos 2 x(d 2 y/dx 2 ) – 2y + 2x = 0.
Solución:
Consideremos
y = x + tanx
Al diferenciar ambos lados de x,
(dy/dx) = 1 + seg 2 x
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = 0 + (2segx)(segx.tanx)
d 2 y/dx 2 = 2 seg 2 x.tanx
Al multiplicar a ambos lados por cos 2 x
cos 2 x(d 2 y/dx 2 ) = 2tanx
cos 2 x(d 2 y/dx 2 ) = 2(y – x) [ya que, tanx = y – x]
cos 2 x(d 2 y/dx 2 ) – 2y + 2x = 0
Por lo tanto probado
Pregunta 4. Si y = x 3 logx, demuestre que (d 4 y/dx 4 ) = (6/x).
Solución:
Consideremos
y = x 3 logx
Al diferenciar ambos lados de x,
(dy/dx) = logx.3x 2 + x 3 (1/x)
(dy/dx) = logx.3x 2 + x 2
(dy/dx) = x 2 (1 + 3logx)
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = (1 + 3logx).2x + x 2 (3/x)
d 2 y/dx2 = 2x + 6xlogx + 3x
d 2 y/dx 2 = 5x + 6xlogx
Nuevamente diferenciando ambos lados con x,
d 3 y/dx 3 = 5 + 6[logx + (x/x)]
d 3 y/dx 3 = 11 + 6logx
Nuevamente diferenciando ambos lados con x,
d 4 y/dx 4 = (6/x)
Por lo tanto probado
Pregunta 5. Si y = log(senx), prueba que (d 3 y/dx 3 ) = 2cosx.cosec 3 x.
Solución:
Let us considered
y = log(sinx)
On differentiating both sides w.r.t x,
(dy/dx) = (1/sinx) × (cosx)
(dy/dx) = cotx
Again differentiating both sides w.r.t x,
d2y/dx2 = -cosec2x
Again differentiating both sides w.r.t x,
d 3 y/dx 3 = -2cosecx.(-cosesx.cotx)
d 3 y/dx 3 = 2cosec 2 x.cotx
d 3 y/dx 3 = 2cosec 2 x.(cosx/senx)
d 3 y/dx 3 = cosx.cosec 3 x
Por lo tanto probado
Pregunta 6. Si y = 2senx + 3cosx, demuestre que (d 2 y/dx 2 ) + y = 0.
Solución:
Consideremos
y = 2senx + 3cosx
Al diferenciar ambos lados de x,
(dy/dx) = 2cosx – 3senx
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = -2senx – 3cosx
d 2 y/dx 2 = -(2senx + 3cosx)
d 2 y/dx 2 = -y
re 2 y/dx 2 + y = 0
Por lo tanto probado
Pregunta 7. Si y = (logx/x), demuestre que (d 2 y/dx 2 ) = (2logx – 3)/x 3
Solución:
Consideremos
y = (logx/x)
Al diferenciar ambos lados de x,
(dy/dx) = (1 – logx)/x 2
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = [-x – 2x(1 – logx)]/x 4
d 2 y/dx 2 = (2xlogx – 3x)/x 4
d 2 y/dx 2 = (2logx – 3)/x 3
d2y/dx2 + y = 0
Por lo tanto probado
Pregunta 8. Si x = a secθ, y = b tanθ, demuestre que (d 2 y/dx 2 ) = -b 4 /a 2 y 3
Solución:
Tenemos,
x = a secθ y y = b tanθ
Al diferenciar ambos lados con θ,
(dx/dθ) = a secθ.tanθ, (dy/dθ) = b sec 2 θ
(dy/dx) = (dy/dθ) × (dθ/dx)
(dy/dx) = (b sec 2 θ)/(a secθ.tanθ)
(dy/dx) = (b/a).cosecθ
Nuevamente diferenciando ambos lados con x,
(d 2 y/dx 2 ) = (b/a).(-cosecθ.cotθ).(dθ/dx)
(d 2 y/dx 2 ) = -(b/a).(cosecθ.cotθ).(1/a secθ.tanθ)
(d 2 y/dx 2 ) = – (b/a 2 ).(cotθ).(1/tan 2 θ)
d 2 y/dx 2 = -(b/a 2 ).(1/tan 3 θ)
d 2 y/dx 2 = -(b/a 2 tan 3 θ).(b 3 /b 3 )
d 2 y/dx 2 = -(b 4 /a 2 y 3 )
Por lo tanto probado
Pregunta 9. Si x = a(cost + tsint) y y = a(sint – tcost), demuestre que d 2 y/dx 2 = sec 3 t/ at 0 < t <
Solución:
Tenemos,
x = a(coste + tsint) y y=a(sint – tcoste)
Al diferenciar ambos lados wrt t,
(dx/dt) = a(-sint + sint + tcoste), (dy/dt) = a(coste – coste + tsint)
(dx/dt) = al costo, (dy/dt) = al costo
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = atsint × [1/atcost]
(dy/dx) = cantidad
Nuevamente diferenciando ambos lados con x,
(d 2 y/dx 2 ) = seg 2 x.(dt/dx)
(d 2 y/dx 2 ) = sec2x.[1/a costo]
(d 2 y/dx 2 ) = seg 3 x/en
Por lo tanto probado
Pregunta 10. Si y = e x cosx, demuestre que d 2 y/dx 2 = 2e x cos(x + π/2).
Solución:
Tenemos,
y = e x cos x
Al diferenciar ambos lados de x,
(dy/dx) = e x cosx – e x senx
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = (e x cosx – e x senx) – (e x senx + e x cosx)
d 2 y/dx 2 = e x cosx – e x cosx – e x senx – e x senx
d 2 y/dx 2 = -2e x senx
d 2 y/dx 2 = 2e x cos(x + π/2)
Pregunta 11. Si x = a cosθ, y = b sinθ, demuestre que (d 2 y/dx 2 ) = -b 4 /a 2 y 3
Solución:
Tenemos,
x = a cosθ y y = b sinθ
Al diferenciar ambos lados con θ,
(dx/dθ) = -a sinθ, (dy/dθ) = b cosθ
(dy/dx) = (dy/dθ)×(dθ/dx)
(dy/dx) = (b cosθ)/(-a senθ)
(dy/dx) = -(b/a).cotθ
Nuevamente diferenciando ambos lados con x,
(d 2 y/dx 2 ) = -(b/a).(-cosec 2 θ).(dθ/dx)
(d 2 y/dx 2 ) = (b/a).(cosec 2 θ).(1/-a senθ)
(d 2 y/dx 2 ) = (b/a).(cosec 2 θ).(1/-a senθ)
d 2 y/dx 2 = -(b/a 2 ).(1/sen 3 θ)
d 2 y/dx 2 =-(b/a 2 sen 3 θ).(b 3 /b 3 )
d 2 y/dx2 = -(b 4 /a 2 y 3 ) (ya que y = a senθ)
Por lo tanto probado
Pregunta 12. Si x = a(1 – cos 3 θ), y = a sen 3 θ, demuestre que (d 2 y/dx 2 ) = 32/27a, en θ = π/6.
Solución:
Tenemos,
x = a(1 – cos 3 θ) y y = a sen 3 θ
Al diferenciar ambos lados con θ,
(dx/dθ) = a(3cos 2 θ.senθ), (dy/dθ) = a 3sen 2 θcosθ
(dx/dθ) = 3acos 2 θ.senθ, (dy/dθ) = 3asen 2 θ.cosθ
(dy/dx) = (dy/dθ) × (dθ/dx)
(dy/dx) = (3asen 2 θ.cosθ) × (3acos 2 θ.senθ)
(dy/dx) = tan 2 θ/ tan θ
(dy/dx) = tanθ
Nuevamente diferenciando ambos lados con x,
(d 2 y/dx 2 ) = sec 2 θ(dθ/dx)
(d 2 y/dx 2 ) = sec 2 θ.[1/3acos 2 θ.senθ]
(d 2 y/dx 2 ) = sec 4 θ/3asinθ
En θ = π/6
d 2 y/dx 2 = seg 4 (π/6)/3asin(π/6)
d 2 y/dx 2 = 32/27a
Por lo tanto probado
Pregunta 13. Si x = a(θ + senθ), y = a(1 + cosθ), demuestre que (d 2 y/dx 2 ) = -(a/y 2 ).
Solución:
Tenemos,
x = a(θ + senθ) y y = a(1 + cosθ)
Al diferenciar ambos lados con θ,
(dx/dθ) = a(1 + cosθ), (dy/dθ) = -asinθ
(dy/dx) = (dy/dθ) × (dθ/dx)
(dy/dx) = [-asinθ] × [a(1 + cosθ)]
(dy/dx) = -sinθ/(1 + cosθ)
Again differentiating both sides w.r.t x,
(d2y/dx2) = -(1 + cosθ)/a(1 + cosθ)3
(d2y/dx2) = -1/a(1 + cosθ)2
(d2y/dx2) = -[1/a(1 + cosθ)2](a/a)
d2y/dx2 = -a/y2
Hence Proved
Pregunta 14. Si x = a(θ – senθ), y = a(1 + cosθ), hallar (d 2 y/dx 2 ).
Solución:
Tenemos,
x = a(θ – senθ) y y = a(1 + cosθ)
Al diferenciar ambos lados con θ,
(dx/dθ) = a(1 – cosθ), (dy/dθ) = -asinθ
(dy/dx) = (dy/dθ) × (dθ/dx)
(dy/dx) = [-asinθ] × [a(1 – cosθ)]
(dy/dx) = -sinθ/(1 – cosθ)
Nuevamente diferenciando ambos lados con x,
(d 2 y/dx 2 ) = 1/a(1 – cosθ) 2
d 2 y/dx 2 = (1/4a)[cosec 4 (θ/2)]
Pregunta 15. Si x = a(1 – cosθ), y = a(θ + sinθ), demuestre que (d 2 y/dx 2 ) = -1/a en θ = π/2.
Solución:
Tenemos,
x = a(1 – cosθ) y y = a(θ + senθ)
Al diferenciar ambos lados con θ,
(dx/dθ) = a(sinθ), (dy/dθ) = a(1 + cosθ)
(dy/dx) = (dy/dθ) × (dθ/dx)
(dy/dx) = [a(1 + cosθ)] × [asinθ)]
(dy/dx) = (1 + cosθ)/senθ
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = (-sen 2 θ – cos θ – cos 2 θ)/asen 3 θ
d 2 y/dx 2 = -(sen 2 θ + cos θ + cos 2 θ)/asen 3 θ
En θ = π/2,
d 2 y/dx 2 = -(1 + 0)/a
d 2 y/dx 2 = -(1/a)
Por lo tanto probado
Pregunta 16. Si x = a(1 + cosθ), y = a(θ + sinθ), demuestre que (d 2 y/dx 2 ) = -1/a en θ = π/2.
Solución:
Tenemos,
x = a(1 + cosθ) y y = a(θ + senθ)
Al diferenciar ambos lados con θ,
(dx/dθ) = a(-sinθ), (dy/dθ) = a(1 + cosθ)
(dy/dx) = (dy/dθ) × (dθ/dx)
(dy/dx) = [a(1 + cosθ)] × [-asinθ)]
(dy/dx) = -(1 + cosθ)/senθ
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = (-sen 2 θ – cos θ – cos 2 θ)/asen 3 θ
d 2 y/dx 2 = -(sen 2 θ + cos θ + cos 2 θ)/asen 3 θ
En θ = π/2,
d 2 y/dx 2 = -(1 + 0)/a
d 2 y/dx 2 = -(1/a)
Por lo tanto probado
Pregunta 17. Si x = cosθ, y = sen 3 θ, demuestre que y(d 2 y/dx 2 ) + (dy/dx) 2 = 3sen 2 θ(5cos 2 θ – 1).
Solución:
Tenemos,
x = cosθ y y = sen 3 θ
Al diferenciar ambos lados con θ,
(dx/dθ) = -sinθ, (dy/dθ) = 3sen 2 θ.cosθ
(dy/dx) = (dy/dθ) × (dθ/dx)
(dy/dx) = [ 3sen 2 θ.cosθ] × [-senθ]
(dy/dx) = -3sinθ.cosθ
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = -3[sinθ(-sinθ) + cosθ.cosθ](dθ/dx)
d 2 y/dx 2 = (3sen 2 θ – 3cos 2 θ)/-senθ
d 2 y/dx 2 = -(3sen 2 θ – 3cos 2 θ)/senθ
LHS,
y(d 2 y/dx 2 ) + (dy/dx) 2 = -sen 3 θ[(3sen 2 θ – 3cos 2 θ)/senθ] + (-3senθ.cosθ) 2
= 3sen 2 θ.cos 2 θ – 3sen 4 θ + 9sen 2 θ.cos 2 θ
= 12sen 2 θ.cos 2 θ – 3sen 4 θ
= 3sen 2 θ(4cos 2 θ – sen 2 θ)
= 3sen 2 θ(4cos 2 θ – sen 2 θ – cos 2 θ + cos 2 θ)
= 3sen 2 θ[5cos 2 θ – (sen 2 θ + cos 2 θ)]
= 3sen 2 θ(5cos 2 θ – 1)
= lado derecho
LHS = RHS
Por lo tanto probado
Pregunta 18. Si y = sin(sinx), prueba que (d 2 y/dx 2 ) + tanx.(dy/dx) + ycos 2 x = 0
Solución:
Tenemos,
y = sin(senx)
Al diferenciar ambos lados de x,
(dy/dx) = cos(senx).cosx
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = -sen(senx).cosx.cosx – cos(senx).senx
d 2 y/dx 2 = -sen(senx).cos 2 x – cos(senx).senx
d 2 y/dx 2 = -sen(senx).cos 2 x – cos(senx).cosx.tanx
d 2 y/dx 2 = -y cos 2 x – (dy/dx)tanx
d 2 y/dx 2 + ycos 2 x + (dy/dx)tanx = 0
Por lo tanto probado
Pregunta 19. Si x = sen t, y = sen pt, demuestre que (1 – x 2 )(d 2 y/dx 2 ) – x.(dy/dx) + p 2 y = 0
Solución:
Tenemos,
x = sen t, y y = sen pt
Al diferenciar ambos lados wrt t,
(dx/dt) = cos t, (dy/dt) = pcos pt
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = pcos pt×[1/cos t]
(dy/dx) = pcos pt/cos t
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = (-p 2 sen pt.cos t + pcos pt.sen t)/cos 3 t
d 2 y/dx 2 = -(p 2 sen pt)/cos 2 t + (pcos pt.sen t)/cos 3 t
cos 2 t(d 2 y/dx 2 ) = -p 2 y + x(dy/dx)
(1 – sen 2 x)(d 2 y/dx 2 ) + p 2 y – x(dy/dx) = 0
(1 – y 2 )(d 2 y/dx 2 ) + p 2 y – x(dy/dx) = 0
Pregunta 20. Si y = (sin -1 x) 2 , demuestre que (1 – x 2 )(d 2 y/dx 2 ) – x.(dy/dx) + p 2 y = 0.
Solución:
Tenemos,
y = (sen -1 x) 2 ,
Al diferenciar ambos lados wrt t,
Nuevamente diferenciando ambos lados con x,
d 2 y/dx 2 = [x/(1 – x 2 )](dy/dx) + 2/(1 – x 2 )
(1 – x 2 )d 2 y/dx 2 = x(dy/dx) + 2
(1 – x 2 )d 2 y/dx 2 – x(dy/dx) – 2 = 0
Por lo tanto probado
Pregunta 21. Si y = 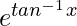 , demuestre que (1 + x 2 )y 2 + (2x – 1)y 1 = 0.
, demuestre que (1 + x 2 )y 2 + (2x – 1)y 1 = 0.
Solución:
Tenemos,
y =
Al diferenciar ambos lados wrt t,
y 1 =
× [1/(1 + x 2 )]
Nuevamente diferenciando ambos lados con x,
y 2 =
(1 + x 2 )y 2 =
/(1 + x 2 ) – 2x
/(1 + x 2 )
(1 + x 2 )y 2 = (dy/dx) – 2x(dy/dx)
(1 + x 2 )y 2 – (dy/dx) + 2x(dy/dx) = 0
(1 + x 2 )y 2 + (2x – 1)(dy/dx) = 0
Por lo tanto probado
Pregunta 22. Si y = 3cos(logx) + 4sin(logx), demuestre que x 2 y 2 + xy 1 + y = 0.
Solución:
Tenemos,
y = 3cos(logx) + 4sen(logx)
Al diferenciar ambos lados de x,
y 1 = -3sen(logx) × (1/x) + 4cos(logx) × (1/x)
xy 1 = -3sen(logx) + 4cos(logx)
Nuevamente diferenciando ambos lados con x,
xy 2 + y 1 = -3cos(logx)×(1/x) – 4sen(logx) × (1/x)
x 2 y 2 + xy 1 = -[3cos(logx) + 4sen(logx)]
x 2 y 2 + xy 1 = -y
x 2 y 2 + xy 1 + y = 0
Por lo tanto probado
Pregunta 23. Si y = e 2x (ax + b), demuestre que y 2 – 4y 1 + 4y = 0.
Solución:
Tenemos,
y = e 2x (ax + b)
Al diferenciar ambos lados con θ,
y 1 = 2e 2x (ax + b) + ae 2x
Nuevamente diferenciando ambos lados con x,
y 2 = 4e 2x (ax + b) + 2ae 2x + 2a.e 2x
y 2 = 4e 2x (ax + b) + 4a.e 2x
Tomemos LH,S,
= y 2 – 4y 1 + 4y
= 4e 2x (ax + b) + 4a.e 2x – 4[2e 2x (ax + b) + ae 2x ] + 4[e 2x (ax + b)]
= 8e 2x (ax + b) – 8e 2x (ax + b) + 4a.e 2x – 4a.e 2x
= 0
= lado derecho
LHS = RHS
Por lo tanto probado
Pregunta 24. Si x = sen(logía/a), demuestre que (1 – x 2 )y 2 – xy 1 – a 2 y = 0.
Solución:
Tenemos,
x = sin(logía/a)
(logía/a) = sen -1 x
logía = asen -1 x
Al diferenciar ambos lados de x,
(1/y)y 1 = a/√(1 – x 2 )
y1 = ay/√(1 – x2 )
Nuevamente diferenciando ambos lados con x,
2 años
(1 – x 2 )y 2 = a√(1 – x 2 ) × y 1 + axy/√(1 – x 2 )
(1 – x 2 )y 2 = a√(1 – x 2 ) × [ay/√(1 – x 2 )] + x[ay/√(1 – x 2 )]
(1 – x 2 )y 2 = a 2 p + xy
(1 – x 2 )y 2 – a 2 p – xy 1 = 0
Por lo tanto probado
Pregunta 25. Si logy = tan -1 x, demuestre que (1 + x 2 )y 2 + (2x – 1)y 1 = 0.
Solución:
Tenemos,
logía = tan -1 x
Al diferenciar ambos lados con θ,
(1/y)y 1 = 1/(1 + x 2 )
(1 + x 2 ) y 1 = y
Nuevamente diferenciando ambos lados con x,
2xy 1 + (1 + x 2 ) y 2 = y 1
(1 + x 2 )y 2 + (2x – 1)y 1 = 0
Por lo tanto probado
Pregunta 26. Si y = tan -1 x, demuestre que (1 + x 2 )(d 2 y/dx 2 ) + 2x(dy/dx) = 0.
Solución:
Tenemos,
y = bronceado -1 x
Al diferenciar ambos lados de x,
(dy/dx) = 1/(1 + x 2 )
Nuevamente diferenciando ambos lados con x,
re 2 y/dx 2 = [-1/(1 + x 2 ) 2 ] × (2x)
re 2 y/dx 2 = [-2x/(1 + x 2 ) 2 ]
(1 + x 2 )(d 2 y/dx 2 ) = -2x/(1 + x 2 )
(1 + x 2 )(d 2 y/dx 2 ) = -2x(dy/dx)
(1 + x 2 )(d 2 y/dx 2 ) + 2x(dy/dx) = 0
Por lo tanto probado
Publicación traducida automáticamente
Artículo escrito por vivekray59 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
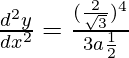
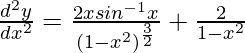
![Procesado por QuickLaTeX.com =a[\frac{\sqrt{1-x^2}\frac{dy}{dx}-\frac{2xy}{2\sqrt{1-x^2}}}{1-x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc1c1c4bddd55c24d0c05037a708a3fc_l3.png)