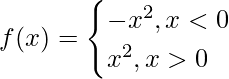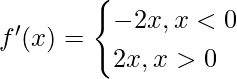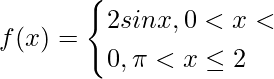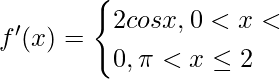Pregunta 26. Encuentra los intervalos en los que f(x) = log (1 + x) – x/(1 + x) es creciente o decreciente.
Solución:
Tenemos,
f(x) = registro (1 + x) – x/(1 + x)
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) =
f'(x) =
f'(x) =
f'(x) =
f'(x) =
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=>
= 0
=> x = 0
Claramente, f'(x) > 0 si x > 0.
Además, f'(x) < 0 si –1 < x < 0 o x < –1.
Así f(x) es creciente en (0, ∞) y decreciente en (–∞, –1) ∪ (–1, 0).
Pregunta 27. Encuentra los intervalos en los que f(x) = (x + 2)e –x es creciente o decreciente.
Solución:
Tenemos,
f(x) = (x + 2)e –x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = e –x – e –x (x + 2)
f'(x) = e –x (1 – x – 2)
f'(x) = e –x (x + 1)
Para f(x), necesitamos encontrar el punto crítico, así que obtenemos,
=> f'(x) = 0
=> e –x (x + 1) = 0
=> x = –1
Claramente, f'(x) > 0 si x < –1.
Además, f'(x) < 0 si x > –1.
Así f(x) es creciente en (–∞, –1) y decreciente en (–1, ∞).
Pregunta 28. Demuestra que la función f dada por f(x) = 10 x es creciente para todo x.
Solución:
Tenemos,
f(x) = 10x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 10 x log 10
Ahora tenemos, x ∈ R, obtenemos
=> 10 x > 0
=> 10 x registro 10 > 0
=> f'(x) > 0
Por tanto, f(x) es creciente para todo x.
Por lo tanto probado.
Pregunta 29. Demuestra que la función f dada por f(x) = x – [x] es creciente en (0, 1).
Solución:
Tenemos,
f(x) = x – [x]
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 1
Ahora tenemos,
=> 1 > 0
=> f'(x) > 0
Así, f(x) es creciente en el intervalo (0, 1).
Por lo tanto probado.
Pregunta 30. Demuestra que la función f(x) = 3x 5 + 40x 3 + 240x es creciente en R.
Solución:
Tenemos,
f(x) = 3x 5 + 40x 3 + 240x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 15x 4 + 120x 2 + 240
f'(x) = 15 (x 4 + 8x 2 + 16)
f'(x) = 15 (x 2 + 4) 2
Ahora sabemos,
=> (x 2 + 4) 2 > 0
=> 15 (x 2 + 4) 2 > 0
=> f'(x) > 0
Por lo tanto, la f(x) dada es creciente en R.
Por lo tanto probado.
Pregunta 31. Demostrar que la función f dada por f(x) = log cos x es estrictamente creciente en (–π/2, 0) y estrictamente decreciente en (0, π/2).
Solución:
Tenemos,
f(x) = logaritmo cos x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) =
f'(x) =
f'(x) = – tan x
Ahora para x ∈ (0, π/2), obtenemos
=> 0 <x <π/2
=> bronceado 0 < bronceado x < bronceado π/2
=> 0 < tan x < 1
=> tan x > 0
=> – tan x < 0
=> f'(x) < 0
También para x ∈ (–π/2, 0), tenemos,
=> –π/2 < x < 0
=> bronceado (–π/2) < bronceado x < bronceado 0
=> –1 < tan x < 0
=> tan x < 0
=> – tan x > 0
=> f'(x) > 0
Así, f(x) es estrictamente creciente en el intervalo (–π/2, 0) y estrictamente decreciente en el intervalo (0, π/2).
Por lo tanto probado.
Pregunta 32. Muestre que la función f dada por f(x) = x 3 – 3x 2 + 4x es estrictamente creciente en R.
Solución:
Tenemos,
f(x) = x 3 – 3x 2 + 4x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 3x 2 – 6x + 4
f'(x) = 3 (x 2 – 2x + 1) + 1
f'(x) = 3 (x – 1) 2 + 1
Ahora sabemos,
=> (x – 1) 2 > 0
=> 3 (x – 1) 2 > 0
=> 3 (x – 1) 2 + 1 > 0
=> f'(x) > 0
Por tanto, f(x) es estrictamente creciente en R.
Por lo tanto probado.
Pregunta 33. Demostrar que la función f dada por f(x) = cos x es estrictamente decreciente en (0, π), creciente en (π, 2π) y ni creciente ni decreciente en (0, 2π).
Solución:
Tenemos,
f(x) = cos x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = – sen x
Ahora para x ∈ (0, π), obtenemos
=> 0 <x <π
=> sen 0 < sen x < sen π
=> 0 < sen x < 0
=> sen x > 0
=> – sen x < 0
=> f'(x) < 0
También para x ∈ (π, 2π), obtenemos
=> π < x < 2π
=> sen 0 < sen x < sen π
=> 0 < sen x < 0
=> sen x < 0
=> – sen x > 0
=> f'(x) > 0
Así, f(x) es estrictamente creciente en el intervalo (π, 2π) y estrictamente decreciente en el intervalo (0, π).
Entonces, la función no es ni creciente ni decreciente en (0, 2π).
Por lo tanto probado.
Pregunta 34. Muestre que f(x) = x 2 – x sen x es una función creciente en (0, π/2).
Solución:
Tenemos,
f(x) = x 2 – x sen x
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 2x – (x cos x + sen x)
f'(x) = 2x – x cos x – sen x
Ahora para x ∈ (0, π/2), tenemos
=> 0 ≤ sen x ≤ 1
=> 0 ≤ porque x ≤ 1
Entonces, esto implica,
=> 2x – x cos x – sen x > 0
=> f'(x) > 0
Así, f(x) es una función creciente en el intervalo (0, π/2).
Por lo tanto probado.
Pregunta 35. Encuentra el(los) valor(es) de a para el cual f(x) = x 3 – ax es una función creciente en R.
Solución:
Tenemos,
f(x) = x 3 – hacha
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 3x 2 – a
Ahora sabemos que f(x) = x 3 – ax es una función creciente en R, obtenemos
=> f'(x) > 0
=> 3x 2 – a > 0
=> un < 3x 2
El punto crítico para 3x 2 = 0 será 0.
Entonces, obtenemos un ≤ 0.
Por lo tanto, los valores de a deben ser menores o iguales a 0.
Pregunta 36. Encuentra el valor de b para el cual la función f(x) = sen x – bx + c es una función decreciente en R.
Solución:
Tenemos,
f(x) = sen x – bx + c
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = cos x – b + 0
f'(x) = cos x – b
Ahora sabemos que f(x) = sen x – bx + c es una función decreciente en R, obtenemos
=> f'(x) < 0
=> cos x – b < 0
=> b > cos x
El punto crítico para cos x = 0 será 1.
Entonces, obtenemos b ≥ 1.
Por lo tanto, los valores de b deben ser mayores o iguales a 1.
Pregunta 37. Muestre que f(x) = x + cos x – a es una función creciente en R para todos los valores de a.
Solución:
Tenemos,
f(x) = x + cos x – a
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) = 1 – sen x
f'(x) =
f'(x) =
Ahora para x ∈ R, tenemos
=>
> 0
=> f'(x) > 0
Por lo tanto, f(x) es una función creciente en R para todos los valores de a.
Por lo tanto probado.
Pregunta 38. Sea f definida en [0, 1] dos veces diferenciable tal que |f”(x)| ≤ 1 para todo x ∈ [0, 1]. Si f(0) = f(1), entonces demuestre que f'(x) < 1 para todo x ∈ [0, 1].
Solución:
Como f(0) = f(1) y f es diferenciable, podemos aplicar aquí el teorema de Rolle. Entonces, obtenemos
f(c) = 0 para algún c ∈ [0, 1].
Al aplicar el teorema del valor medio de Lagrange, obtenemos,
Para el punto c y x ∈ [0, 1], entonces tenemos
=>
=>
=>
Como se nos da que |f”(d)| ≤ 1 para x ∈ [0, 1], obtenemos
=>
≤ 1
=> |f'(x)| ≤ x – c
Ahora, como tanto x como c están en [0, 1], entonces x – c ∈ (0, 1).
Esto nos da, |f'(x)| < 1 para todo x ∈ (0, 1).
Por lo tanto probado.
Pregunta 39. Encuentra el intervalo en el que f(x) es creciente o decreciente:
(i) f(x) = x |x|, x ∈ R
Solución:
Tenemos,
f(x) = x |x|, x ∈ R
=>
=>
=> f'(x) > 0 para todos los valores de x
Por lo tanto, f(x) es una función creciente para todos los valores reales.
(ii) f(x) = sen x + |sen x|, 0 < x ≤ 2π
Solución:
Tenemos,
f(x) = sen x + |sen x|, 0 < x ≤ 2π
=>
=>
La función cos x es positiva entre el intervalo (0, π/2).
Por tanto, la función es creciente en el intervalo (0, π/2).
Además, la función cos x es negativa entre el intervalo (π/2, π).
Por tanto, la función es decreciente en el intervalo (0, π/2).
Ahora, para π ≤ x ≤ 2π, el valor de f'(x) es 0.
Por tanto, la función no es ni creciente ni decreciente en el intervalo (π, 2π).
(iii) f(x) = sen x (1 + cos x), 0 < x ≤ π/2
Solución:
Tenemos,
f(x) = sen x (1 + cos x)
Al diferenciar ambos lados con respecto a x, obtenemos
f'(x) =
f'(x) =
f'(x) = –sen 2 x + cos x + cos 2 x
f'(x) = cos 2 x – sen 2 x + cos x
f'(x) = cos 2 x – (1 – cos 2 x) + cos x
f'(x) = cos 2 x – 1 + cos 2 x + cos x
f'(x) = 2 cos 2 x + cos x – 1
f'(x) = 2 cos 2 x + 2 cos x – cos x – 1
f'(x) = 2 cos x (cos x + 1) – 1 (cos x + 1)
f'(x) = (2 cos x – 1) (cos x + 1)
Para que f(x) sea creciente, debemos tener,
=> f'(x) > 0
=> (2 cos x – 1) (cos x + 1) > 0
=> 0 <x <π/3
=> x ∈ (0, π/3)
Para que f(x) sea decreciente, debemos tener,
=> f'(x) < 0
=> (2 cos x – 1) (cos x + 1) > 0
=> π/3 < x < π/2
=> x ∈ (π/3, π/2)
Así, f(x) es creciente en el intervalo x ∈ (0, π/3) y decreciente en el intervalo x ∈ (π/3, π/2).
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA