Clase 8 Soluciones RD Sharma – Capítulo 3 Cuadrados y raíces cuadradas – Ejercicio 3.3 | conjunto 2

Capítulo 3 Cuadrados y Raíces Cuadradas – Ejercicio 3.3 | Serie 1

Pregunta 4. Encuentra los cuadrados de los siguientes números:

(yo) 425

Solución:

425 = 420 + 5 = (42 x 10) + 5

Aquí, n = 42

=> n(n + 1) = 42(42 + 1) = 42 x 43 = 1806

=> 425 ² = 180625

(ii) 575

Solución:

575 = 570 + 5 = (57 x 10) + 5

Aquí, n = 57

=> n(n + 1) = 57(57 + 1) = 57 x 58 = 3306

=> 575 ² = 330625

(iii) 405

Solución:

405 = 400 + 5 = (40×10) + 5

Aquí, n = 40

=> n(n + 1) = 40(40 + 1) = 1640

=> 405 ² = 164025

(iv) 205

Solución:

205 = 200 + 5 = (20 x 10) + 5

Aquí, n = 20

=> n(n + 1) = 20(20 + 1) = 420

=> 205 ² = 42025

(v) 95

Solución:

95 = 90 + 5 = (9 x 10) + 5

Aquí, n = 9

=> n(n + 1) = 9(9 + 1) = 90

=> 95 ² = 9025

(v) 745

Solución:

745 = 740 + 5 = (74 x 10) + 5

Aquí, n = 74

=> n(n+1) = 74(74 + 1) = 5550

=> 745 ² = 555025

(vii) 512

Solución:

512² = (250 + 12)1000 + (12)² 

= (262)1000 + 144

= 262000 + 144

= 262144

Por lo tanto, 512 ² = 262144

(viii) 995

Solución:

995 = 990 + 5 = (99 x 10) + 5

Aquí, n = 99

=>n(n+1) = 99(99 + 1) = 9900

995 ² = 990025

Pregunta 5. Encuentra el cuadrado de los siguientes números usando la fórmula: (a + b) ² = a ² + 2ab + b ²

(yo) 405 

Solución:

405 = 400 + 5 

Aquí, a = 400, b = 5

Usando la identidad, (a + b) ² = a ² + 2ab + b ²

405 ² = 400 ² + (2 x 400 x 5) + 5 ²

= 160000 + 4000 + 25

= 164025

Así, 405 ² = 164025

(ii) 510

Solución:

510 = 500 + 10

Aquí, a = 500, b = 10 

Usando la identidad, (a + b) ² = a ² + 2ab + b ²

510 ² = 500 ² + (2 x 500 x 10) + 10 ²

= 250000 + 10000 + 100

= 260100

Así, 510 ² = 260100

(iii) 1001

Solución:

1001 = 1000 + 1

Aquí, a = 1000, b = 1

Usando la identidad, (a + b) ² = a ² + 2ab + b ²

1001 ² = 1000 ² + (2 x 1000 x 1) + 1 ²

= 1000000 + 2000 + 1

= 1002001

Así, 1001 ² = 1002001 

(iv) 209

Solución:

209 = 200 + 9

Aquí, a = 200, b = 9

Usando la identidad, (a + b) ² = a ² + 2ab + b ²

209 ² = 200 ² + (2 x 200 x 9) + 9 ²

= 40000 + 3600 + 81

= 43681

Por lo tanto, 209 ² = 43681

(vi) 605

Solución:

605 = 600 + 5

Aquí, a = 600, b = 5

Usando la identidad, (a + b) ² = a ² + 2ab + b ² 

605 ² = 600 ² + (2 x 600 x 5) + 5 ²

= 360000 + 6000 + 25

= 366025

Por lo tanto, 605 ² = 366025

Pregunta 6. Encuentra el cuadrado de los siguientes números usando la fórmula: (a – b)² = a² – 2ab + b²

(yo) 395

Solución:

395 = 400 – 5

Aquí, a = 400, b = 5

Usando la identidad, (a – b) ² = a ² – 2ab + b ² 

395 ² = (400 – 5) ² = 400 ² – (2 x 400 x 5) + 5 ²

= 160000 – 4000 + 25

= 156025

Así, 395 ² = 156025

(ii) 995

Solución:

995 = 1000 – 5

Aquí, a = 1000, b = 5

Usando la identidad, (a – b) ² = a ² – 2ab + b ²

995 ² = (1000 – 5) ² = 1000 ² – (2 x 1000 x 5) + 5 ²

= 1000000 – 10000 + 25

= 990025

Así, 995 ² = 990025

(iii) 495

Solución:

495 = 500 – 5

Aquí, a = 500, b = 5

Usando la identidad, (a – b) ² = a ² – 2ab + b ²

495 ² = (500 – 5) ² = 500 ² – (2 x 500 x 5) + 5 ²

= 250000 – 5000 + 25

= 245025

Así, 495 ² = 245025

(iv) 498

Solución:

498 = 500 – 2

Aquí, a = 500, b = 2

Usando la identidad, (a – b) ² = a ² – 2ab + b ²

498 ² = (500 – 2) ² = 500 ² – (2 x 500 x 2) + 2 ²

= 250000 – 2000 + 4

= 248004

Así, 498 ² = 248004

(v) 99

Solución:

99 = 100 – 1

Aquí, a = 100, b = 1

99 ² = (100 – 1) ² = 100 ² – (2 x 100 x 1) + 1 ²

= 10000 – 200 + 1

= 9801

Usando la identidad, (a – b) ² = a ² – 2ab + b ²

Así, 99 ² = 9801

(vi) 999

Solución:

999 = 1000 – 1

Aquí, a = 1000, b = 1

Usando la identidad, (a – b) ² = a ² – 2ab + b ²

999 ² = (1000 – 1) ² = 1000 ² – (2 x 1000 x 1) + 1 ²

= 1000000 – 2000 + 1

= 998001 

Por lo tanto, 999 ² = 998001

(vii) 599

Solución:

599 = 600 – 1

Aquí, a = 600, b = 1

Usando la identidad, (a – b) ² = a ² – 2ab + b ²

599 ² = (600 – 1) ² = 600 ² – (2 x 600 x 1) + 1 ²

= 360000 – 1200 + 1

= 358801

Así, 599 ² = 358801

Pregunta 7. Encuentra los cuadrados de los siguientes números por el método visual:

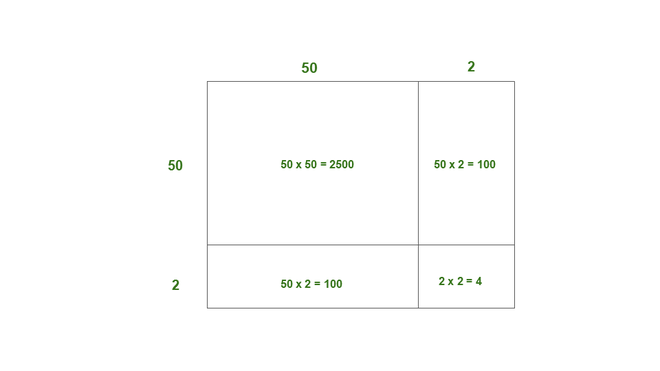
(yo) 52

Solución:

52 = 50 + 2

Aquí, a = 50, b = 2

Así, el área del cuadrado de lado 52 = 2500 + 100 + 100 + 4

= 2704 

Así, 52 ² = 2704

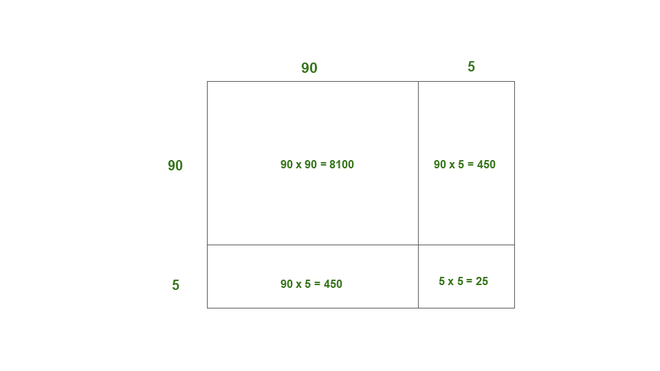
(ii) 95

Solución:

95 = 90 + 5

Aquí, a = 90, b = 5

Así, el área del cuadrado de lado de 95 = 8100 + 450 + 450 + 25

= 9025

Así, 95 ² = 9025

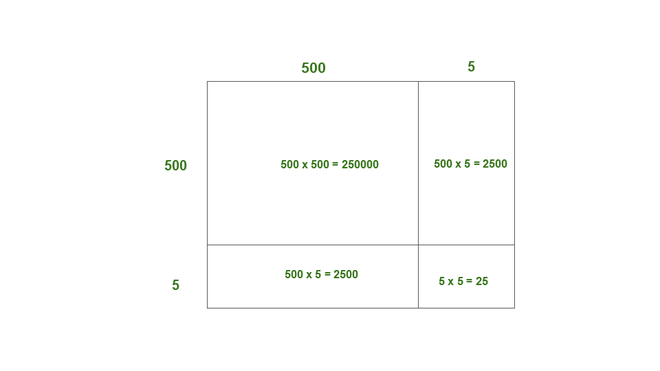
(iii) 505

Solución:

505 = 500 + 5

Aquí, a = 500, b = 5

Así, el área del cuadrado de lado 505 = 250000 + 2500 + 2500 + 25

= 255025

Así, 505 ² = 255025

(iv) 702

Solución:

702 = 700 + 2

Aquí, a = 700, b = 2

Así, el área del cuadrado de lado 702 = 490000 + 1400 + 1400 + 4

= 492804

Así, 702 ² = 492804

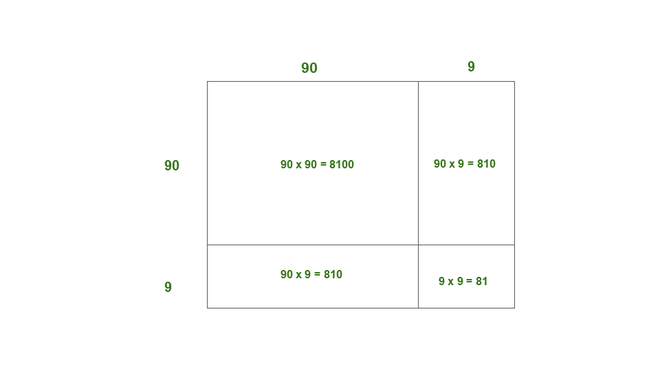
(v) 99

Solución:

99 = 90 + 9

Aquí, a = 90, b = 9.

Así, el área del cuadrado de lado de 99 = 8100 + 810 + 810 + 81

= 9801 

Así, 99 ² = 9801