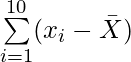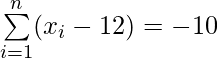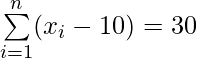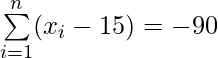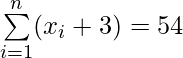Pregunta 13. La policía de tránsito registró la velocidad (en km/h) de 10 automovilistas como 47, 53, 49, 60, 39, 42, 55, 57, 52, 48. Posteriormente se encontró un error en el instrumento de registro. Encuentre la velocidad promedio correcta de los automovilistas si el instrumento registró 5 km/h menos en cada caso.
Solución:
Dado: La velocidad de 10 automovilistas es 47,53,49,60,39,42,55,57,52,48.
Más tarde se descubrió que el instrumento registraba 5 km/h menos que en cada caso
Por lo tanto, los valores correctos son = 52,58,54,65,44,47,60,62,57,53.
Media=(suma de números)/(números totales)
Por lo tanto, media correcta=(52+58+54+65+44+47+60+62+57+53)/(10)
=552/10 = 55,2 km/h
Pregunta 14. La media de cinco números es 27. Si se excluye un número, su media es 25. Encuentra el número excluido.
Solución:
Dado: La media de cinco números es 27
La suma de cinco números = 5 * 27 = 135
Si se excluye un número, la nueva media es 25
Por lo tanto, Suma de 4 números = 4 * 25 = 100
Por lo tanto, Número excluido = 135 – 100 = 35
Pregunta 15. El peso medio por alumno en un grupo de 7 alumnos es de 55 kg. Los pesos individuales de 6 de ellos (en kg) son 52, 54, 55, 53, 56 y 54. Encuentra el peso del séptimo estudiante.
Solución:
Dado: El peso medio por estudiante en un grupo de 7 estudiantes = 55 kg
Peso de 6 alumnos (en kg) = 52,54,55,53,56 y 54
Sea el peso del séptimo estudiante = x kg
Peso medio = (suma de pesos)/(número total de pesos)
55 = (52+54+55+53+56+54+x)/7
385 = 324 + x
x = 385-324
x = 61 kg
Por lo tanto, peso del séptimo estudiante = 61 kg.
Pregunta 16. El peso medio de 8 números es 15. Si cada número se multiplica por 2, ¿cuál será el nuevo medio?
Solución:
Dado: El peso medio de 8 números es 15
Entonces, la suma de 8 números = 8 * 15 = 120
Si cada número se multiplica por 2
Entonces, la nueva suma de 8 números = 120 * 2 = 240
Media=(suma de números)/(números totales)
Por lo tanto, nueva media = 240/8 = 30.
Pregunta 17. La media de 5 números es 18. Si se excluye un número, su media es 16. Encuentra el número excluido.
Solución:
Dado: La media de 5 números es 18
Entonces, la suma de 5 números = 5 * 18 = 90
Si se excluye un número
Entonces, la media de 4 números = 16
Por lo tanto, suma de 4 números = 4 * 16 = 64
Número excluido = 90 – 64 = 26.
Pregunta 18. La media de 200 ítems fue 50. Más tarde, se descubrió que los dos ítems se malinterpretaron como 92 y 8 en lugar de 192 y 88. Encuentra la media correcta.
Solución:
Dado: La media de 200 elementos = 50
Entonces la suma de 200 artículos = 200 * 50 = 10,000
Valores correctos = 192 y 88.
Valores incorrectos = 92 y 8.
Por lo tanto, la suma correcta = 10000 – 92 – 8 + 192 + 88 = 10180
Media=(suma de números)/(números totales)
Por lo tanto, media correcta = 10180/200 = 50,9.
Pregunta 19. Si M es la media de x1, x2, x3, x4, x5 y x6, prueba que
(x1 – M) + (x2 – M) + (x3 – M) + (x4 – M) + (x5 – M) + (x6 – M) = 0.
Solución:
Dado: Sea M la media de x1, x2, x3, x4, x5 y x6
Entonces M= (x1 + x2 + x3 + x4 + x5 + x6)/6
(x1 + x2 + x3 + x4 + x5 + x6)= 6M
Para probar: (x1 – M) + (x2 – M) + (x3 – M) + (x4 – M) + (x5 – M) + (x6 – M) = 0
Prueba:
L .HS = (x1 – M) + (x2 – M) + (x3 – M) + (x4 – M) + (x5 – M) + (x6 – M)
= (x1 + x2, + x3 + x4 + x5 + x6) – (M + M + M + M + M + M)
= 6M – 6M
= 0
= lado derecho
Por lo tanto probado.
Pregunta 20. Las duraciones de la luz solar (en horas) en Amritsar durante los primeros 10 días de agosto de 1997 según lo informado por el Departamento Meteorológico son las siguientes: 9.6, 5.2, 3.5, 1.5, 1.6, 2.4, 2.6, 8.4, 10.3, 10.9
(i) Encuentre la media ![]()
(ii) Verificar que 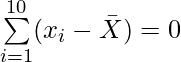
Solución:
La duración de la insolación (en horas) durante 10 días es = 9,6,5,2,3,5,1,5,1,6,2,4,2,6,8,4,10,3,10,9
(i) Media
= (suma de números)/ (números totales)
=(9,6+5,2+3,5+1,5+1,6+2,4+2,6+8,4+10,3+10,9)/10
=56/10=5,6
(II) IZQ =
=
=(9,6 – 5,6) + (5,2 – 5,6) + (3,5 – 5,6) + (1,5 – 5,6) + (1,6 – 5,6) + (2,4 – 5,6) + (2,6 – 5,6) + (8,4 – 5,6) + ( 10.3 – 5.6) + (10.9 – 5.6)
= 4 – 0,4 – 2,1 – 4,1 – 4 – 3,2 – 3 + 2,8 + 4,7 + 5,3
= 16,8-16,8 = 0
= lado derecho
Pregunta 21. Encuentra los valores de n y 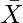 cada uno de los siguientes casos:
cada uno de los siguientes casos:
(yo) 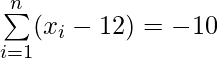 y
y 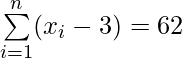
(ii) 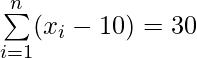 y
y 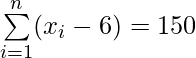
Solución:
(i) Dado:
——— Ecuación 1
y
——— Ecuación 2
Al restar la ecuación 1 de la ecuación 2, obtenemos
Pon el valor de n en la ecuación 1
(ii)
Dado:
——— Ecuación 1
y
——— Ecuación 2
Al restar la ecuación 1 de la ecuación 2, obtenemos
Pon el valor de n en la ecuación 1
Pregunta 22. Las sumas de las desviaciones de un conjunto de n valores x1, x2,… xn medidas a partir de 15 y -3 son -90 y 54 respectivamente. Encuentre el valor de n y la media.
Solución:
Dado:
——— Ecuación 1
y
——— Ecuación 2
Al restar la ecuación 1 de la ecuación 2, obtenemos
Pon el valor de n en la ecuación 1
Pregunta 23. Encuentra la suma de las desviaciones de los valores variables 3, 4, 6, 7, 8, 14 de su media.
Solución:
Dado: Los valores son 3,4,6,7,8,14
Media=(suma de números)/(números totales)
Por lo tanto, Media = (3 + 4 + 6 + 7 + 8 + 14) / 6
Media=42/6=7
Por lo tanto, la suma de la desviación de los valores de su media = (3 – 7) + (4 – 7) + (6 – 7) + (7 – 7) + (8 – 7) + (14 – 7)
= -4-3-1 +0 + 1+7
=-8+8=0
Pregunta 24. Si 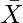 es la media de los diez números naturales,
es la media de los diez números naturales, 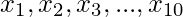 demuestre que
demuestre que 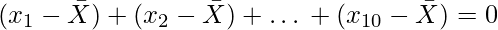
Solución:
Tenemos,
Ahora,
hasta 10 términos)
Publicación traducida automáticamente
Artículo escrito por manandeep1610 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA