En la teoría de grafos, la coloración de los bordes de un gráfico es una asignación de «colores» a los bordes del gráfico para que no haya dos bordes adyacentes que tengan el mismo color con una cantidad óptima de colores. Se dice que dos aristas son adyacentes si están conectadas al mismo vértice. No existe un algoritmo de tiempo polinomial conocido para colorear los bordes de cada gráfico con una cantidad óptima de colores. Sin embargo, se han desarrollado una serie de algoritmos que relajan uno o más de estos criterios, solo funcionan en un subconjunto de gráficos, o no siempre usan una cantidad óptima de colores, o no siempre se ejecutan en tiempo polinomial.
Ejemplos :
Input : u1 = 1, v1 = 4
u2 = 1, v2 = 2
u3 = 2, v3 = 3
u4 = 3, v4 = 4
Output : Edge 1 is of color 1
Edge 2 is of color 2
Edge 3 is of color 1
Edge 4 is of color 2
The above input shows the pair of vertices(ui, vi)
who have an edge between them. The output shows the color
assigned to the respective edges.
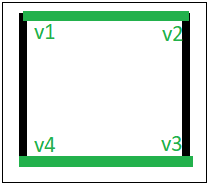
La coloración de bordes es uno de varios tipos diferentes de problemas de coloración de gráficos. La figura anterior de un gráfico muestra la coloración de un borde de un gráfico con los colores verde y negro, en el que ningún borde adyacente tiene el mismo color.
A continuación se muestra un algoritmo para resolver el problema de coloración de bordes que puede no utilizar una cantidad óptima de colores:
Algoritmo:
- Utilice el recorrido BFS para comenzar a recorrer el gráfico.
- Elija cualquier vértice y dé diferentes colores a todos los bordes conectados a él, y marque esos bordes como coloreados.
- Atraviesa uno de sus bordes.
- Repita el paso con un nuevo vértice hasta que todos los bordes estén coloreados.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to illustrate Edge Coloring
#include <bits/stdc++.h>
using namespace std;
// function to determine the edge colors
void colorEdges(int ptr, vector<vector<pair<int, int> > >& gra,
vector<int>& edgeColors, bool isVisited[])
{
queue<int> q;
int c = 0;
unordered_set<int> colored;
// return if isVisited[ptr] is true
if (isVisited[ptr])
return;
// Mark the current node visited
isVisited[ptr] = 1;
// Traverse all edges of current vertex
for (int i = 0; i < gra[ptr].size(); i++) {
// if already colored, insert it into the set
if (edgeColors[gra[ptr][i].second] != -1)
colored.insert(edgeColors[gra[ptr][i].second]);
}
for (int i = 0; i < gra[ptr].size(); i++) {
// if not visited, inset into the queue
if (!isVisited[gra[ptr][i].first])
q.push(gra[ptr][i].first);
if (edgeColors[gra[ptr][i].second] == -1) {
// if col vector -> negative
while (colored.find(c) != colored.end())
// increment the color
c++;
// copy it in the vector
edgeColors[gra[ptr][i].second] = c;
// then add it to the set
colored.insert(c);
c++;
}
}
// while queue's not empty
while (!q.empty()) {
int temp = q.front();
q.pop();
colorEdges(temp, gra, edgeColors, isVisited);
}
return;
}
// Driver Function
int main()
{
set<int> empty;
// declaring vector of vector of pairs, to define Graph
vector<vector<pair<int, int> > > gra;
vector<int> edgeColors;
bool isVisited[100000] = { 0 };
// Enter the Number of Vertices
// and the number of edges
int ver = 4;
int edge = 4;
gra.resize(ver);
edgeColors.resize(edge, -1);
// Enter edge & vertices of edge
// x--; y--;
// Since graph is undirected, push both pairs
// (x, y) and (y, x)
// graph[x].push_back(make_pair(y, i));
// graph[y].push_back(make_pair(x, i));
gra[0].push_back(make_pair(1, 0));
gra[1].push_back(make_pair(0, 0));
gra[1].push_back(make_pair(2, 1));
gra[2].push_back(make_pair(1, 1));
gra[2].push_back(make_pair(3, 2));
gra[3].push_back(make_pair(2, 2));
gra[0].push_back(make_pair(3, 3));
gra[3].push_back(make_pair(0, 3));
colorEdges(0, gra, edgeColors, isVisited);
// printing all the edge colors
for (int i = 0; i < edge; i++)
cout << "Edge " << i + 1 << " is of color "
<< edgeColors[i] + 1 << "\n";
return 0;
}
Python3
# Python3 program to illustrate Edge Coloring
from queue import Queue
# function to determine the edge colors
def colorEdges(ptr, gra, edgeColors, isVisited):
q=Queue()
c = 0
colored=set()
# return if isVisited[ptr] is true
if (isVisited[ptr]):
return
# Mark the current node visited
isVisited[ptr] = True
# Traverse all edges of current vertex
for i in range(len(gra[ptr])) :
# if already colored, insert it into the set
if (edgeColors[gra[ptr][i][1]] != -1):
colored.add(edgeColors[gra[ptr][i][1]])
for i in range(len(gra[ptr])) :
# if not visited, inset into the queue
if not isVisited[gra[ptr][i][0]]:
q.put(gra[ptr][i][0])
if (edgeColors[gra[ptr][i][1]] == -1) :
# if col vector -> negative
while c in colored:
# increment the color
c+=1
# copy it in the vector
edgeColors[gra[ptr][i][1]] = c
# then add it to the set
colored.add(c)
c+=1
# while queue's not empty
while not q.empty() :
temp = q.get()
colorEdges(temp, gra, edgeColors, isVisited)
return
# Driver Function
if __name__=='__main__':
empty=set()
# declaring vector of vector of pairs, to define Graph
gra=[]
edgeColors=[]
isVisited=[False]*100000
# Enter the Number of Vertices
# and the number of edges
ver = 4
edge = 4
gra=[[] for _ in range(ver)]
edgeColors=[-1]*edge
# Enter edge & vertices of edge
# x-- y--
# Since graph is undirected, push both pairs
# (x, y) and (y, x)
# graph[x].append((y, i))
# graph[y].append((x, i))
gra[0].append((1, 0))
gra[1].append((0, 0))
gra[1].append((2, 1))
gra[2].append((1, 1))
gra[2].append((3, 2))
gra[3].append((2, 2))
gra[0].append((3, 3))
gra[3].append((0, 3))
colorEdges(0, gra, edgeColors, isVisited)
# printing all the edge colors
for i in range(edge):
print("Edge {} is of color {}".format(i + 1,edgeColors[i] + 1))
Edge 1 is of color 1 Edge 2 is of color 2 Edge 3 is of color 1 Edge 4 is of color 2
Complejidad temporal: O(N) Donde N es el número de Nodes en el gráfico.
Espacio auxiliar: O(N)
Referencia: https://en.wikipedia.org/wiki/Edge_coloring
Publicación traducida automáticamente
Artículo escrito por AmanSrivastava1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA