¿Cómo calcular el producto escalar de dos vectores?

El vector es una entidad bidimensional con magnitud y dirección. Un vector se puede ver geométricamente como un segmento de línea dirigido con una flecha que indica la dirección y una longitud igual a la magnitud del vector. La dirección del vector es de la cola a la cabeza. Si dos vectores tienen la misma magnitud y dirección, son iguales. Esto indica que si tomamos un vector y lo trasladamos a un nuevo punto (sin rotarlo), el vector que obtenemos al final es el mismo con el que comenzamos.

Producto escalar de dos vectores

El producto de las magnitudes de los dos vectores y el coseno del ángulo entre los dos vectores se llama producto escalar de vectores. El producto escalar de dos vectores produce una resultante que está en el mismo plano que los dos vectores. El producto escalar puede ser un valor real positivo o negativo. El producto punto de dos vectores a y b se representa como:

ab = |a||b|cosθ

Propiedades del producto escalar

• Conmutatividad: 
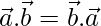
• Distributividad: 
• 
• 
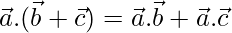
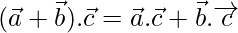
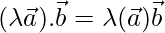
• La raíz cuadrada del producto escalar del vector por sí mismo es igual a la longitud del vector, es decir,  .
• 
• 

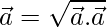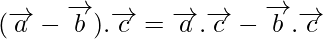
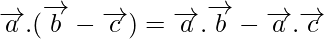
Problemas de muestra

Pregunta 1. Dos vectores con magnitudes 6 y 7 unidades tienen un ángulo de 60 grados entre ellos. Encuentra su producto escalar.

Solución:

Dado: |a| = 6 unidades, |b| = 7 unidades y θ = 60°

Sabemos, producto escalar de dos vectores = |a||b|cosθ

= 6 . (7) . porque(60°)

= 42(½)

⇒ un . b= 21

Pregunta 2. Dos vectores con magnitudes 10 y 5 unidades tienen un ángulo de 60 grados entre ellos. Encuentra su producto escalar.

Solución:

Dado: |a| = 10 unidades, |b| = 5 unidades y θ = 60°

Sabemos, producto escalar de dos vectores = |a||b|cosθ

= 10 . (5) . porque(60°)

= 50(½)

⇒ un . b= 25

Pregunta 3. Dos vectores con magnitudes de 100 y 50 unidades tienen un ángulo de 60 grados entre ellos. Encuentra su producto escalar.

Solución:

Dado: |a| = 100 unidades, |b| = 50 unidades y θ = 60°

Sabemos, producto escalar de dos vectores = |a||b|cosθ

= 100 . (50) . porque(60°)

= 5000(½)

⇒ un . b= 2500

Pregunta 4. Dos vectores con magnitudes 4 y 2 unidades tienen un ángulo de 30 grados entre ellos. Encuentra su producto escalar.

Solución:

Dado: |a| = 4 unidades, |b| = 2 unidades y θ = 30°

Sabemos, producto escalar de dos vectores = |a||b|cosθ

= 4 . (2) . porque(30°)

= 8(√3/2)

⇒ un . b= 4√3

Pregunta 5. Dos vectores con magnitudes 6 y 8 unidades tienen un ángulo de 60 grados entre ellos. Encuentra su producto escalar.

Solución:

Dado: |a| = 6 unidades, |b| = 8 unidades y θ = 60°

Sabemos, producto escalar de dos vectores = |a||b|cosθ

= 6 . (8) . porque(60°)

= 48(1/2)

⇒ un . b= 24

Pregunta 5. Dos vectores con magnitudes 16 y 8 unidades tienen un ángulo de 60 grados entre ellos. Encuentra su producto escalar.

Solución:

Dado: |a| = 16 unidades, |b| = 8 unidades y θ = 60°

Sabemos, producto escalar de dos vectores = |a||b|cosθ

= 16 . (8) . porque(60°)

= 16. (8) . (1/2)

⇒ un . b= 64

Pregunta 6. Dos vectores con magnitudes 20 y 5 unidades tienen un ángulo de 60 grados entre ellos. Encuentra su producto escalar.

Solución:

Dado: |a| = 20 unidades, |b| = 5 unidades y θ = 60°

Sabemos, producto escalar de dos vectores = |a||b|cosθ

= 20 . (5) . porque(60°)

= 20 . (5) . (1/2)

⇒ un . b= 50

Pregunta 7. Dos vectores con magnitudes 30 y 5 unidades tienen un ángulo de 60 grados entre ellos. Encuentra su producto escalar.

Solución:

Dado: |a| = 30 unidades, |b| = 5 unidades y θ = 60°

Sabemos, producto escalar de dos vectores = |a||b|cosθ

= 30 . (5) . porque(60°)

= 15. (5) . 

⇒ un . b= 75