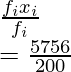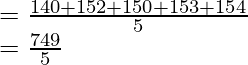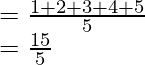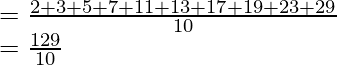La media o promedio de la distribución de datos dada es el valor central calculado. Se utiliza para determinar el promedio de los datos dados. Da una medida de la tendencia central de los datos. La tendencia central de la distribución de datos es la medida estadística que representa e identifica toda la distribución de datos utilizando un solo valor. Actúa como un descriptor exacto de los datos representados.
En estadística, la media de los datos también se puede definir como la suma de todas las observaciones al número total de observaciones. La media de distribución de datos también se conoce como media aritmética o promedio. Se denota por x̄.
⇒ Dado un conjunto de datos con n valores totales,
X = x 1 , x 2 ,…, x n , la media x̄ es la media de los n valores x 1 , x 2 ,…, x n .
fórmula media
![]()
Fórmula media para datos no agrupados
La fórmula para calcular la media en caso de datos no agrupados:
Supongamos, x 1 , x 2 , x 3 ,……, x n ser n observaciones de un conjunto de datos.
Entonces tenemos,
La media de estos valores es:
Aquí tenemos,
x i = i-ésima observación, 1 ≤ i ≤ norte
∑x i = Suma de observaciones
n = Número de observaciones
Fórmula media para datos agrupados
La media de los datos depende del cálculo de la media en el caso de datos agrupados:
- Método directo
- Método de la media supuesta
- Método de desviación escalonada
Cálculo de la media usando el método directo
El método directo es uno de los métodos más fáciles y sencillos que se utilizan para calcular la media de los datos agrupados. Los siguientes pasos se pueden utilizar para calcular la media de la distribución de datos dada:
Paso 1: Cree una tabla que tenga cuatro columnas como se calcula a continuación,
Columna 1- Intervalo de clase.
Columna 2- Marcas de clase, indicadas por xi.
Columna 3- Frecuencias correspondientes (f i )
Columna 4- x i f i, que es el producto de la columna 2 y la columna 3.
Paso 2: Calculando la media con la fórmula Media, tenemos = ![]()
Cálculo de la media utilizando el método de la media supuesta
El método directo utilizado para el cálculo de la media es un método tedioso. El método de la media supuesta se puede utilizar para calcular la media de un conjunto de datos agrupados. Los siguientes pasos se pueden utilizar para calcular la media de la distribución de datos dada:
Paso 1: Cree una tabla que tenga cinco columnas como se calcula a continuación,
Columna 1- Intervalo de clase.
Columna 2- Marcas de clase, indicadas por xi. El valor central de esta columna se toma como la media supuesta. Esto se denota con A.
Columna 3: luego se calculan las desviaciones correspondientes. Los valores de la columna se calculan de la siguiente manera, es decir, d i = x i – A
Columna 4- Frecuencias correspondientes (f i )
Columna 5- La media de los valores d i de la Columna 3 se calcula utilizando la fórmula. Por lo tanto, la media de d i = ![]()
Paso 2: Por último, calcule la media de la distribución de datos dada realizando la suma de los datos para encontrar la media supuesta de la media de d i .
Cálculo de la media usando el método de desviación escalonada
También conocido como el método de cambio de origen y escala, el método de desviación de paso se utiliza para eliminar la realización de cálculos tediosos para el cálculo de la media de datos agrupados. Los siguientes pasos se pueden utilizar para calcular la media de la distribución de datos dada:
Paso 1: Cree una tabla que contenga cinco columnas como se indica a continuación,
Columna 1- Intervalo de clase.
Columna 2- Marcas de clase, indicadas por x i . El valor central de esta columna se toma como la media supuesta. Esto se denota con A.
Columna 3: luego se calculan las desviaciones correspondientes. Los valores de la columna se calculan de la siguiente manera, d i = x i – A
Columna 4- Calcular los valores de u i usando la fórmula, u i = ![]() , donde h es el ancho de clase.
, donde h es el ancho de clase.
Columna 5- Frecuencias Correspondientes (f i )
Paso 2: Por lo tanto, la Media de u i = ![]()
Paso 3: Por último, calcule la media de la distribución de datos dada calculando la media realizando la suma de la media A supuesta al producto del ancho de clase (h) con la media de u i .
Ejemplos de preguntas
Pregunta 1. Calcula la media de los siguientes datos.
5, 10, 4, 20, 25, 18, 11, 13, 19, 22
Solución:
Aquí nos han dado,
x yo = 5, 10, 4, 20, 25, 18, 11, 13, 19, 22
norte = 10
Media x̄ =
=
=
= 14,7
Por eso,
La media de estos datos es 14,7.
Pregunta 2. ¿Calcular la media de los datos para la siguiente distribución de notas obtenidas por los alumnos en los exámenes?
| Marcas | 50 | 86 | 76 | 84 | 66 | 56 | 58 | 40 |
| Numero de estudiantes | 40 | 2 | 8 | 4 | 30 | 48 | 56 | 12 |
Solución:
Encontrar la suma:
Marcas ( xi ) Número de estudiantes (f i ) arreglar yo x yo 50 40 1000 86 2 86 76 8 304 84 4 168 66 30 990 56 48 1344 58 56 1624 40 12 240 Suma 200 5756 Media =
= 28,78
Por lo tanto,
La media de la siguiente distribución es 28,78.
Pregunta 3. Suponga que en una clase la altura de 5 niñas es de 140 cm, 152 cm, 150 cm, 153 cm y 154 cm. Luego encuentra la media de la altura de las niñas.
Solución:
Aquí nos dan altura de chicas
140 cm, 152 cm, 150 cm, 153 cm y 154 cm
= 149,8
Por lo tanto,
Media, x̄ =149,8 cm.
Pregunta 4. ¿Encuentre la media de los primeros cinco números naturales?
Solución:
Los primeros cinco naturales son 1, 2, 3, 4 y 5
Más lejos,
Media de los cinco primeros números naturales =
= 3
De este modo,
La media de los cinco primeros números naturales es 3.
Pregunta 5. ¿Encuentre la media de los primeros 10 números primos?
Solución:
Los primeros 10 números primos son 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Más lejos,
Media de los cinco primeros números naturales =
= 12,9
De este modo,
La media de los 10 primeros números primos es 12,9.
Publicación traducida automáticamente
Artículo escrito por yashkumar0457 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA