La raíz cuadrada de cualquier valor numérico es un valor que al auto multiplicarse da como resultado el número original. ‘√’ es el símbolo radical que se usa para representar la raíz de cualquier número. Por raíz cuadrada, nos referimos a una potencia de 1/2 de ese número. Por ejemplo, supongamos que x es la raíz cuadrada de cualquier número entero y, esto implica que x=√y. Al multiplicar la ecuación, también obtenemos x 2 = y.
La raíz cuadrada del cuadrado de un número positivo da el número original.
Para entender el concepto, sabemos que el cuadrado de 4 es 16 y la raíz cuadrada de 16, √16 = 4. Ahora, como podemos ver, 16 es una figura cuadrada perfecta. Esto facilita el cálculo de la raíz cuadrada de dichos números. Sin embargo, para calcular la raíz cuadrada de un cuadrado imperfecto como 3, 5, 7, etc., calcular la raíz es un proceso difícil.
Una función de raíz cuadrada es una función uno a uno que usa como entrada un número positivo y devuelve la raíz cuadrada del número de entrada dado.
f(x) = √x
Propiedades de las raíces cuadradas:
Algunas de las propiedades importantes de la raíz cuadrada son las siguientes:
- Para un número cuadrado perfecto, existe una raíz cuadrada perfecta.
- Para un número que termina con un número par de ceros, existe una raíz cuadrada.
- La raíz cuadrada de cualquier número negativo no está definida.
- Para un número que termina con los dígitos 2, 3, 7 u 8, la raíz cuadrada perfecta no existe.
- Para un número que termina con los dígitos 1, 4, 5, 6 o 9, entonces el número tendrá una raíz cuadrada.
¿Cómo calcular una raíz cuadrada?
Los números cuadrados perfectos son números enteros de naturaleza positiva y se pueden expresar fácilmente en forma de la multiplicación de un número por sí mismo. Los números cuadrados perfectos se representan como el valor de la potencia 2 de cualquier número entero. El cálculo de la raíz cuadrada de números cuadrados perfectos es relativamente más fácil. Existen principalmente cuatro métodos utilizados para encontrar la raíz cuadrada de los números:
- Método de resta repetida de la raíz cuadrada
- Método de raíz cuadrada por factorización prima
- Raíz cuadrada por método de estimación
- Método de raíz cuadrada por división larga
Los tres métodos anteriores se pueden utilizar en el cálculo de la raíz cuadrada de números cuadrados perfectos. El último método, sin embargo, se puede utilizar para ambos tipos de números.
Método de resta repetida de raíces cuadradas
El método se basa en la siguiente secuencia de pasos:
Paso 1: Resta los números impares consecutivos del número para el que estamos encontrando la raíz cuadrada.
Paso 2: Repita el paso 1 hasta alcanzar un valor de 0.
Paso 3: El número de veces que se repite el paso 1 es la raíz cuadrada requerida del número dado.
Nota: Este método solo se puede usar para cuadrados perfectos.
Por ejemplo, para el número 16, el método funciona de la siguiente manera:
16 – 1 = 15
15 – 3 = 12
12 – 5 = 7
7- 7 = 0
El proceso se repite 4 veces. Por lo tanto, √16 = 4.
Método de raíz cuadrada por factorización prima
La descomposición en factores primos de cualquier número es la representación de ese número en la forma de un producto de números primos. El método se basa en la siguiente secuencia de pasos:
Paso 1: Divide el número especificado en sus factores primos.
Paso 2: Se forma un par de factores similares de tal manera que ambos factores en cada uno de los pares formados sean iguales.
Paso 3: Toma un factor de cada uno de los pares.
Paso 4: El producto de los factores se obtiene tomando un factor de cada par.
Paso 5: Este producto obtenido es la raíz cuadrada del número dado.
Nota: Este método solo se puede usar para cuadrados perfectos.
Por ejemplo, para el número 64, el método funciona de la siguiente manera:

64 = {2 × 2} × {2 × 2} × {2 × 2}
64 = 2 2 × 2 2 × 2 2
64 = (2 × 2 × 2) 2
64 = (8) 2
√64 = 8
Raíz cuadrada por método de estimación
El método de estimación se utiliza para aproximar la raíz cuadrada de un número dado. Aproxima la raíz cuadrada de un número a una suposición razonable del valor real. Los cálculos son más fáciles en este método. Sin embargo, es un proceso realmente largo y lento.
Paso 1: Encuentre el cuadrado perfecto más cercano que ocurra tanto antes como después del número dado.
Paso 2: encuentra los siguientes enteros más cercanos y redondea cada vez para llegar a la respuesta más cercana.
Por ejemplo, para el número 15, el método funciona de la siguiente manera:
9 y 16 son los números cuadrados perfectos antes y después más cercanos a 15. Ahora, sabemos,
√16 = 4 y √9 = 3. Esto implica que la raíz cuadrada del número 15 se encuentra entre 3 y 4. Ahora, el proceso consiste en evaluar si la raíz cuadrada del número 15 está más cerca de 3 o de 4.
El primer caso es tomar 3,5 y 4. El cuadrado de 3,5 = 12,25 y la raíz cuadrada de 4 = 16. Por lo tanto, la raíz cuadrada del entero 15 se encuentra entre 3,5 y 4 y está más cerca de 4.
Además, encontramos los cuadrados de 3,8 y 3,9, que equivalen a 3,8 2 = 14,44 y 3,9 2 = 15,21 respectivamente. Esto implica que √15 se encuentra entre 3,8 y 3,9. En una evaluación adicional, obtenemos que √15 = 3.872.
Método de raíz cuadrada por división larga
El método de división larga para el cálculo de la raíz cuadrada de números involucra la división de números grandes en pasos o partes, dividiendo así el problema en una secuencia de pasos más fáciles.
Por ejemplo, para el número 180, el método funciona de la siguiente manera:
Paso 1: Se coloca una barra sobre cada par de dígitos del número que comienza con el lugar de la unidad.
Paso 2: El número más a la izquierda se divide por el número más grande de modo que el cuadrado sea menor o igual que el número en el par más a la izquierda.

Paso 3: Ahora, se baja el número debajo de la siguiente barra a la derecha del resto. El último dígito del cociente obtenido se suma al divisor. Ahora, el siguiente paso es encontrar un número a la derecha de la suma obtenida, tal que junto con el resultado de la suma, forme un nuevo divisor para el nuevo dividendo.

Paso 4: El número obtenido en el cociente es equivalente al número seleccionado en el divisor.
Paso 5: Se repite el mismo proceso usando un punto decimal y agregando ceros en pares al resto.

Paso 6: El cociente forma la raíz cuadrada del número.
Ejemplos de preguntas
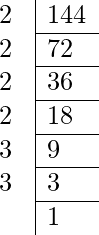
Pregunta 1. ¿Calcular la raíz cuadrada de 144 por el método de factorización prima?
Solución:
144 = {2 × 2} × {2 × 2} × {3 × 3}
144 = 2 2 × 2 2 × 3 2
144 = (2 × 2 × 3) 2
144 = (12) 2
√144 = 12
Pregunta 2. ¿Cuál es la forma de simplificar la raíz cuadrada?
Solución:
La descomposición en factores primos del número dado se puede calcular. En caso de que el factor no se pueda agrupar, se utiliza un símbolo de raíz cuadrada para agruparlos. La siguiente regla se utiliza para la simplificación:
√xy = √(x × y), donde x e y son números enteros positivos.
Por ejemplo, √12 =
= 2√3
En el caso de fracciones, se utiliza la siguiente regla:
Por ejemplo:
= √5
Pregunta 3. Resuelve: √(x + 2) = 4
Solución:
Sabemos,
√(x + 2) = 4
Al elevar al cuadrado ambos lados, obtenemos;
X + 2 = √4
x + 2 = ±4
x = ±4 – 2
Por lo tanto, tenemos,
x = 2 o x = -6
Pregunta 4. ¿La raíz cuadrada de un número negativo puede ser un número entero? Explique.
Solución:
Sabemos que los números negativos no pueden tener una raíz cuadrada. La razón detrás de esto es que si se multiplican dos números negativos, el resultado obtenido siempre será un número positivo. Por lo tanto, la raíz cuadrada de un número negativo estará en forma de número complejo.
Pregunta 5. ¿Calcular la raíz cuadrada de 25 por el método de resta repetida?
Solución:
Siguiendo los pasos indicados anteriormente, tenemos,
25 – 1 = 24
24 – 3 = 21
21 – 5 = 16
16 – 7 = 9
9 – 9 = 0
Dado que el proceso se repite 5 veces, tenemos, √25 = 5.
Pregunta 6. ¿Calcular la raíz cuadrada de 484 por el método de división larga?
Solución:
Por el método de división larga, tenemos,
Ahora,
El resto es 0, por lo tanto, 484 es un número cuadrado perfecto, tal que,
√484 = 22
Publicación traducida automáticamente
Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA