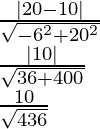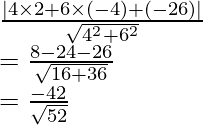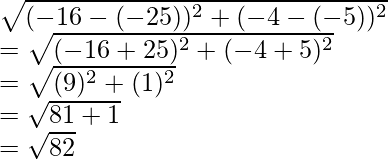La longitud del cable utilizado para cubrir la longitud entre dos puntos es la distancia entre dos puntos. En caso de que los dos puntos estén situados en la misma línea horizontal o vertical, la distancia entre los dos puntos se puede calcular restando las coordenadas que no son iguales.
La fórmula de distancia se puede utilizar para calcular la distancia que se mide entre los dos segmentos de línea. La fórmula de la distancia se puede usar para calcular la suma de las longitudes de todos los lados de un polígono, el perímetro de los polígonos en un plano de coordenadas, el área de los polígonos, etc. Las longitudes de los lados de los triángulos también se pueden calcular usando la fórmula fórmula de distancia El tipo de triángulo, escaleno, isósceles o equilátero también se puede determinar mediante la fórmula de la distancia.
Distancia entre dos puntos
La coordenada x del punto se conoce como abscisa, mientras que la coordenada y se conoce como ordenada. La fórmula de la distancia se puede utilizar para calcular la distancia entre dos puntos del plano xy. Un par ordenado (x, y) representa la coordenada del punto, donde la coordenada x se define como la distancia del punto desde el eje x y la coordenada y es la distancia del punto desde el eje y.
La siguiente fórmula se puede utilizar para encontrar la distancia entre dos puntos en un plano 2d:
Considere dos puntos arbitrarios cualesquiera A(x 1 ,y 1 ) y B(x 2 ,y 2 ) en el eje de coordenadas dado. La distancia entre los siguientes dos puntos se da de la siguiente manera:

re = ![]()
¿Cómo derivar la fórmula de la distancia?
Prueba:
En el triángulo rectángulo ABC tenemos,
Por el teorema de Pitágoras,
AB2 = AC2 + BC2 _
Dado que hemos derivado la fórmula de cálculo de la distancia entre dos puntos, por lo tanto,
La distancia entre los puntos A y C se calcula como (x 2 – x 1 ) 2
La distancia entre los puntos A y C se calcula como (y 2 – y 1 ) 2
La distancia, d se calcula como,
re 2 = (x 2 – x 1 ) 2 + (y 2 – y 1 ) 2
Ahora,
Tomando la raíz cuadrada en ambos lados,
re =
Esta es la llamada fórmula de la distancia entre dos puntos.
Fórmula de distancia de punto a línea
Un punto (x 1, y 1 ) y una recta ax + by + c = 0
re =
Fórmula de distancia entre dos rectas paralelas
Dos rectas paralelas ax + by + c 1 = 0 y ax + by + c 2 = 0
re =
Ejemplos de preguntas
Pregunta 1. Calcula la distancia entre los puntos X(5, 15) e Y(4, 14)
Solución:
Aquí para encontrar la distancia entre el punto A y B
Aplicando fórmula de distancia
re =
re =
La distancia entre X e Y es √2 o 1.41
Pregunta 2. Encuentra la distancia entre las líneas paralelas -6x + 20y + 10 = 0 y -6x + 20y + 20 = 0.
Solución:
La ecuación general de las rectas paralelas es
Ax + By + C 1 = 0 y Ax + By + C 2 = 0,
Aquí,
A = -6,
B = 20,
C 1 = 10 y
C2 = 20.
Aplicando fórmula
re =
re =
d = 10/√436
Pregunta 3. Calcula la distancia entre la línea 4a + 6b – 26 = 0 desde el punto (2, –4).
Solución:
La ecuación general de las rectas paralelas es
Un punto (x 1 , y 1 ) y una recta ax + by + c = 0
Aquí,
A = 4, B = 6 y C = –26
Aplicando fórmula
re =
re =
d = -42/√52
Pregunta 4. ¿Calcular la distancia entre los puntos A(-25, -5) y B(-16, -4)?
Solución:
Aquí para encontrar la distancia entre el punto A y B
Aplicando fórmula de distancia
re =
re =
La distancia entre A y B es √82 o 9.05.