La geometría es una rama de las matemáticas tan antigua como la aritmética misma. Trata de las propiedades de las figuras, sus medidas, la distancia entre dos formas o puntos y sus posiciones relativas. En otras palabras, la geometría es una rama de las matemáticas que se ocupa de superficies, puntos, formas, planos, coordenadas, etc. Todo tipo de forma observada en la naturaleza cae dentro del ámbito de la geometría. Ayuda a medir varias proporciones de todas esas formas y calcular sus áreas, volúmenes y otros parámetros asociados con ellos. No solo ayuda a uno a mantenerse alejado de la teoría matemática, sino que también resulta útil en la vida diaria.
Triángulo
Un triángulo se define como una forma plana que se obtiene uniendo tres puntos, dos de los cuales no son colineales. En caso de que los tres puntos resulten ser colineales, la figura resultante no se llamaría triángulo. Como sugiere su nombre, un triángulo tiene tres ángulos, cuya suma siempre mide 180 grados. Dado que es una figura cerrada formada por la unión de tres puntos coplanares, un triángulo es una forma bidimensional, lo que implica que es una forma plana sin espesor.
La siguiente figura representa un triángulo ABC con tres vértices AB, BC y CA.

tipos de triangulos
- Triángulo Escaleno: Un triángulo escaleno es aquel cuyos lados son desiguales, es decir, tienen una medida distinta. Como resultado, todos estos lados están inclinados en diferentes ángulos entre sí. Por lo tanto, los triángulos escalenos tienen lados y ángulos que tienen diferentes medidas.

- Triángulo isósceles: Un triángulo isósceles es aquel cuyos dos lados son iguales y los ángulos opuestos a los lados iguales también son iguales en medida.

- Triángulo Equilátero: Un triángulo equilátero es aquel cuyos tres lados, así como sus ángulos, miden igual. Dado que la propiedad de la suma de los ángulos de un triángulo establece que la suma de los tres ángulos de un triángulo mide 180 grados, cada ángulo de un triángulo equilátero mide 60 grados.

- Triángulo Rectángulo: Un triángulo rectángulo es aquel cuyos lados miden diferente, siendo los dos lados más cortos perpendiculares entre sí. El lado más largo se llama hipotenusa.

perímetro de un triángulo
El perímetro de cualquier espacio cerrado se refiere a la longitud alrededor de sus lados. Sumar la longitud de todos los lados de una forma daría como resultado su perímetro. De manera similar, el perímetro de un triángulo se puede calcular sumando las longitudes de sus tres lados.
Perímetro de un triángulo regular ABC = AB + BC+ CA
La fórmula anterior se puede simplificar aún más para un triángulo equilátero de la siguiente manera:
Perímetro de un triángulo equilátero de lado a = a + a + a = 3a.
Área de un Triángulo
El área de un triángulo se puede calcular de diferentes maneras dependiendo del tipo de triángulo. Estos métodos son los siguientes:
1. El área de un triángulo se puede calcular con la ayuda de las longitudes de su base y altura de la siguiente manera:
Área de un triángulo dada su base y altura = 1/2 × b × h
2. La fórmula anterior se puede usar para triángulos escalenos, isósceles y rectángulos. Pero en el caso de un triángulo equilátero, la fórmula para calcular el área es:
Área de un triángulo equilátero de lado a =
3. A veces, se debe aplicar la fórmula de Heron para calcular el área de un triángulo escaleno en ausencia de información sobre las medidas de sus ángulos y la longitud de su altura.
Área de un triángulo usando la Fórmula de Heron =
, donde s es el semiperímetro del triángulo dado y a, b, c representan las longitudes de los lados del triángulo dado.
Problemas de muestra
Pregunta 1. Encuentra el perímetro y el área de un triángulo equilátero de 6 cm de lado.
Solución:
Perímetro de un triángulo equilátero = 3a = 3(6) = 18 cm
Área de un triángulo equilátero =
=
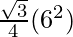
= 9√3 cm cuadrados
Por lo tanto, perímetro = 18 cm y área = 9√3 cm cuadrados.
Pregunta 2. Encuentra el perímetro de un triángulo rectángulo cuya base mide 3 cm y la hipotenusa mide 5 cm.
Solución:
Según el Teorema de Pitágoras, (hipotenusa) 2 = (base) 2 + (perpendicular) 2
⇒
= perpendicular
⇒ perpendiculares = 4 cm
Entonces, perímetro del triángulo = 4 + 3 + 5 cm
= 12 centímetros
Por lo tanto, el perímetro del triángulo dado es de 12 cm.
Pregunta 3. Encuentra el área de un triángulo cuya base es de 40 cm y la altura es de 12 cm.
Solución:
Área de un triángulo dada su base y altura = 1/2 × b × h
= 1/2 × 40 × 12
= 240 cm2
Por lo tanto, el área del triángulo dado es de 240 cm2.
Pregunta 4. Encuentra el lado de un triángulo equilátero cuyo perímetro es de 75 cm.
Solución:
Perímetro de un triángulo equilátero = 3a
3a = 75 o a = 25 cm
Por lo tanto, el lado del triángulo mide 25 cm.
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA