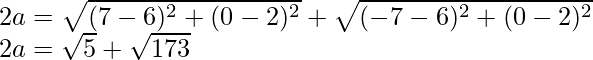Cuando un plano cruza un cono, se crean secciones cónicas, también conocidas como cónicas. La geometría de estas secciones está determinada por el ángulo en el que se cruzan. Como resultado, las secciones cónicas se dividen en cuatro categorías: círculo, elipse, parábola e hipérbola. Cada una de estas formas tiene su propio conjunto de características y ecuaciones matemáticas. La elipse se analiza a continuación.
Elipse
Como sección cónica, una elipse es una forma que se forma cuando un plano se cruza con un cono en un ángulo (β) menor que el ángulo recto pero mayor que el ángulo formado en el vértice de un cono (α). En otras palabras, se forma una elipse cuando un plano corta un cono en un ángulo β tal que α<β<90 o .

Como se muestra en la figura anterior, un cono y un plano se intersecan en un ángulo β que es menor que el ángulo recto pero mayor que α para formar una elipse debido a la intersección.
Ecuación de una elipse
- La ecuación estándar de una elipse centrada en (h, k) con un eje mayor paralelo al eje x viene dada por:
,
donde las coordenadas del vértice son (h±a, 0), las coordenadas del co-vértice son (h, k±b) y las coordenadas de los focos son (h±c, k), donde c 2 = a 2 – b 2 .

elipse horizontales
- La ecuación estándar de una elipse centrada en (h, k) con un eje mayor paralelo al eje y viene dada por:
,
donde las coordenadas del vértice son (h, k±a), las coordenadas del co-vértice son (h±b, k) y las coordenadas de los focos son (h, k±c), donde c 2 = a 2 – b 2 .

elipse vertical
¿Cómo encontrar la ecuación de una elipse con focos y puntos?
Solución:
Para encontrar la ecuación de una elipse, necesitamos los valores a y b. Ahora bien, se sabe que la suma de las distancias de un punto situado sobre una elipse a sus focos es igual a la longitud de su eje mayor, 2a. El valor de a puede ser calculado por esta propiedad. Para calcular b, usa la fórmula c 2 = a 2 – b 2 . Sustituya los valores obtenidos de a y b en la forma estándar para obtener la ecuación requerida.
Comprendamos este método con más detalle a través de un ejemplo.
Ejemplo: digamos, una elipse que pasa por el origen con focos (±4, 0) y punto (–4, 1.8).
Usando la fórmula, tenemos
2a = 10
un = 5
Ponga a = 5 en c 2 = a 2 – b 2 para encontrar b.
b 2 = 25 – 16
b 2 = 9
Como la elipse se encuentra en el eje x, la ecuación tiene la forma
.
Entonces, la ecuación es,
.
Problemas similares
Pregunta 1. Encuentra la ecuación de una elipse que pasa por el origen con focos (±7, 0) y punto (6, 2).
Solución:
Usando la fórmula, tenemos
2a = 15,74
= 7,87
Ponga a = 7.87 en c 2 = a 2 – b 2 para encontrar b.
b2 = 62 – 49
b 2 = 13
Como la elipse se encuentra en el eje x, la ecuación tiene la forma
.
Entonces, la ecuación es,
.
Pregunta 2. Encuentra la ecuación de una elipse que pasa por el origen con focos (±5√3, 0) y punto (6, 4).
Solución:
Usando la fórmula, tenemos
2a = 20
un = 10
Ponga a = 10 en c 2 = a 2 – b 2 para encontrar b.
b2 = 100 – 75
b 2 = 25
Como la elipse se encuentra en el eje x, la ecuación tiene la forma
.
Entonces, la ecuación es,
.
Pregunta 3. Encuentra las coordenadas del eje mayor de la elipse con focos (0, ±5) y eje menor (12, 0).
Solución:
Tenemos, c = 5 y b = 12.
Póngalos en c 2 = a 2 – b 2 para encontrar a.
un 2 = 12 2 + 5 2
un 2 = 169
un = 13
Las coordenadas del eje mayor son (0, ±13).
Pregunta 4. Encuentra la ecuación de la elipse que pasa por el origen si a = 3, b = 5 y el eje mayor es paralelo al eje x.
Solución:
El eje mayor es paralelo al eje x, por lo que la elipse se encuentra en el eje x.
La ecuación es de la forma
.
Aquí, a = 3, b = 5, h = 0 y k = 0.
Entonces, la ecuación se convierte en,
Pregunta 5. Encuentra la ecuación de la elipse que pasa por el origen si a = 13, b = 5, y el eje menor es paralelo al eje x.
Solución:
El eje mayor es paralelo al eje x, por lo que la elipse se encuentra en el eje x.
La ecuación es de la forma
.
Aquí a = 13 y b = 5, h = 0 y k = 0.
Entonces, la ecuación se convierte en,