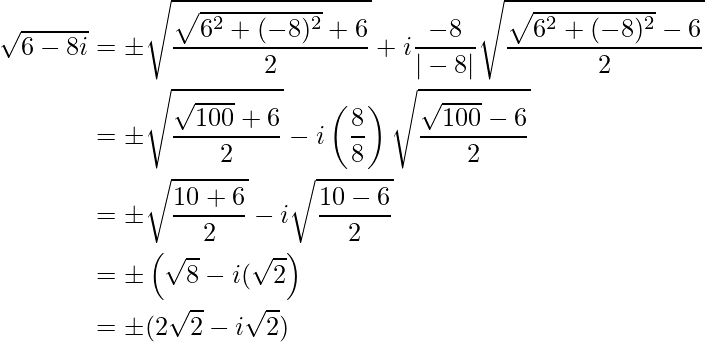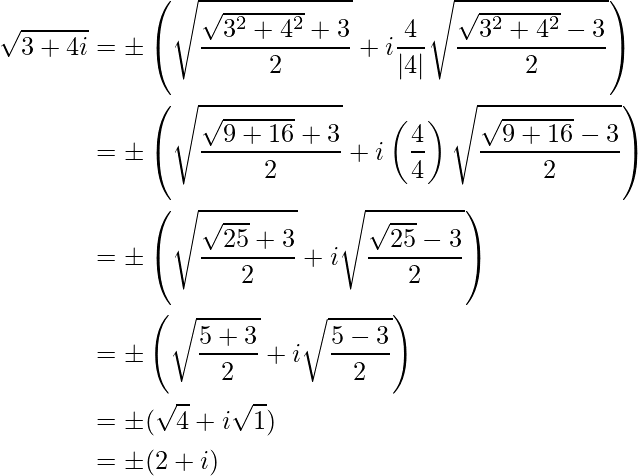¿Cómo encontrar la raíz cuadrada de un número?

Posted on by Rudeus Greyrat

En situaciones cotidianas se enfrenta el reto de calcular la raíz cuadrada de un número. ¿Qué pasa si uno no tiene acceso a una calculadora o cualquier otro aparato? Se puede hacer con papel y lápiz a la antigua en un estilo de división larga. Sí, hay una variedad de maneras de hacerlo. Comencemos discutiendo primero la raíz cuadrada y sus propiedades.

¿Qué es una raíz cuadrada?

Una raíz cuadrada es un valor que le da al número original esa multiplicación de sí mismo. por ejemplo, 6 multiplicado por sí mismo da 36 (es decir, 6 × 6 = 36), por lo tanto, 6 es la raíz cuadrada de 36 o, en otras palabras, 36 es el número cuadrado de 6.

Supongamos que a es la raíz cuadrada de b, entonces se representa como,

a = √b o  

un 2 = segundo

Deje que el cuadrado de 2 sea 4, por lo que la raíz cuadrada de 4 será 2, es decir 

√4 = 2

Las siguientes son raíces cuadradas de los primeros 50 dígitos como:

Raíz cuadrada

Valor 

Raíz cuadrada

Valor 

√1

1

√26

5.0990

√2

1.4142

√27

5.1962

√3

1.7321

√28

5.2915

√4

2

√29

5.3852

√5

2.2361

√30

5.4772

√6

2.4495

√31

5.5678

√7

2.6458

√32

5.6569

√8

2.8284

√33

5.7446

√9

3

√34

5.8310

√10

3.1623

√35

5.9161

√11

3.3166

√36

6

√12

3.4641

√37

6.0828

√13

3.6056

√38

6.1644

√14

3.7417

√39

6.2450

√15

3.8730

√40

6.3246

√16

4

√41

6.4031

√17

4.1231

√42

6.4807

√18

4.2426

√43

6.5574

√19

4.3589

√44

6.6332

√20

4.4721

√45

6.7082

√21

4.5826

√46

6.7823

√22

4.6904

√47

6.8557

√23

4.7958

√48

6.9282

√24

4.8990

√49

7

√25

5

√50

7.0711

Por lo tanto, la raíz cuadrada del cuadrado de un número positivo da el número original. Sin embargo, la raíz cuadrada de un número negativo representa un número complejo.

Propiedades de la raíz cuadrada 

  • Una raíz cuadrada perfecta siempre existe si un número es un cuadrado perfecto.
  • La raíz cuadrada de 4 es 2 y la raíz cuadrada de 16 es 4. Entonces podemos concluir que la raíz cuadrada de un cuadrado par perfecto es par.
  • La raíz cuadrada de 9 es 3 y la raíz cuadrada de 81 es 9. Entonces podemos concluir que la raíz cuadrada de un cuadrado perfecto impar es impar.
  • Un cuadrado perfecto no puede ser negativo y, por lo tanto, la raíz cuadrada de un número negativo no está definida.
  • Del punto anterior, se puede concluir que los números que terminan en (que tienen dígito de la unidad) 1, 4, 5, 6 o 9 tendrán una raíz cuadrada.
  • Si un número de termina con un número par de ceros (0), entonces puede tener una raíz cuadrada.
  • Si el dígito unitario de un número es 2, 3, 7 u 8, entonces no es posible una raíz cuadrada perfecta.
  • Si un número termina en 2, 3, 7 u 8 (en el dígito unitario), entonces la raíz cuadrada perfecta no existe.
  • Los dos valores de la raíz cuadrada se pueden multiplicar. Por ejemplo, √5 se puede multiplicar por √2, entonces el resultado debería ser √10.
  • Dos raíces cuadradas iguales se multiplican para dar un número que no es raíz cuadrada. Cuando √5 se multiplica por √5 obtenemos como resultado 5.

Cuadrado perfecto 

Un número que se puede expresar como el producto de dos enteros idénticos se llama cuadrado perfecto. Los cuadrados perfectos son números que se pueden formar elevando al cuadrado cualquier número entero.

p.ej: 

9 es un cuadrado perfecto porque es el producto de dos enteros iguales, 3 × 3 = 9. 

Sin embargo, 10 no es un cuadrado perfecto porque no se puede expresar como el producto de dos enteros iguales. (5 × 2 = 10). 

Así, un cuadrado perfecto es un número entero que es el cuadrado de un número entero; en otras palabras, es el producto de algún número entero consigo mismo.

Los números que son cuadrados perfectos se mencionan a continuación, y encontrar las raíces cuadradas de esos números es fácil. Aquí hay algunos ejemplos de raíces cuadradas:

  • 1 2 = 1
  • 2 2 = 4
  • 3 2 = 9
  • 4 2 = 16
  • 5 2 = 25
  • 6 2 = 36
  • 7 2 = 49
  • 8 2 = 64
  • 9 2 = 81
  • 10 2 = 100

Como resultado, los cuadrados completos son 1, 4, 9, 16, 25, 36, 49, 64, 81 y 100. 

Métodos para encontrar la raíz cuadrada de un número

Para determinar si un número dado es un cuadrado perfecto o un cuadrado imperfecto, primero debemos determinar si es un cuadrado perfecto o un cuadrado imperfecto. Si el número es un cuadrado perfecto, como 4, 9, 16, etc., usaremos el proceso de factorización prima para factorizarlo. Debemos usar el método de división larga para encontrar la raíz si el número es un cuadrado incompleto, como 2, 3, 5, etc.

  1. Método de resta repetida
  2. Método de factorización prima
  3. Método de división

1. Método  de resta repetida

Se sabe que la suma de los primeros n números naturales impares es n 2 . Haremos esto para calcular la raíz cuadrada de un número entero restándolo varias veces. Consideremos un ejemplo y veamos cómo funciona este enfoque. Digamos que debes encontrar la raíz cuadrada de 25, que es √25. Los pasos son los siguientes:

Consideremos los siguientes ejemplos para comprender el método de resta repetida para determinar las raíces cuadradas.

Ejemplo 1: Determina la raíz cuadrada de 25 usando el método de resta repetida.
Solución:

Ya que 25 es un número impar. Por lo tanto, los pasos para encontrar la raíz cuadrada de 25 son:

  • 25 – 1 = 24
  • 24 – 3 = 21
  • 21 – 5 = 16
  • 16- 7 = 9
  • 9 – 9 = 0

Aquí se necesitan cinco pasos para obtener el 0. 

Por lo tanto, la raíz cuadrada de 25 es 5 .

Ejemplo 2: Determina la raíz cuadrada de 16 usando el método de resta repetida.
Solución:

Ya que 16 es un número par. Por lo tanto, los pasos para encontrar la raíz cuadrada de 16 son:

  • 16 – 4 = 12
  • 12 – 4 = 8
  • 8 – 4 = 4

Aquí se necesitan cuatro pasos para obtener el 0. 

Por lo tanto, la raíz cuadrada de 16 es 4 .

Ejemplo 3: Encuentra la raíz cuadrada de 49 usando el método de resta repetida.

Solución:

Como 49 es un número impar. Por lo tanto, los pasos para encontrar la raíz cuadrada de 49 son:

  • 49 – 1 = 48
  • 48 – 3 = 45
  • 45 – 5 = 40
  • 40 – 7 = 33
  • 33 – 9 = 24
  • 24 – 11 = 13
  • 13 -13 = 0

Aquí se necesitan siete pasos para obtener el 0. 

Por lo tanto, la raíz cuadrada de 49 es 7 .

2. Método de factorización prima 

El método de descomposición en factores primos consiste en expresar números en función de sus factores primos. La raíz cuadrada del número viene dada por el producto de un elemento de cada par de factores primos iguales. Este enfoque también se puede utilizar para determinar si un número dado es un cuadrado perfecto o no. Este método, sin embargo, no se puede usar para encontrar la raíz cuadrada de números decimales cuadrados no perfectos.

ej.: Los factores primos de 126 serán 2, 3 y 7 ya que 2 × 3 × 3 × 7 = 126 y 2, 3, 7 son números primos.

  • 16 = 2 × 2 × 2 × 2 = 2 2 × 2 2 = √16 = 4
  • 25 = 5 × 5 = 5 2 = √25 = 5
  • 64 = 2 × 2 × 2 × 2 × 2 × 2 = √64 = 8

3. Método de división 

Cuando los números enteros son lo suficientemente grandes, es fácil obtener la raíz cuadrada de un cuadrado perfecto utilizando el enfoque de división larga, porque obtener sus raíces cuadradas mediante la factorización se vuelve largo y complicado. Para superar este problema, se desarrolla un nuevo método para encontrar la raíz cuadrada. Este método utiliza básicamente la operación de división por un divisor cuyo cuadrado es menor o igual que el dividendo.

Los siguientes son los pasos para el método de división:

Paso 1: Tomar el número cuya raíz cuadrada se va a encontrar. Coloque una barra sobre cada par de dígitos del número a partir del lugar de la unidad (lado más a la derecha).

Paso 2: dividamos el número más a la izquierda por el número más grande cuyo cuadrado es menor o igual que el número debajo de la barra más a la izquierda. Toma este número como el divisor y el cociente. El número debajo de la barra más a la izquierda se considera el dividendo.

Paso 3: Divide y obtén el número. Baje el número debajo de la siguiente barra a la derecha del resto.

Paso 4: Duplica el divisor (o suma el divisor a sí mismo). A la derecha de este divisor, busque un número adecuado que, junto con el divisor, forme un nuevo divisor para el nuevo dividendo. El nuevo número en el cociente tendrá el mismo número que el seleccionado en el divisor. La condición es la misma que sea menor o igual a la del dividendo.

Paso 5: Continúe este proceso hasta que obtengamos cero como resto. El cociente así obtenido será la raíz cuadrada del número.

Consideremos los siguientes ejemplos para comprender el método de división para determinar las raíces cuadradas.

Ejemplo 1: Encuentra la raíz cuadrada de 144 usando el método de división.

Solución:

Los pasos para determinar la raíz cuadrada de 144 son:

Paso 1: Comience la división desde el lado más a la izquierda. Aquí 1 es el número cuyo cuadrado es 1. 

Paso 2: ponerlo en el divisor y el cociente y luego duplicarlo dará como,

Paso 3: Ahora se requiere encontrar un número para los espacios en blanco en divisor y cociente. Sea ese número x. 

Paso 4: Por lo tanto, verifique cuando 2x multiplicado por x dé un número menor o igual a 44. Tome x = 1, 2, 3, etc. y verifique.

En este caso,

  • 21 × 1 = 21
  • 22 × 2 = 44

Así que elegimos x = 2 como el nuevo dígito a poner en el divisor y en el cociente. 

El resto aquí es 0 y por lo tanto 12 es la raíz cuadrada de 144.

Ejemplo 2: Encuentra la raíz cuadrada de 196 usando el método de división.

Solución:

Los pasos para determinar la raíz cuadrada de 196 son:

Paso 1: Comience la división desde el lado más a la izquierda. Aquí 1 es el número cuyo cuadrado es 1. 

Paso 2:  Ponerlo en el divisor y el cociente y luego duplicarlo dará.

Paso 3:  Ahora necesitamos encontrar un número para los espacios en blanco en el divisor y el cociente. Sea ese número x. 

Paso 4:  Necesitamos verificar cuando 2x multiplicado por x da un número menor o igual a 96. Toma x = 1, 2, 3 y así sucesivamente y verifica.

En este caso, 

  • 21 × 1 = 21
  • 22 × 2 = 44
  • 23 × 3 = 69
  • 24 × 4 = 96

Entonces, elige x = 4 como el nuevo dígito que se colocará en el divisor y en el cociente. 

El resto aquí es 0 y, por lo tanto, 14 es la raíz cuadrada de 196.

Ejemplo 2: Encuentra la raíz cuadrada de 225 usando el método de división.

Solución:

Los pasos para determinar la raíz cuadrada de 225 son:

Paso 1: Comience la división desde el lado más a la izquierda. Aquí 1 es el número cuyo cuadrado es 1. 

Paso 2:  Ponerlo en el divisor y el cociente y luego duplicarlo dará.

Paso 3:  Ahora necesitamos encontrar un número para los espacios en blanco en el divisor y el cociente. Sea ese número x. 

Paso 4:  Necesitamos verificar cuando 2x multiplicado por x da un número que es menor o igual a 125. Toma x = 1, 2, 3 y así sucesivamente y verifica.

En este caso,

  • 21 × 1 = 21
  • 22 × 2 = 44
  • 23 × 3 = 69
  • 24 × 4 = 96
  • 25 × 5 = 125

Así que elegimos x = 5 como el nuevo dígito para poner en el divisor y en el cociente. 

El resto aquí es 0 y por lo tanto 15 es la raíz cuadrada de 225.

4. Raíces cuadradas de números complejos 

Para calcular la raíz cuadrada de un número complejo, supongamos que la raíz es ea + ib. Luego compáralo con el número original para obtener los valores de a y b, obteniendo la raíz cuadrada.

Sea a + ib un número complejo, por lo tanto para encontrar la raíz cuadrada de a + ib se puede usar la siguiente fórmula

\sqrt{a+ib} = \pm(\sqrt{\frac{\sqrt{a^2+b^2}+a}{2}}+i\frac{b}{|b|}(\sqrt{\frac{\sqrt{a^2+b^2}-a}{2}}))

Consideremos los siguientes ejemplos para entender la determinación de las raíces cuadradas de números complejos.

Ejemplo 1: Encuentra la raíz cuadrada de 6 – 8i.

Solución:

Usemos la siguiente fórmula para determinar la raíz cuadrada del número complejo dado como:

\sqrt{a+ib} = \pm(\sqrt{\frac{\sqrt{a^2+b^2}+a}{2}}+i\frac{b}{|b|}(\sqrt{\frac{\sqrt{a^2+b^2}-a}{2}}))

Para el caso dado, sustituya a = 6 y b = (-8) en la fórmula anterior,

\begin{aligned}\sqrt{6-8i}&=\pm\sqrt{\dfrac{\sqrt{6^2+(-8)^2}+6}{2}}+i\dfrac{-8}{|-8|}\sqrt{\dfrac{\sqrt{6^2+(-8)^2}-6}{2}}\\&=\pm\sqrt{\dfrac{\sqrt{100}+6}{2}}-i\left(\dfrac{8}{8}\right)\sqrt{\dfrac{\sqrt{100}-6}{2}}\\&=\pm\sqrt{\dfrac{10+6}{2}}-i\sqrt{\dfrac{10-6}{2}}\\&=\pm\left(\sqrt{8}-i(\sqrt{2}\right)\\&=\pm(2\sqrt{2}-i\sqrt{2})\end{aligned}

cual es la solución requerida.

Ejemplo 2: Encuentra la raíz cuadrada de 9 + 40i.

Solución :

Usemos la siguiente fórmula para determinar la raíz cuadrada del número complejo dado como:

\sqrt{a+ib} = \pm(\sqrt{\frac{\sqrt{a^2+b^2}+a}{2}}+i\frac{b}{|b|}(\sqrt{\frac{\sqrt{a^2+b^2}-a}{2}}))

Para el caso dado, sustituya a = 9 y b = 40 en la fórmula anterior,

\begin{aligned}\sqrt{9+40i}&=\pm\left(\sqrt{\dfrac{\sqrt{9^2+{40}^2}+9}{2}}+i\dfrac{40}{|40|}\sqrt{\dfrac{\sqrt{9^2+(40)^2}-9}{2}}\right)\\&=\pm\left(\sqrt{\dfrac{\sqrt{81+{1600}}+9}{2}}+i\left(\dfrac{40}{40}\right)\sqrt{\dfrac{\sqrt{81+1600}-9}{2}}\right)\\&=\pm\left(\sqrt{\dfrac{\sqrt{1681}+9}{2}}+i\sqrt{\dfrac{\sqrt{1681}-9}{2}}\right)\\&=\pm\left(\sqrt{\dfrac{50}{2}}+i\sqrt{\dfrac{32}{2}}\right)\\&=\pm(5+4i)\end{aligned}

cual es la solución requerida.

Ejemplo 3: Encuentra la raíz cuadrada de 3 + 4i.

Solución :

Usemos la siguiente fórmula para determinar la raíz cuadrada del número complejo dado como:

\sqrt{a+ib} = \pm(\sqrt{\frac{\sqrt{a^2+b^2}+a}{2}}+i\frac{b}{|b|}(\sqrt{\frac{\sqrt{a^2+b^2}-a}{2}}))

Para el caso dado, sustituya a = 3 y b = 4 en la fórmula anterior,

\begin{aligned}\sqrt{3+4i}&=\pm\left(\sqrt{\dfrac{\sqrt{3^2+{4}^2}+3}{2}}+i\dfrac{4}{|4|}\sqrt{\dfrac{\sqrt{3^2+4^2}-3}{2}}\right)\\&=\pm\left(\sqrt{\dfrac{\sqrt{9+16}+3}{2}}+i\left(\dfrac{4}{4}\right)\sqrt{\dfrac{\sqrt{9+16}-3}{2}}\right)\\&=\pm\left(\sqrt{\dfrac{\sqrt{25}+3}{2}}+i\sqrt{\dfrac{\sqrt{25}-3}{2}}\right)\\&=\pm\left(\sqrt{\dfrac{5+3}{2}}+i\sqrt{\dfrac{5-3}{2}}\right)\\&=\pm(\sqrt{4}+i\sqrt{1})\\&=\pm(2+i)\end{aligned}

cual es la solución requerida.

Publicación traducida automáticamente

Artículo escrito por piyushkhandelwal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *