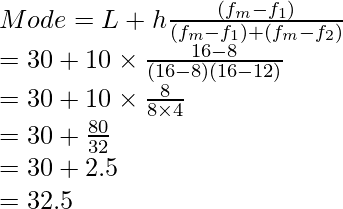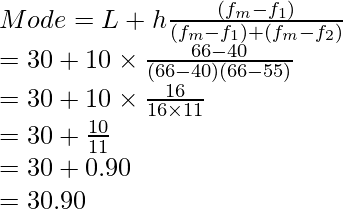En estadística, para una distribución de datos dada, la moda es el valor o número que ocurre con mayor frecuencia. Es representativo del valor o número entero que ocurre el número máximo de veces. Sin embargo, t, el
Fórmula para el modo
Aquí tenemos,
L – límite inferior de la clase modal,
h – tamaño del intervalo de clase,
fm – frecuencia de la clase modal,
f1 – frecuencia de la clase que precede a la clase modal, y
f2 – frecuencia de la clase que sucede a la clase modal.
Fórmula de moda de datos no agrupados
En el caso de datos no agrupados, la distribución de datos se organiza primero en orden ascendente o descendente. A continuación, los valores repetidos se representan junto con su frecuencia. La observación que corresponde a la frecuencia más alta se conoce como valor modal para los datos dados.
Fórmula de moda de datos agrupados
La fórmula de la moda para datos agrupados viene dada por,
Aquí tenemos,
L – límite inferior de la clase modal,
h – tamaño del intervalo de clase,
f m – frecuencia de la clase modal,
f 1 – frecuencia de la clase que precede a la clase modal y
f 2 – frecuencia de la clase que sucede a la clase modal.
¿Cómo encontrar el modo?
Modo para datos no agrupados
Los datos que no aparecen en grupos se conocen como datos no agrupados. Para ilustrar, tenemos un ejemplo en el que supongamos que hay una empresa de ropa que fabrica abrigos de invierno. Los siguientes datos tabulares con las camisetas junto con los tamaños se mencionan en la tabla de distribución de frecuencias que se muestra:
| Tamaño del abrigo de invierno. | 38 | 39 | 40 | 42 | 43 | 44 | 45 |
| Número total de camisetas | 33 | 11 | 22 | 55 | 44 | 11 | 22 |
Ya que, se evidencia que la talla 42 tiene la mayor frecuencia. Por lo tanto, la moda de la talla de los abrigos de invierno es 42.
El cálculo de la moda para datos no agrupados es diferente al de los datos agrupados.
Modo para datos agrupados
Los siguientes pasos corresponden al cálculo de la moda para datos agrupados:
Paso 1: Calcular el intervalo de clase que corresponde a la frecuencia máxima. Este valor también se denomina clase modal.
Paso 2: Calcule el tamaño de la clase restando el límite superior del límite inferior correspondiente.
Paso 3: Calcula el valor de la moda usando la fórmula de la moda:
![]()
¿Cómo encuentras la moda si no se repite ningún número?
Solución:
Para una distribución de datos que no tiene números repetidos, no existe moda. Para probar esto, supongamos una distribución de datos dada por: A, B, C, D y E.
Construyendo la tabla de distribución de frecuencias para el conjunto dado de observaciones, tenemos,
Observación A B C D mi Frecuencia 1 1 1 1 1 Podemos observar claramente que cada una de las observaciones se repite solo una vez, por lo que tiene una frecuencia equivalente a 1. Por lo tanto, no hay una ocurrencia máxima en este conjunto de datos y, por lo tanto, no hay moda.
Ejemplos de preguntas
Pregunta 1. Encuentra la moda de los datos desagrupados dados.
| color de la bicicleta | Rojo | Azul | Verde | Negro | Dorado | Plata | Gris |
| Número de coches vendidos | 15 | 25 | 42 | 32 | 35 | 55 | 22 |
Solución:
Aquí como para encontrar la moda de estos datos desagrupados
Observa el color de la bicicleta con la frecuencia más alta.
Como podemos ver, la bicicleta de color ‘Plata’ tiene la frecuencia más alta
Por lo tanto,
La moda es 55.
Pregunta 2. Calcular la moda de los datos agrupados que se dan a continuación
| Marcas obtenidas | Numero de estudiantes |
| 10-20 | 4 |
| 20-30 | 8 |
| 30-40 | dieciséis |
| 40-50 | 12 |
Solución:
Aquí tenemos que encontrar la moda de las marcas.
Primero encuentre la frecuencia máxima
f m = 16
El intervalo de clase correspondiente a f m es 30-40
El límite inferior de esta clase ‘L’ es 30
Tamaño del intervalo de clase = 10
Frecuencia de la clase precedente f 1 = 8
Frecuencia de la clase sucesiva f 2 = 12
Sustituye el valor en la fórmula de la moda
es decir,
Pregunta 3. Calcula la moda de los siguientes datos
15, 14, 19, 25, 26, 58, 109, 15, 14, 59, 58, 15, 17, 14, 19, 20, 25, 26, 109, 15, 109, 25, 59, 14, 17, 15
Solución:
Para encontrar la moda de los siguientes datos
Primero ordena los datos en orden ascendente
14, 14, 14, 14, 15, 15, 15, 15, 15, 17, 17, 19, 19, 20, 25, 25, 25, 26, 26, 58, 58, 59, 59, 109, 109, 109
Los números repetidos en los datos.
14 = 4 veces
15 = 5 veces
17 = 2 veces
19 = 2 veces
25 = 3 veces
26 = 2 veces
58 = 2 veces
59 = 2 veces
109 = 3 veces
Aquí como podemos ver que 15 ocurre la mayoría de las veces
Por lo tanto,
La moda de los datos es 15.
Pregunta 4. Encuentra la moda de la siguiente distribución de frecuencias
| Grupo de edad de los maestros en la escuela | 20-30 | 30-40 | 40-50 | 50-60 |
| Número de profesores | 40 | 66 | 55 | 20 |
Solución:
Frecuencia más alta f m = 66
Nivel inferior de frecuencia (L) = 30
Clase modal = 30-40
Frecuencia de la clase de intervalo que precede a f 1 = 40
Frecuencia de la clase que sucede a f 2 = 55
Ancho de la clase h = 10
De este modo,
Pregunta 5. Encuentra la moda de los datos
14, 15, 5, 3, 18, 19, 5, 16, 25, 33, 5, 3, 14, 18
Solución:
Para encontrar la moda primero ordena los datos en orden ascendente
3, 5, 5, 5, 14, 14, 15, 16, 18, 18, 19, 25, 33
Aquí como podemos observar que 5 está ocurriendo tiempos máximos
Por lo tanto,
La moda de los datos es 5.
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA