La seguridad del algoritmo RSA se basa en la dificultad de factorizar números muy grandes. La configuración de un criptosistema RSA implica la generación de dos números primos grandes, digamos p y q , a partir de los cuales se calcula el módulo RSA como n = p * q . Cuanto mayor sea el tamaño del módulo, mayor será el nivel de seguridad del sistema RSA. El tamaño de módulo RSA recomendado para la mayoría de las configuraciones es de 2048 bits a 4096 bits. Por lo tanto, los números primos que se generarán deben ser de 1024 bits a 2048.un poco largo Para la síntesis de números primos tan grandes, en lugar de depender de métodos deterministas, nos basamos en encontrar números que sean primos con un nivel de probabilidad satisfactoriamente alto.
Procedimiento de generación principal grande:
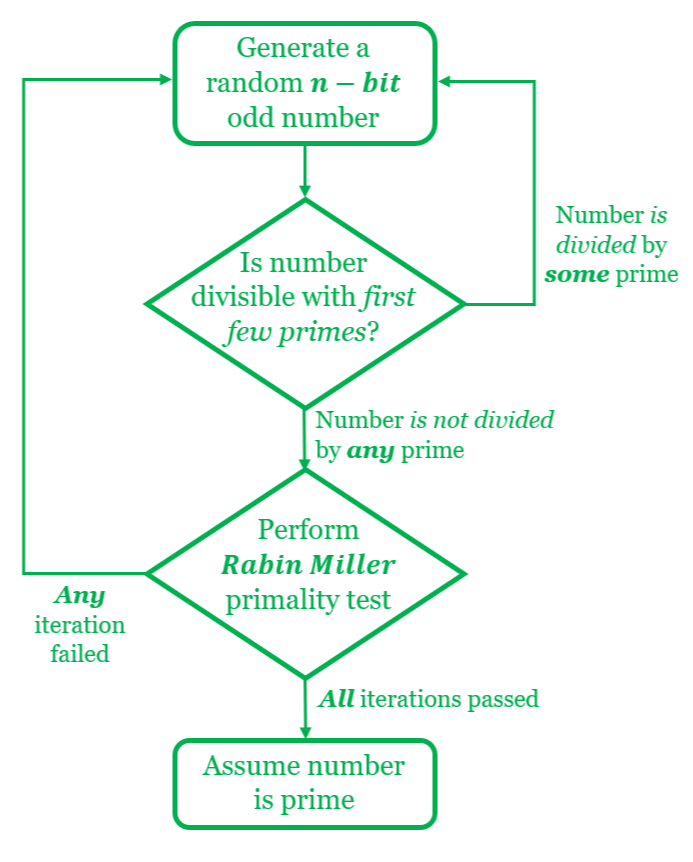
- El objetivo es calcular eficientemente números primos aleatorios muy grandes con un tamaño de bit específico. El método estándar de implementación manual de un generador de números primos aleatorios que puede generar valores primos con un nivel satisfactorio de precisión es el siguiente:
- Preseleccione un número aleatorio con el tamaño de bit deseado
- Asegúrese de que el número elegido no sea divisible por los primeros cientos de números primos (estos se generan previamente)
- Aplique un cierto número de iteraciones de la prueba de primalidad de Rabin Miller , según una tasa de error aceptable, para obtener un número que probablemente sea primo
A continuación se detallan los pasos para implementar el procedimiento anterior:
1. Elegir un candidato principal al azar
- La generación de un número aleatorio con n bits significa que el número aleatorio está en el rango 0 y
 . Algunas consideraciones a la hora de generar el número aleatorio son:
. Algunas consideraciones a la hora de generar el número aleatorio son:
- Debe evitarse la selección de números primos pequeños, como 3, 5, 7…, ya que la factorización del módulo RSA sería trivial. Por lo tanto, se debe tener cuidado de no tener demasiados ceros a la izquierda. Esto se puede hacer haciendo siempre el bit de mayor orden = 1
- Dado que todos los primos (> 2) son impares, para un mejor rendimiento, solo se puede elegir un número impar
- Por lo tanto, elegimos cualquier número aleatorio en el rango

Python3
def nBitRandom(n): # Returns a random number # between 2**(n-1)+1 and 2**n-1''' return(random.randrange(2**(n-1)+1, 2**n-1))
2. División con primeros números primos (prueba de primalidad de bajo nivel)
- Este paso es una prueba de primalidad de bajo nivel que requiere el cálculo previo de los primeros cientos de números primos (utilizando la criba de Eratóstenes ).
- El candidato principal se divide entre los números primos generados previamente para verificar la divisibilidad. Si el candidato principal es perfectamente divisible por cualquiera de estos números primos generados previamente, la prueba falla y se debe elegir y probar un nuevo candidato principal. Esto se repite siempre que se encuentre un valor que sea coprimo para todos los números primos en nuestra lista de números primos generados.
Python3
def getLowLevelPrime(n): '''Generate a prime candidate divisible by first primes''' # Repeat until a number satisfying # the test isn't found while True: # Obtain a random number prime_candidate = nBitRandom(n) for divisor in first_primes_list: if prime_candidate % divisor == 0 and divisor**2 <= prime_candidate: break # If no divisor found, return value else: return prime_candidate
3. Prueba de primalidad de Rabin Miller (prueba de primalidad de alto nivel)
- Un candidato principal que pasa la prueba de bajo nivel se prueba nuevamente usando la prueba de primalidad de Rabin Miller.
- Para números extremadamente grandes, como los que se usan en RSA, la prueba determinista de si el valor elegido es primo o no es muy poco práctica, ya que requiere una cantidad irrazonable de recursos informáticos.
- Se prefiere un enfoque probabilístico como tal. Si un valor ingresado pasa una sola iteración de la prueba de Rabin Miller, la probabilidad de que el número sea primo es del 75 % .
- Por lo tanto, un candidato que pasa la prueba, un número adecuado de veces, puede considerarse un número primo con un nivel de probabilidad satisfactorio.
- Por lo general, en aplicaciones comerciales, requerimos que las probabilidades de error sean menores a
 .
.
Python3
def isMillerRabinPassed(miller_rabin_candidate): '''Run 20 iterations of Rabin Miller Primality test''' maxDivisionsByTwo = 0 evenComponent = miller_rabin_candidate-1 while evenComponent % 2 == 0: evenComponent >>= 1 maxDivisionsByTwo += 1 assert(2**maxDivisionsByTwo * evenComponent == miller_rabin_candidate-1) def trialComposite(round_tester): if pow(round_tester, evenComponent, miller_rabin_candidate) == 1: return False for i in range(maxDivisionsByTwo): if pow(round_tester, 2**i * evenComponent, miller_rabin_candidate) == miller_rabin_candidate-1: return False return True # Set number of trials here numberOfRabinTrials = 20 for i in range(numberOfRabinTrials): round_tester = random.randrange(2, miller_rabin_candidate) if trialComposite(round_tester): return False return True
4. Combinando los pasos anteriores para generar el código
- Finalmente, podemos combinar las funciones anteriores para crear un proceso de tres pasos para generar números primos grandes. Los pasos serían
- Generación de números aleatorios llamando a nBitRandom( bitsize )
- Prueba de división básica llamando a getLowLevelPrime( prime_candidate )
- Prueba Rabin Miller llamando a isMillerRabinPassed( prime_candidate )
- Si el valor aleatorio elegido pasa todas las pruebas de primalidad, se devuelve como el número primo de n bits. De lo contrario, en caso de falla de la prueba, se selecciona un nuevo valor aleatorio y se prueba la primalidad. El proceso se repite hasta encontrar el número primo deseado.
A continuación se muestra la implementación completa del enfoque anterior.
Python3
# Large Prime Generation for RSA import random # Pre generated primes first_primes_list = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349] def nBitRandom(n): return random.randrange(2**(n-1)+1, 2**n - 1) def getLowLevelPrime(n): '''Generate a prime candidate divisible by first primes''' while True: # Obtain a random number pc = nBitRandom(n) # Test divisibility by pre-generated # primes for divisor in first_primes_list: if pc % divisor == 0 and divisor**2 <= pc: break else: return pc def isMillerRabinPassed(mrc): '''Run 20 iterations of Rabin Miller Primality test''' maxDivisionsByTwo = 0 ec = mrc-1 while ec % 2 == 0: ec >>= 1 maxDivisionsByTwo += 1 assert(2**maxDivisionsByTwo * ec == mrc-1) def trialComposite(round_tester): if pow(round_tester, ec, mrc) == 1: return False for i in range(maxDivisionsByTwo): if pow(round_tester, 2**i * ec, mrc) == mrc-1: return False return True # Set number of trials here numberOfRabinTrials = 20 for i in range(numberOfRabinTrials): round_tester = random.randrange(2, mrc) if trialComposite(round_tester): return False return True if __name__ == '__main__': while True: n = 1024 prime_candidate = getLowLevelPrime(n) if not isMillerRabinPassed(prime_candidate): continue else: print(n, "bit prime is: \n", prime_candidate) break
1024 bit prime is:
178542003245811211274167228297361192303886321036074276889145691522634525820185614278499562592134188995169731066418203258297035264969457638591284906658912408319763156912951486020761069099132619194489006875108217247513715271974383296142805846405783845170862140174184507256128825312324419293575432423822703857091
Nota: Generación de bibliotecas de números primos grandes en Python
La biblioteca pycrypto es una colección completa de funciones hash seguras y varios algoritmos de cifrado. También incluye funciones básicas comúnmente requeridas en las configuraciones de cifrado/descifrado, como la generación de números aleatorios y la generación de números primos aleatorios. El objetivo de generar un número primo aleatorio con un tamaño de bit específico se puede lograr utilizando el módulo pycrypto getPrime .
La sintaxis para generar un número primo aleatorio de n bits es:
Python3
from Crypto.Util import number number.getPrime(n)