¿Cómo hacer un ajuste de curvas exponencial y logarítmica en Python?

En este artículo, aprenderemos cómo hacer un ajuste de curva exponencial y logarítmico en Python. En primer lugar, surge la pregunta ¿Qué es el ajuste de curvas?

El ajuste de curvas es el proceso de construcción de una curva o función matemática, que tiene el mejor ajuste a una serie de puntos de datos, posiblemente sujeto a restricciones.

• Ajuste de curva logarítmica: La curva logarítmica es el gráfico de la función logarítmica.
• Ajuste de curva exponencial : La curva exponencial es el gráfico de la función exponencial.

Consideremos dos ecuaciones 

y = alog(x) + b donde a ,b  son coeficientes de esa ecuación logarítmica.

y = e ^(ax)*e(b)   donde a ,b  son coeficientes de esa ecuación exponencial.

Ajustaremos ambas curvas en la ecuación anterior y encontraremos la curva de mejor ajuste para ella. Para el ajuste de curvas en Python, usaremos algunas funciones de biblioteca

• entumecido
• matplotlib.pyplot

También usaríamos el método numpy.polyfit() para ajustar la curva. Esta función toma tres parámetros x, y y el grado del polinomio (n) devuelve los coeficientes del polinomio de grado n.

Sintaxis: numpy.polyfit(x, y, grados)

Parámetros:

• x ->x-coordenadas
• y ->y-coordenadas
• deg -> Grado del polinomio de ajuste. Entonces, si se le da uno a grados, obtenemos coeficientes de polinomio lineal o si es 2, obtenemos coeficientes de un polinomio cuadrático.

Ajuste de curva logarítmica

Para hacer el ajuste de la curva logarítmica, debemos seguir algunos pasos que se explican a continuación con la implementación.

Importación de bibliotecas

import numpy as np
  
# It is for ploting the curve
import matplotlib.pyplot as plt

Crear/Cargar datos

Como hemos importado las bibliotecas requeridas, tenemos que crear dos arrays llamadas x e y. Y después de crear esas dos arrays, tenemos que tomar el registro de los valores en x e y con la ayuda del método numpy.log().

# Points on X-axis
x_data = np.array([11, 23, 31, 43, 51]) 
  
# Points on Y-axis
y_data = np.array([2, 4, 6, 8, 10])     
  
print(x_data)
print(y_data)
  
# Taking log of x values
xlog_data = np.log(x_data)             
  
print(xlog_data)

Producción:

Ajuste de datos

Después de obtener los valores logarítmicos de las arrays x e y, con la ayuda de numpy.polyfit() encontramos el coeficiente para nuestra ecuación. Como tomamos una ecuación lineal, por lo tanto, en el método polyfit, pasaremos 1 en el parámetro de grado.

# Given log values of x , y as input
curve = np.polyfit(log_x_data, y_data, 1)
  
print(curve)

Producción:

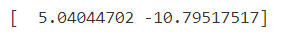
Obtener salida

Entonces obtenemos los coeficientes como [5.04, -10.79] con eso podemos obtener la ecuación de la curva que sería (y= a*log(x)+y, donde a,b son coeficiente)

y = 5.04*log(x) - 10.79

y = 5.04 * log_x_data - 10.79  
  
print(y)

Producción:

Trazado de resultados

Ahora, tracemos los gráficos uno con xlog_data, ylog_data y otro con xlog_data y la ecuación y que hemos obtenido. Para trazar gráficos en python, tomaremos la ayuda de la función Matplotlib.pyplot.plot() .

Sintaxis: matplotlib.pyplot.plot(coordenadas x, coordenadas y)

Parámetros:

• x: coordenadas horizontales de los puntos de datos
• y: coordenadas verticales de los puntos de datos

# Blue color
plt.plot(log_x_data, y_data)
  
# Best fit in orange
plt.plot(log_x_data, y)

Producción:

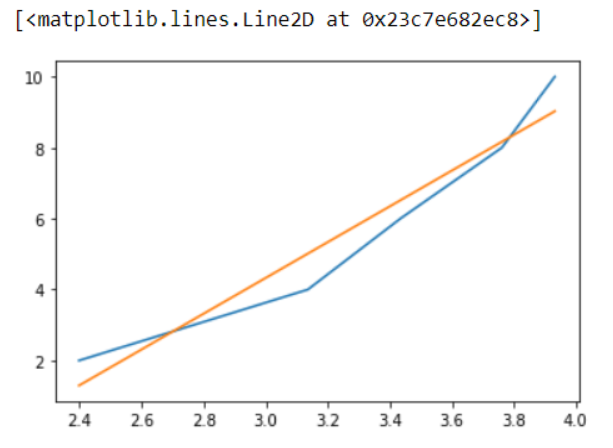
En el gráfico anterior, la línea amarilla representa el gráfico de las coordenadas x e y originales y la línea azul es el gráfico de coordenadas que hemos obtenido a través de nuestros cálculos, y es el que mejor se ajusta.

Ajuste de curva exponencial

Repetiremos el mismo proceso anterior, pero la única diferencia es que la función logarítmica se reemplaza por la función exponencial.

Primero, vamos a crear los puntos de datos

x_data = np.array([11, 19, 31, 39, 51])
print(x_data)
  
y_data = np.array([5, 8, 32, 84, 110])
print(y_data)

Producción:

Equation: y = e(ax)*e(b)

En esta ecuación trazaremos el gráfico y a, b son coeficientes que podemos obtener con el método numpy.polyfit(). Ahora vamos a encontrar los coeficientes de la función exponencial con grado .

ylog_data = np.log(y_data)
print(ylog_data)
  
curve_fit = np.polyfit(x_data, log_y_data, 1)
print(curve_fit)

Producción:

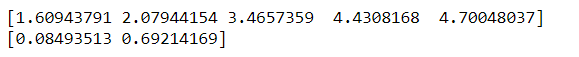
Entonces, a = 0.69 y b = 0.085 estos son los coeficientes podemos obtener la ecuación de la curva que sería (y = e ^(ax) *e ^(b), donde a, b son coeficiente)

y = e(0.69x)*e(0.085) final equation.

y = np.exp(0.69) * np.exp(0.085*x_data)
  
print(y)

Producción:

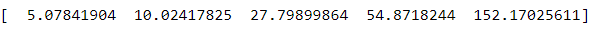
Ahora, tracemos los gráficos con la ayuda de la función Matplotlib.pyplot.plot() .

# Blue 
plt.plot(x_data, y_data)
  
# best fit in orange
plt.plot(x_data, y)

Producción:

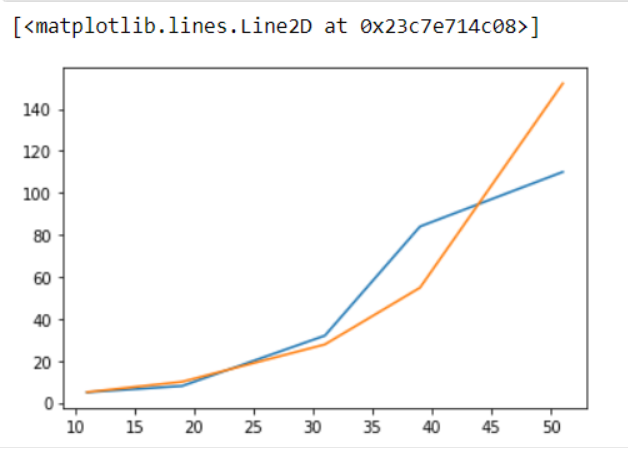
En el gráfico anterior, la línea azul representa el gráfico de las coordenadas x e y originales y la línea naranja es el gráfico de coordenadas que hemos obtenido a través de nuestros cálculos, y es el que mejor se ajusta.

Por lo tanto, este es el proceso de ajuste de curvas exponenciales y logarítmicas en Python con la ayuda de NumPy y matplotlib.