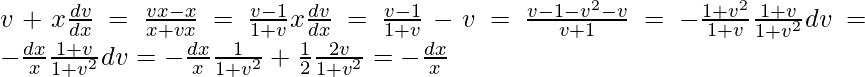¿Cómo resolver ecuaciones diferenciales?

Las ecuaciones que tienen una variable independiente, así como la variable dependiente y la derivada de la variable dependiente con respecto a la variable independiente, se conocen como ecuaciones diferenciales. Aquellas ecuaciones diferenciales que contienen una sola variable independiente se denominan ecuaciones diferenciales ordinarias y las que tienen más de una variable independiente y su derivada parcial se denominan ecuaciones diferenciales parciales.

$\frac{dy}{dx} + x = 0.$ In this equation, X is the independent variable and Y is the dependent variable of x, where derivative of dependent one with independent variable X.

Formas de ecuaciones diferenciales

xdy + ydx = 0
$\frac{d^2y}{dx^2} + 4y = 0$
$y = x\frac{dy}{dx } + \frac{a}{\frac{dy}{dx}}$
$\frac{dy}{dx} + cos(\frac{dy}{dx}) = 0$

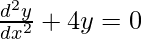
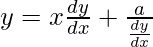
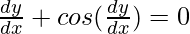
Resolviendo ecuaciones diferenciales

Hay diferentes formas de resolver ecuaciones diferenciales. Son los métodos de separación de variables, ecuaciones diferenciales homogéneas, ecuaciones diferenciales lineales, etc. Aprendamos cada uno de los métodos en detalle,

Por método de separación variable

En la ecuación, si es posible obtener todas las mismas funciones en un lado, la función media de x y dx en un lado es igual para y y dy en el otro lado, entonces podemos decir separación de una variable.

Tipo 1

Sea $\frac{dy}{dx}$ = f(x)

Ahora separe todas las funciones de x y dx en un lado,

dy = f(x)dx

Ahora, integrando ambos lados,

∫dy =∫f(x)dx

y = ∫f(x)

Cuál es la solución requerida, donde c es una constante arbitraria.

Tipo 2

$\frac{dy}{dx} = f(x)g(x)$

Separe las mismas funciones en un lado,

$\int\frac{dy}{g(y)} =\int{f(x) dx} +c$

Donde c es una constante arbitraria.

Por ecuaciones diferenciales homogéneas

Una ecuación diferencial en x e y se dice que es una ecuación homogénea si se puede poner en forma de $\frac{dy}{dx} = \frac{f_1(x,y)}{f_2(x,y)}$ , donde f ₁ (x, y) y f ₂ (x, y) son del mismo grado en x e y. Por lo tanto, ambas funciones son homogéneas en grados de x e y.

Para resolver ecuaciones diferenciales,

Ponga y = vx.
Después $\frac{dy}{dx} = v + x\frac{dv}{dx}$
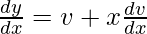
Separe las variables vyx, e integre.
Sustituye v de y = vx.

Se obtuvo la solución requerida.

Por ecuaciones diferenciales lineales

Se dice que una ecuación diferencial es lineal si la variable dependiente y sus coeficientes diferenciales ocurren solo en primer grado y no se multiplican entre sí.

$\frac{dy}{dx} + Py=Q$ , where P and Q are constants or functions of x only, is called a differential equation of first order. Similarly, $\frac{dx}{dy}+Px =Q$ , where P and Q are constants or functions of y only, is called a linear differential equation of first order.

regla de trabajo

Sea ecuación diferencial lineal $\frac{dy}{dx}$ + Py = Q

Identificar la P y la Q de las ecuaciones dadas
Encuentre el factor de integración (IF), es decir, e ^∫pdx
La solución viene dada por y(SI) =∫ Q(SI)dx + c

Caso especial: Ecuación de Bernoulli

Una ecuación de la forma $\frac{dy}{dx} +Py = Qyn,$ en que P y Q son funciones de x únicamente y n ≠ 0, 1 se conoce como ecuación diferencial de Bernoulli. Es fácil reducir la ecuación a la forma lineal como se muestra a continuación dividiendo ambos lados por y _n ,

y – n $\frac{dy}{dx}$ + Py ^{1 – n} = Q

sea y ^{1 – n} = z

z = (1 – n)y ^-n $\frac{dy}{dx} = \frac{dz}{dx}$

La ecuación dada se convierte en $\frac{dz}{dx}$ + (1 – n)Q

Que son ecuaciones lineales en z.

Aquí, Si = e∫ ^(1-n)P dx

La solución requerida es,

z(SI) = ∫(1 – n) Q e ^{∫(1 – n)Pdx}

Problemas de muestra

Problema 1: Resolver la ecuación diferencial $\frac{dy}{dx} = \frac{y-x}{x+y}$

Solución:

$\frac{dy}{dx} = \frac{y-x}{x+y}$ ⇢ (1)

Que es una ecuación diferencial homogénea como función y – x y x + y es de grado 1.

Ponga y = vx ⇢ (2)

Derivamos la ecuación (2), obtenemos

$\frac{dy}{dx} = v+x\frac{dv}{dx}$ ⇢ (3)

De la ec. (3) a la ecuación. (1), tenemos

$v+x\frac{dv}{dx} = \frac{vx-x}{x+vx} = \frac{v-1}{1+v} x\frac{dv}{dx} =\frac{v-1}{1+v} -v = \frac{v-1-v^2-v}{v+1} = -\frac{1+v^2}{1+v} \frac{1+v}{1+v^2} dv=-\frac{dx}{x} ∫ \frac{1+v}{1+v^2} dv=-∫\frac{dx}{x} ∫\frac{1}{1+v^2} + \frac{1}{2} ∫\frac{2v}{1+v^2} =- ∫\frac{dx}{x}$

Después de una clasificación adicional, obtenemos

$tan^-1\frac{y}{x} + log(x^2+y^2) =c$

Problema 2: Resuelve $(x tan \frac{y}{x}-ysec^2 \frac{y}{x})dx-xsec^{2} \frac{y}{x}dy=0$

Solución:

$(x tan \frac{y}{x}-ysec^2 \frac{y}{x})dx-xsec^2 \frac{y}{x}dy=0$ ⇢ (1)

Después de derivar, podemos escribir las ecuaciones anteriores como,

$\frac{dy}{dx} = (\frac{y}{x}sec^2\frac{y}{x}-tan\frac{y}{x})cos^2\frac{y}{x}$

Las ecuaciones anteriores son homogéneas. Poniendo y = vx

$v+x\frac{dv}{dx}=(vsec^2v-tanv)cos^2v$

x dv/dx = v – tanv cos ² v – v

Separando las variables $\frac{sec^2v}{tanv}dv=-dx/x$

Integrando ambos lados log tanv = -logx + logc

xtanv = C

De y = vx, obtenemos

xtanía/x = C

Problema 3: Resolver la ecuación diferencial $\frac{dy}{dx}$ +y = senx

Solución:

$\frac{dy}{dx}$ + y = senx (Dado)

Al compararlo con $\frac{dy}{dx}$ + Py = Q, obtenemos: p = 1 y Q = senx

SI =∫ e ^(pdx) = e ^x

Como sabemos, y(SI) = ∫Q(SI)dx + c

ye ^x = ∫ senx e ^x

Después de la integración obtenemos

tu ^x = $\frac{e^x}{2} (sinx-cosx) +c$

y = 1/2 (senx-cosx) + c

Problema 4: Resuelve, $x(\frac{dy}{dx}) + y =y^{2logx}$

Solución:

La ecuación dada se puede escribir como,

$\frac{dy}{dx}+\frac{y}{x} = \frac{y^2}{x}logx$ (Dividiendo por x)

$\frac{dy}{dx}+\frac{y}{x}=\frac{y^2}{x}logx$

Ahora, divide el pensamiento y ²

$\frac{dy}{dx}\frac{1}{y^2}+\frac{1}{xy}=\frac{logx}{x}$ ⇢ (A)

Ponga 1/y = v ⇢ (1)

Después de derivar la ecuación (1), obtenemos

$(\frac{-1}{y^2})\frac{dy}{dx}=(\frac{dv}{dx})$

Por ecuación de sustitución (A)

$\frac{dv}{dx}-\frac{v}{x}=-\frac{logx}{x}$

Esto es lineal con v como las variables dependientes.

Aquí, P= $-\frac{1}{x}$ , Q= $-\frac{logx}{x}$

SI = e ^∫Pdx =e ^∫(-1/x)dx =e ^-logx 1/x

Por eso,

1/xy = (1\x)logx + 1\x + C

Problema 5 : Resuelva la ecuación diferencial: $\frac{dy}{dx} = (e^x + 1)y$

Solución:

dy/dx = (e ^x + 1)y ⇢ (dado)

dy/y = (ex ⁺ 1) dx

Integrando ambos lados,

∫dy/y = ∫(e ^x + 1) dx

log|y| =e ^x + x + c

Problema 6 : Resuelva las siguientes ecuaciones diferenciales,

dy/y = ytan2x
dy/dx = (1 + x ² )(1 + y ² )

Solución:

dy/y = ytan2x ⇢ (dado)

∫1/ydy = tan2x . dx ⇢ (separando variables)

Integrando ambos lados,

∫1/ydy = ∫tan2x dx

log|y| = 1/2log|seg2x| +c

$\frac{dy}{dx}$ = (1 + x ² )(1 + y ² ) ⇢ (dado)

Integrando ambos lados, obtenemos;

$∫\frac{dy}{1+y^2}$ = ∫(1 + x ² )dx

tan ^-1 y = x + x ³ /3 + c,

Publicación traducida automáticamente

Artículo escrito por uditsharma333jj y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Resolviendo ecuaciones diferenciales

Problemas de muestra

Deja una respuesta Cancelar la respuesta