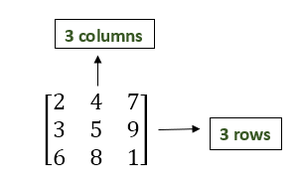
¿Cómo Resolver un Sistema de Ecuaciones usando Inverso de Arrays?

En matemáticas, una array es un conjunto de números dispuestos en un patrón rectangular y separados en filas y columnas. Por lo general, se representan encerrando todos los números enteros entre corchetes.

Determinante

El determinante de una array es el valor escalar producido para una array cuadrada dada. El determinante se trata en álgebra lineal y se calcula usando los elementos de una array cuadrada. Un determinante es un valor escalar o número calculado usando una array cuadrada. La array cuadrada puede ser 2 × 2, 3 × 3, 4 × 4 o cualquier otra forma en la que el número de columnas y filas sea igual, como n × n. Si S es el conjunto de arrays cuadradas, R es el conjunto de enteros (reales o complejos), y f: S → R está definida por f (A) = k, donde A ∈ S y k ∈ R, entonces f (A ) se conoce como determinante de A. Un determinante se representa mediante dos líneas verticales, es decir, |A|.

Determinante de la array 2×2 –

$\left[\begin{matrix}a&b\\c&d\\\end{matrix}\right] = a ×d - b ×c$

Determinante de la array 3×3 – $\left[\begin{array}a&b&c\\d&e&f\\g&h&i\\\end{array}\right]=a(ei-fh)-b(di-gf)+c(dh-ge)$

Menores y Cofactores

La array creada después de eliminar la fila y la columna de la array en la que se encuentra ese elemento específico se define como el menor de la array.

El menor del elemento a ₁₂ es M ₁₂ – $\left[\begin{array}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\ \end{array}\right]=\left[\begin{array}a_{21}&a_{23}\\a_{31}&a_{33}\\\end{array}\right]$

El cofactor de un elemento en la array A se obtiene multiplicando el menor M _ij del elemento por (-1) ^i+j . C _ij es el símbolo del cofactor de un elemento. Si el menor de una array es M _ij , entonces el cofactor del elemento sería: C _{ij =} (-1) ^i+j M _{ij .}La array de cofactores es la array creada por los cofactores de los componentes de la array.

Array de cofactores: $\left[\begin{array}C_{11}&C_{12}&C_{13}\\C_{21}&C_{22}&C_{23}\\C_{31}&C_{32}&C_{33}\\ \end{array}\right]$

Adjunto de una array

Sea A=[aij] una array cuadrada de n dimensiones. El adjunto de una array A es la transpuesta de la array cofactor de A. Está simbolizado por la letra adj A. Las arrays adjuntas a veces se conocen como arrays adjuntas. El adjunto de una array cuadrada A = [aij]nxn se define como la transpuesta de la array [Aij]nxn, donde Aij es el cofactor del elemento aij.

$Let A = \left[\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right]$

Adjunto de A=Transpuesta de $\left[\begin{matrix}A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}\\\end{matrix}\right]$ = $\left[\begin{matrix}A_{11}&A_{21}&A_{31}\\A_{12}&A_{22}&A_{32}\\A_{13}&A_{23}&A_{33}\\\end{matrix}\right]$

La inversa de una array

Una array cuadrada A es invertible si y solo si A es una array no singular. La inversa de una array se puede obtener dividiendo el adjunto de una array por el determinante de la array. La inversa de una array se puede calcular siguiendo los pasos a continuación:

Paso 1: Determinar el menor de la array proporcionada.
Paso 2: Convertir la array adquirida en la array de cofactores.
Paso 3: Finalmente, el adyuvante, y
Paso 4: Multiplícalo por el recíproco del determinante.

Sea A= $\left[\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right]$

Inversa de la array A = A ^{-1} = $\frac{1}{|A|} \left[\begin{matrix}A_{11}&A_{21}&A_{31}\\A_{12}&A_{22}&A_{32}\\A_{13}&A_{23}&A_{33}\\\end{matrix}\right]$

Aplicación de Arrays y Determinantes

Ahora, veamos cómo se pueden usar los determinantes y las arrays para resolver sistemas de ecuaciones lineales en dos o tres variables y para evaluar la consistencia del sistema.

Sistema consistente : un sistema de ecuaciones se considera consistente si tiene (una o más) soluciones.
Sistema Inconsistente : Si la solución a un sistema de ecuaciones no existe, se dice que el sistema es inconsistente.

Representación de sistemas lineales con ecuaciones matriciales

Se puede utilizar una array aumentada para representar un sistema de ecuaciones. Cada fila en una array aumentada representa una de las ecuaciones del sistema, mientras que cada columna representa una variable o los términos constantes. Podemos ver que las arrays aumentadas son un atajo para formular sistemas de ecuaciones de esta manera.

Ejemplo: Escriba el siguiente sistema de ecuaciones como una array aumentada.

x-2y = 5

4x – 3y – z = 3

5y – 7z = 9

Escribamos la siguiente array en forma aumentada. Si no se da un término variable en la array, se considera que el coeficiente de ese término es ‘ 0 ‘.

(1)x + (-2)y + (0)z = 5

(4)x + (-3)y + (-1)z = 3

(0)x + (5)y + (-7)z = 9

La siguiente array aumentada es: $\left[\begin{matrix}1&-2&0&5\\4&-3&-1&3\\0&5&-7&9\\\end{matrix}\right]$

Resolver sistemas lineales con ecuaciones matriciales

La resolución de ecuaciones lineales utilizando una array se realiza mediante el método Matrix. En este artículo, veremos cómo resolver ecuaciones lineales con ejemplos de arrays.

Resolver ecuaciones con arrays inversas

Supongamos que la ecuación es: 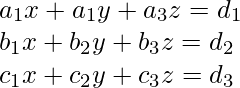$a_1x+a_1y+a_3z=d_1 \\b_1x+b_2y+b_3z=d_2\\ c_1x+c_2y+c_3z=d_3$

El método matricial se utiliza para encontrar la solución del sistema de ecuaciones. En las ecuaciones, todas las variables deben escribirse en el orden correcto. En los lados apropiados, escribe las variables, sus coeficientes y constantes.

El método de determinación de la inversa se utiliza para resolver un sistema de ecuaciones lineales y requiere dos arrays adicionales. Las variables están representadas por la Array X. Las constantes están representadas por la Array B. Usando la multiplicación de arrays, un sistema de ecuaciones con el mismo número de ecuaciones que una variable se define como,

AX=B

Sea A la array de coeficientes, X la array variable y B la array constante para resolver un sistema de ecuaciones lineales con array inversa. Como resultado, nos gustaría resolver el sistema AX = B. Eche un vistazo a las siguientes ecuaciones como ejemplo.

$\left[\begin{matrix}a_1x+a_2y+a_3z\\b_1x+b_2y+b_3z\\c_1x+c_2y+c_3z\\\end{matrix}\right]=\left[\begin{matrix}d_1\\d_2\\d_3\\\end{matrix}\right]$

$\left[\begin{matrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\\\end{matrix}\right]\left[\begin{matrix}x\\y\\z\\\end{matrix}\right]=\left[\begin{matrix}d_1\\d_2\\d_3\\\end{matrix}\right]$

AX = B

dónde: $A=\left[\begin{matrix}a_1&a_2&a_3\\b_1&b_2&b_3\\c_1&c_2&c_3\\\end{matrix}\right],X=\left[\begin{matrix}x\\y\\z\\\end{matrix}\right],B=\left[\begin{matrix}d_1\\d_2\\d_3\\\end{matrix}\right]$

Caso 1: Si A es una array no singular, tiene inversa.

Sea A la array de coeficientes, X la array variable y B la array constante para resolver un sistema de ecuaciones lineales con array inversa. Como resultado, nos gustaría resolver el sistema AX=B. Para obtener la respuesta, multiplica ambos lados por el inverso de A.

$(A^{-1})AX=(A^{-1})B [(A^{-1})A]X=(A^{-1})B IX=(A^{-1})B X=(A^{-1})B$

Como la inversa de una array es única, esta ecuación matricial ofrece una solución única al sistema de ecuaciones dado. El Método Matrix es un método para resolver sistemas de ecuaciones.

Caso 2: Si A es una array singular, entonces | A| = 0. En este caso, calcule (adj A) B.

Si (adj A) B ≠ O, (siendo O arrays cero), entonces la solución no existe y el sistema de ecuaciones se llama inconsistente.

Si (adj A) B = O, entonces el sistema puede ser consistente o inconsistente, ya que el sistema tiene infinitas soluciones o ninguna solución.

Problemas de muestra

Pregunta 1: Encuentra lo siguiente de la array dada $A=\left[\begin{matrix}3&2&-1\\-5&0&-2\\3&4&-1\\\end{matrix}\right]$

determinante de la array A
array de cofactores A
adjunto de la array A
inversa de la array A

Solución:

La array dada es $A=\left[\begin{matrix}3&2&-1\\-5&0&-2\\3&4&-1\\\end{matrix}\right]$

Determinante de la A = $3(0\times (-1) - 4\times(-2))+5(2\times(-1)-4\times(-1))+3(2\times(-2)-0\times (-1))$

= 3(0+8)+5(-2+4)+3(-4)

= 3 × 8 + 5 × 2 + 3 × (-4)

= 24 + 10 – 12 unidades

Cofactor de la array A =

C

C

Array de cofactores de A = $C=\left[\begin{matrix}8&-11&-20\\-2&0&-6\\-4&11&10\\\end{matrix}\right]$

AdjoinT de la array A = transpuesta de la array cofactor C = $C=\left[\begin{matrix}8&-11&-20\\-2&0&-6\\-4&11&10\\\end{matrix}\right]^{'}$

$C=\left[\begin{matrix}8&-2&-4\\-11&0&11\\-20&-6&10\\\end{matrix}\right]$

Inversa de la array A = $A^{-1}=\frac{1}{|A|}adj.A$

= $\frac{1}{22} \left[\begin{matrix}8&-2&-4\\-11&0&11\\-20&-6&10\\\end{matrix}\right]$

= $\left[\begin{matrix}\frac{4}{11}&\frac{-1}{11}&\frac{-2}{11}\\\frac{-1}{2}&0&\frac{1}{2}\\\frac{-10}{11}&\frac{-3}{11}&\frac{5}{11}\\\end{matrix}\right]$

Pregunta 2: Ram es contratado para un trabajo con un pago mensual de una cantidad específica y un aumento anual de una cantidad predeterminada. Calcule su salario inicial y el aumento anual si su salario era de $300 por mes al final del primer mes después de 1 año de servicio y $600 por mes al final del primer mes después de 3 años de servicio.

Solución:

Sean “x” e “y” el salario mensual y un aumento anual de cierta cantidad, respectivamente.

Según la pregunta;

x + y = 300 ⇢ (yo)

x + 3y = 600 ⇢ (ii)

Esto se puede escribir como AX = B, donde

$A=\left[\begin{matrix}1&1\\1&3\\\end{matrix}\right],X=\left[\begin{matrix}x\\y\\\end{matrix}\right] ,B=\left[\begin{matrix}300\\600\\\end{matrix}\right]$

Determinante de A =

Adjunto de A = $\left[\begin{matrix}3&-1\\-1&1\\\end{matrix}\right]$

De este modo, $A^{-1}=\frac{1}{|A|}adj.A$

$A^{-1}=\frac{1}{2}\left[\begin{matrix}3&-1\\-1&1\\\end{matrix}\right]$

Usando array inversa,

X = A ^-1B

$X= \frac{1}{2} \left[\begin{matrix}3&-1\\-1&1\\\end{matrix}\right]\left[\begin{matrix}300\\600\\\end{matrix}\right]$

$X=\frac{1}{2} \left[\begin{matrix}3\times300+(-1)\times600\\(-1)\times300+1\times600\\\end{matrix}\right]$

$X= \frac{1}{2} \left[\begin{matrix}300\\300\\\end{matrix}\right]$

$X=\left[\begin{matrix}150\\150\\\end{matrix}\right]$

Por lo tanto; x = $150, y = $150

Entonces, el salario mensual es de $150 y el incremento anual es de $150.

Pregunta 3: La suma de tres números es 3. Si multiplicamos el segundo número por 2 y le sumamos el primer número, obtenemos 6. Si multiplicamos el tercer número por 4 y le sumamos el segundo, obtenemos 10 Representarla algebraicamente y hallar los números por el método matricial.

Solución:

Sean x, y y z los números primero, segundo y tercero, respectivamente. Entonces, de acuerdo con la pregunta, tenemos

x + y + z = 3

x + 2y = 6

y + 4z = 10

Esto se puede escribir como AX = B, donde $A=\left[\begin{matrix}1&1&1\\1&2&0\\0&1&4\\\end{matrix}\right],X=\left[\begin{matrix}x\\y\\z\\\end{matrix}\right] ,B=\left[\begin{matrix}3\\10\\6\\\end{matrix}\right]$

Aquí, |A|= 1(8 – 0) – 1(4 – 0) + 1(1 – 0) = 8 – 4 + 1 = 5 ≠ 0. Ahora, encuentra adj A.

UN ₁₁ = 8 – 0 = 8, UN ₁₂ = -(4 – 0) = -4, UN ₁₃ = 1 – 0 = 1

A ₂₁ = -(4 – 1) = -3, A ₂₂ = 4 – 0 = 4, A ₂₃ = -(1 – 0) = -1

A ₃₁ = 0 – 2 = -2, A ₃₂ = -(0 – 1) = 1, A ₃₃ = 2 – 1 = 1

adj. un = $\left[\begin{matrix}8&-3&-2\\-4&4&1\\1&-1&1\\\end{matrix}\right]$

De este modo, $A^{-1}=\frac{1}{|A|}Adj. of A=\frac{1}{5}\left[\begin{matrix}8&-3&-2\\-4&4&1\\1&-1&1\\\end{matrix}\right]$

X = A ^-1B

$X=\frac{1}{5}\left[\begin{matrix}8&-3&-2\\-4&4&1\\1&-1&1\\\end{matrix}\right]\left[\begin{matrix}3\\10\\6\\\end{matrix}\right]$

$\left[\begin{matrix}x\\y\\z\\\end{matrix}\right]=\frac{1}{5}\left[\begin{matrix}24-30-12\\-12+40+6\\3-10+6\\\end{matrix}\right]=\frac{1}{5}\left[\begin{matrix}-18\\34\\-1\\\end{matrix}\right]=\left[\begin{matrix}\frac{-18}{5}\\\frac{34}{5}\\\frac{-1}{5}\\\end{matrix}\right]$

Por lo tanto;

$X=\frac{-18}{5}, Y= \frac{34}{5}, Z=\frac{-1}{5}$

Pregunta 4: Supongamos que Joe, Max y Polly fueron de compras al centro comercial. Joe paga 45/- por 4 kg de manzanas, 7 kg de bananas y 6 kg de guayabas, Max paga 30/- por 2 kg de manzanas y 5 kg de guayabas, y Polly paga 35/- por 3 kg de manzanas. 1 kg de plátanos y 4 kg de guayabas. ¿Cuánto cuestan las manzanas, los plátanos y las guayabas por kilogramo?

Solución:

Sean x, y y z las cantidades de manzanas, bananas y guayabas, respectivamente.

De acuerdo a la pregunta:

4x + 7y + 6z = 45

2 x + 5 z = 30

3x + y + 4z = 35

La array A contiene los kg de manzanas, plátanos y guayabas que compraron Joe, Max y Polly. La array B contiene los precios pagados por los tres y la array X contiene las variables.

$A=\left[\begin{matrix}4&7&6\\2&0&5\\3&1&4\\\end{matrix}\right],X=\left[\begin{matrix}x\\y\\z\\\end{matrix}\right] ,B=\left[\begin{matrix}45\\30\\35\\\end{matrix}\right]$

La solución del sistema de ecuaciones dado sea X = A ^-1 B.

Para encontrar el inverso de A, primero encontraremos el determinante de A.

$A=\left[\begin{matrix}4&7&6\\2&0&5\\3&1&4\\\end{matrix}\right],X=\left[\begin{matrix}x\\y\\z\\\end{matrix}\right] ,B=\left[\begin{matrix}45\\30\\35\\\end{matrix}\right]$

$A^{-1}=\frac{1}{|A|}adj. A$

Determinante de A = |A| = 4(0 × 4 – 1 × 5) – 7(2 × 4 – 5 × 3) + 6(2 × 1 – 3 × 0)

= 4(0 – 5) – 7(8 – 15) + 6(2 – 0)

= -20 – 7(-7) + 12

= -20 + 49 + 12 = 41

adj. de A = $\left[\begin{matrix}-5&-22&35\\7&-2&-6\\2&17&-14\\\end{matrix}\right]$

$A^{-1}=\frac{1}{41}adj.A$

$X=A^{-1}B=\frac{1}{41}\left[\begin{matrix}-5&-22&35\\7&-2&-6\\2&17&-14\\\end{matrix}\right]\times \left[\begin{matrix}45\\30\\35\\\end{matrix}\right]$

$X=\frac{1}{41}\left[\begin{matrix}340\\45\\110\\\end{matrix}\right]=\left[\begin{matrix}8.3\\1.1\\2.7\\\end{matrix}\right]$

El costo de las manzanas por kg = 8.3/-

El costo de los bananos por kg = 1.1/-

El costo de las guayabas por kg = 2.7/-

Pregunta 5: El costo de 2 kg papas, 3 kg tomates y 2 kg harina es 50. El costo de 5 kg papas, 1 kg tomates y 6 kg harina es 40. El costo de 4 kg papas, 6 kg tomates y 3 kg kg de harina es 60. Encuentra el costo de cada artículo por kg por el inverso de una array.

Solución:

Sean x, y y z los kg de patatas, tomates y harina, respectivamente.

De acuerdo a la pregunta:

2x + 3y + 2z = 50

5x + 1y + 6z = 40

4x + 6y + 3z = 60

La array A contiene los kg de patatas, tomates y harina. La array B contiene los precios pagados y la array X contiene las variables. Esto se puede escribir como AX = B, donde $A=\left[\begin{matrix}2&3&2\\5&1&6\\4&6&3\\\end{matrix}\right],X=\left[\begin{matrix}x\\y\\z\\\end{matrix}\right] ,B=\left[\begin{matrix}50\\40\\60\\\end{matrix}\right]$

La solución del sistema de ecuaciones dado es X = A ^-1 B. Para encontrar el inverso de A, primero encontraremos el determinante de A.

Determinante de A |A| = 2(3 – 36) – 3(15 – 24) + 2(30 – 4) = 2 × (-33) – 3(-9) + 2(26) = -66 + 27 + 52 = 13

Ahora, encuentre el adjunto de A para obtener el inverso de A.

UN ₁₁ = 3 – 36 = -33, UN ₁₂ = -(15 – 24) = 9, UN ₁₃ = 30 – 4 = 26

A ₂₁ = -(9 – 12) = 3, A ₂₂ = 6 – 8 = -2, A ₂₃ = -(12 – 12) = 0

un ^{-1} = $A^{-1}=\frac{1}{|A|}adj.A=\frac{1}{13}\left[\begin{matrix}-33&3&16\\9&-2&-2\\26&0&-13\\\end{matrix}\right]$

A ₃₁ = 18 – 2 = 16, A ₃₂ = -(12 – 10) = -2, A ₃₃ = 2 – 15 = -13

De este modo, $Adj. A=\left[\begin{matrix}-33&3&16\\9&-2&-2\\26&0&-13\\\end{matrix}\right]$

X = A ^-1B

$X=\frac{1}{13}\left[\begin{matrix}-33&3&16\\9&-2&-2\\26&0&-13\\\end{matrix}\right]\left[\begin{matrix}50\\40\\60\\\end{matrix}\right]$

$\left[\begin{matrix}x\\y\\z\\\end{matrix}\right]=\frac{1}{13}\left[\begin{matrix}-33\times50+3\times40+16\times 60\\9\times 50-2\times 40-2\times 60\\26\times 50+0\times 40-13\times 60\\\end{matrix}\right]=\frac{1}{13}\left[\begin{matrix}-570\\250\\520\\\end{matrix}\right]=\left[\begin{matrix}-43.8\\19.2\\40\\\end{matrix}\right]$

x = 43,8, y = 19,2, z = 40