Complemento de un número con cualquier base b

Posted on by Rudeus Greyrat

b En esta publicación, se analiza un método general para encontrar el complemento con cualquier base arbitraria  .
Pasos para encontrar el complemento de (b-1) : Para encontrar el complemento de (b-1), 
 

  • Resta cada dígito del número del número más grande en el sistema numérico con base  b .
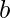  • Por ejemplo, si el número es un número de tres dígitos en base 9, resta el número de 888 ya que 8 es el número más grande en el sistema numérico de base 9.
  • El resultado obtenido es el complemento de (b-1) (complemento a 8).

Pasos para encontrar el complemento de b : Para encontrar el complemento de b, simplemente agregue 1 al complemento calculado (b-1).
Ahora, esto es cierto para cualquier base en el sistema numérico que existe. Se puede probar con bases familiares que es el complemento de 1 y 2.
Ejemplo : 
 

Let the number be 10111 base 2 (b=2)
Then, 1's complement will be 01000 (b-1)
2's complement will be 01001 (b)

Taking a number with Octal base:
Let the number be -456.
Then 7's complement will be 321
and 8's complement will be 322

A continuación se muestra la implementación de la idea anterior: 
 

C++

// CPP program to find complement of a
// number with any base b
#include<iostream>
#include<cmath>
 
using namespace std;
 
// Function to find (b-1)'s complement
int prevComplement(int n, int b)
{
    int maxDigit, maxNum = 0, digits = 0, num = n;
     
    // Calculate number of digits
    // in the given number
    while(n!=0)
    {
        digits++;
        n = n/10;
    }
     
    // Largest digit in the number
    // system with base b
    maxDigit = b-1;
     
    // Largest number in the number
    // system with base b
    while(digits--)
    {
        maxNum = maxNum*10 + maxDigit;
    }
     
    // return Complement
    return maxNum - num;
}
 
// Function to find b's complement
int complement(int n, int b)
{  
    // b's complement = (b-1)'s complement + 1
    return prevComplement(n,b) + 1;
}
 
// Driver code
int main()
{
    cout << prevComplement(25, 7)<<endl;
     
    cout << complement(25, 7);
     
    return 0;
}

Java

// Java program to find complement
// of a number with any base b
class GFG
{
 
// Function to find (b-1)'s complement
static int prevComplement(int n, int b)
{
    int maxDigit, maxNum = 0,
        digits = 0, num = n;
     
    // Calculate number of digits
    // in the given number
    while(n != 0)
    {
        digits++;
        n = n / 10;
    }
     
    // Largest digit in the number
    // system with base b
    maxDigit = b - 1;
     
    // Largest number in the number
    // system with base b
    while((digits--) > 0)
    {
        maxNum = maxNum * 10 + maxDigit;
    }
     
    // return Complement
    return maxNum - num;
}
 
// Function to find b's complement
static int complement(int n, int b)
{
    // b's complement = (b-1)'s
    // complement + 1
    return prevComplement(n, b) + 1;
}
 
// Driver code
public static void main(String args[])
{
    System.out.println(prevComplement(25, 7));
     
    System.out.println(complement(25, 7));
}
}
 
// This code is contributed
// by Kirti_Mangal

Python 3

# Python 3 program to find
# complement of a number
# with any base b
 
# Function to find
# (b-1)'s complement
def prevComplement(n, b) :
    maxNum, digits, num = 0, 0, n
 
    # Calculate number of digits
    # in the given number
    while n > 1 :
        digits += 1
        n = n // 10
 
    # Largest digit in the number
    # system with base b
    maxDigit = b - 1
 
    # Largest number in the number
    # system with base b
    while digits :
        maxNum = maxNum * 10 + maxDigit
        digits -= 1
         
    # return Complement
    return maxNum - num
 
# Function to find b's complement
def complement(n, b) :
 
    # b's complement = (b-1)'s
    # complement + 1
    return prevComplement(n, b) + 1
 
# Driver code
if __name__ == "__main__" :
     
    # Function calling
    print(prevComplement(25, 7))
    print(complement(25, 7))
 
# This code is contributed
# by ANKITRAI1

C#

// C# program to find complement
// of a number with any base b
class GFG
{
 
// Function to find (b-1)'s complement
static int prevComplement(int n, int b)
{
    int maxDigit, maxNum = 0,
        digits = 0, num = n;
     
    // Calculate number of digits
    // in the given number
    while(n != 0)
    {
        digits++;
        n = n / 10;
    }
     
    // Largest digit in the number
    // system with base b
    maxDigit = b - 1;
     
    // Largest number in the number
    // system with base b
    while((digits--) > 0)
    {
        maxNum = maxNum * 10 + maxDigit;
    }
     
    // return Complement
    return maxNum - num;
}
 
// Function to find b's complement
static int complement(int n, int b)
{
    // b's complement = (b-1)'s
    // complement + 1
    return prevComplement(n, b) + 1;
}
 
// Driver code
public static void Main()
{
    System.Console.WriteLine(prevComplement(25, 7));
     
    System.Console.WriteLine(complement(25, 7));
}
}
 
// This code is contributed
// by mits

PHP

<?php
// PHP program to find complement
// of a number with any base b
 
// Function to find (b-1)'s complement
function prevComplement($n, $b)
{
    $maxNum = 0;
    $digits = 0;
    $num = $n;
     
    // Calculate number of digits
    // in the given number
    while((int)$n != 0)
    {
        $digits++;
        $n = $n / 10;
    }
     
    // Largest digit in the number
    // system with base b
    $maxDigit = $b - 1;
     
    // Largest number in the number
    // system with base b
    while($digits--)
    {
        $maxNum = $maxNum * 10 +
                  $maxDigit;
    }
     
    // return Complement
    return $maxNum - $num;
}
 
// Function to find b's complement
function complement($n, $b)
{
    // b's complement = (b-1)'s
    // complement + 1
    return prevComplement($n, $b) + 1;
}
 
// Driver code
echo prevComplement(25, 7), "\n";
     
echo(complement(25, 7));
 
// This code is contributed
// by Smitha
?>

Javascript

<script>
 
// Javascript program to find complement
// of a number with any base b
 
// Function to find (b-1)'s complement
    function prevComplement(n , b) {
        var maxDigit, maxNum = 0, digits = 0,
        num = n;
 
        // Calculate number of digits
        // in the given number
        while (n != 0) {
            digits++;
            n = parseInt(n / 10);
        }
 
        // Largest digit in the number
        // system with base b
        maxDigit = b - 1;
 
        // Largest number in the number
        // system with base b
        while ((digits--) > 0) {
            maxNum = maxNum * 10 + maxDigit;
        }
 
        // return Complement
        return maxNum - num;
    }
 
    // Function to find b's complement
    function complement(n , b) {
        // b's complement = (b-1)'s
        // complement + 1
        return prevComplement(n, b) + 1;
    }
 
    // Driver code
     
        document.write(prevComplement(25, 7)+"<br/>");
 
        document.write(complement(25, 7));
 
// This code is contributed by todaysgaurav
 
</script>
Producción: 

41
42

 

Publicación traducida automáticamente

Artículo escrito por Ayusharma0698 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *