Los algoritmos Naive Bayes son un grupo de algoritmos de aprendizaje automático muy populares y comúnmente utilizados para la clasificación. Hay muchas formas diferentes de implementar el algoritmo Naive Bayes, como Gaussian Naive Bayes, Multinomial Naive Bayes, etc. Para obtener más información sobre los conceptos básicos de Naive Bayes, puede seguir este enlace.
Complement Naive Bayes es algo así como una adaptación del algoritmo Multinomial Naive Bayes estándar. Multinomial Naive Bayes no funciona muy bien en conjuntos de datos desequilibrados. Los conjuntos de datos desequilibrados son conjuntos de datos en los que la cantidad de ejemplos de alguna clase es mayor que la cantidad de ejemplos que pertenecen a otras clases. Esto significa que la distribución de ejemplos no es uniforme. Puede ser difícil trabajar con este tipo de conjunto de datos, ya que un modelo puede sobreajustar fácilmente estos datos a favor de la clase con más ejemplos.
Cómo funciona CNB:
Complement Naive Bayes es especialmente adecuado para trabajar con conjuntos de datos desequilibrados. En el complemento Naive Bayes, en lugar de calcular la probabilidad de que un elemento pertenezca a una determinada clase, calculamos la probabilidad de que el elemento pertenezca a todas las clases. Este es el significado literal de la palabra, complemento y por lo tanto se llama Complemento Naive Bayes.
Una descripción general paso a paso de alto nivel del algoritmo (sin ninguna matemática involucrada):
- Para cada clase, calcule la probabilidad de que la instancia dada no pertenezca a ella.
- Después del cálculo de todas las clases, verificamos todos los valores calculados y seleccionamos el valor más pequeño.
- Se selecciona el valor más pequeño (probabilidad más baja) porque es la probabilidad más baja de que NO sea esa clase en particular. Esto implica que tiene la mayor probabilidad de pertenecer realmente a esa clase. Entonces esta clase es seleccionada.
Nota: No seleccionamos el de mayor valor porque estamos calculando el complemento de la probabilidad. El que tiene el valor más alto es menos probable que sea la clase a la que pertenece ese elemento.
Ahora, consideremos un ejemplo: digamos, tenemos dos clases: Apples y Bananas y tenemos que clasificar si una oración dada está relacionada con apples o bananas, dada la frecuencia de un cierto número de palabras. Aquí hay una representación tabular del conjunto de datos simple:
| Número de oración | Redondo | Rojo | Largo | Amarillo | Suave | Clase |
| 1 | 2 | 1 | 1 | 0 | 0 | manzanas |
| 2 | 1 | 1 | 0 | 9 | 5 | plátanos |
| 3 | 2 | 1 | 0 | 0 | 1 | manzanas |
Recuento total de palabras en la clase ‘Manzanas’ = (2+1+1) + (2+1+1) = 8
Recuento total de palabras en la clase ‘Bananas’ = (1 + 1 + 9 + 5) = 16
Entonces, la probabilidad de que una oración pertenezca a la clase ‘manzanas’, ![]()
De manera similar, la probabilidad de que una oración pertenezca a la clase ‘Plátanos’,![]()
En la tabla anterior, hemos representado un conjunto de datos donde las columnas indican la frecuencia de las palabras en una oración determinada y luego muestran a qué clase pertenece la oración. Antes de comenzar, primero debe conocer el Teorema de Bayes . El Teorema de Bayes se usa para encontrar la probabilidad de un evento, dado que ocurre otro evento. La fórmula es:![]()
donde A y B son eventos, P(A) es la probabilidad de ocurrencia de A, y P(A|B) es la probabilidad de que ocurra A dado que el evento B ya ocurrió. P(B), la probabilidad de que ocurra el evento B no puede ser 0 porque ya ocurrió. Si desea obtener más información sobre Naive Bayes y el Teorema de Bayes, puede seguir este enlace.
Ahora veamos cómo funcionan Naive Bayes y Complement Naive Bayes. El algoritmo regular de Naive Bayes es,![]()
donde f i es la frecuencia de algún atributo. Por ejemplo, el número de veces que aparecen ciertas palabras en una oración.
Sin embargo, en complemento bayesiano ingenuo, la fórmula es:![]()
Si echa un vistazo más de cerca a las fórmulas, verá que el Naive Bayes complementario es justo lo contrario del Naive Bayes regular. En Naive Bayes, la clase con el mayor valor obtenido de la fórmula es la clase predicha. Entonces, dado que el Complemento Naive Bayes es justo lo contrario, la clase con el valor más pequeño obtenido de la fórmula CNB es la clase predicha.
Ahora, tomemos un ejemplo e intentemos predecirlo usando nuestro conjunto de datos y CNB,
| Redondo | Rojo | Largo | Amarillo | Suave | Clase |
| 1 | 1 | 0 | 0 | 1 | ? |
Entonces, necesitamos encontrar ![]()
y![]()
Necesitamos comparar ambos valores y seleccionar la clase como la clase predicha como la que tiene el valor más pequeño. Tenemos que hacer esto también para los plátanos y elegir el que tenga el valor más pequeño. es decir, si el valor de (y = Manzanas) es menor, la clase se predice como Manzanas, y si el valor de (y = Plátanos) es menor, la clase se predice como Plátanos.
Usando la fórmula Bayesiana ingenua del complemento para ambas clases,![]()
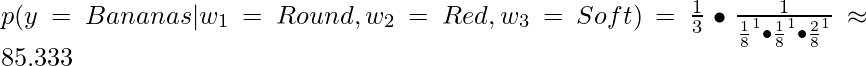
Ahora, dado que 6.302 < 85.333, la clase pronosticada es Manzanas .
NO usamos la clase con un valor más alto porque un valor más alto significa que es más probable que una oración con esas palabras NO pertenezca a la clase. Esta es exactamente la razón por la que este algoritmo se llama Complement Naive Bayes.
¿Cuándo usar CNB?
- Cuando el conjunto de datos está desequilibrado: si el conjunto de datos en el que se va a realizar la clasificación está desequilibrado, Multinomial y Gaussian Naive Bayes pueden dar una precisión baja. Sin embargo, Complement Naive Bayes funcionará bastante bien y proporcionará una precisión relativamente mayor.
- Para tareas de clasificación de texto: Complement Naive Bayes supera tanto a Gaussian Naive Bayes como a Multinomial Naive Bayes en tareas de clasificación de texto.
Implementación de CNB en Python:
para este ejemplo, usaremos el conjunto de datos de vino que está ligeramente desequilibrado. Determina el origen del vino a partir de diversos parámetros químicos. Para saber más sobre este conjunto de datos, puede consultar este enlace.
Para evaluar nuestro modelo, verificaremos la precisión del conjunto de prueba y el informe de clasificación del clasificador. Usaremos la biblioteca scikit-learn para implementar el algoritmo Complement Naive Bayes.
Código:
# Import required modules
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report
from sklearn.naive_bayes import ComplementNB
# Loading the dataset
dataset = load_wine()
X = dataset.data
y = dataset.target
# Splitting the data into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.15, random_state = 42)
# Creating and training the Complement Naive Bayes Classifier
classifier = ComplementNB()
classifier.fit(X_train, y_train)
# Evaluating the classifier
prediction = classifier.predict(X_test)
prediction_train = classifier.predict(X_train)
print(f"Training Set Accuracy : {accuracy_score(y_train, prediction_train) * 100} %\n")
print(f"Test Set Accuracy : {accuracy_score(y_test, prediction) * 100} % \n\n")
print(f"Classifier Report : \n\n {classification_report(y_test, prediction)}")
PRODUCCIÓN
Training Set Accuracy : 65.56291390728477 %
Test Set Accuracy : 66.66666666666666 %
Classifier Report :
precision recall f1-score support
0 0.64 1.00 0.78 9
1 0.67 0.73 0.70 11
2 1.00 0.14 0.25 7
accuracy 0.67 27
macro avg 0.77 0.62 0.58 27
weighted avg 0.75 0.67 0.61 27
Obtenemos una precisión del 65,56 % en el conjunto de entrenamiento y una precisión del 66,66 % en el conjunto de prueba. Son más o menos lo mismo y en realidad son bastante buenos dada la calidad del conjunto de datos. Este conjunto de datos es conocido por ser difícil de clasificar con clasificadores simples como el que hemos usado aquí. Así que la precisión es aceptable.
Conclusión:
ahora que sabe qué son los clasificadores de Complement Naive Bayes y cómo funcionan, la próxima vez que se encuentre con un conjunto de datos desequilibrado, puede intentar usar Complement Naive Bayes.
Referencias:
Publicación traducida automáticamente
Artículo escrito por alokesh985 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA