Las hipótesis son declaraciones sobre el problema dado. La prueba de hipótesis es un método estadístico que se utiliza para tomar una decisión estadística utilizando datos experimentales. La prueba de hipótesis es básicamente una suposición que hacemos sobre un parámetro de población. Evalúa dos afirmaciones mutuamente excluyentes sobre una población para determinar qué afirmación está mejor respaldada por los datos de muestra.
Ejemplo:
Usted dice que un estudiante promedio en la clase tiene 30 años o que un niño es más alto que las niñas. Todos esos son un ejemplo en el que asumimos o necesitamos alguna forma estadística para probarlos. Necesitamos alguna conclusión matemática, independientemente de lo que supongamos que es cierto.
Necesidad de la prueba de
hipótesis La prueba de hipótesis es un procedimiento importante en estadística. La prueba de hipótesis evalúa dos enunciados de población mutuamente excluyentes para determinar qué enunciado está más respaldado por datos de muestra. Cuando decimos que los hallazgos son estadísticamente significativos, es gracias a la prueba de hipótesis.
Parámetros de la prueba de hipótesis
- Hipótesis nula (H0): en estadística, la hipótesis nula es una declaración general dada o una posición predeterminada de que no existe relación entre dos casos medidos o ninguna relación entre grupos.
En otras palabras, es una suposición básica o hecha con base en el conocimiento del problema.
Ejemplo: la producción de una empresa es = 50 unidades/por día, etc. - Hipótesis alternativa (H1): La hipótesis alternativa es la hipótesis utilizada en la prueba de hipótesis que es contraria a la hipótesis nula.
Ejemplo: la producción de una empresa no es igual a 50 unidades por día, etc. - Nivel de significancia
Se refiere al grado de significación en el que aceptamos o rechazamos la hipótesis nula. No es posible obtener una precisión del 100 % para aceptar una hipótesis, por lo que seleccionamos un nivel de significación que suele ser del 5 %. Esto normalmente se denota con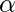 y, en general, es 0,05 o 5 %, lo que significa que su salida debe tener un 95 % de confianza para dar un tipo de resultado similar en cada muestra.
y, en general, es 0,05 o 5 %, lo que significa que su salida debe tener un 95 % de confianza para dar un tipo de resultado similar en cada muestra. - Valor
P El valor P, o probabilidad calculada, es la probabilidad de encontrar los resultados observados/extremos cuando la hipótesis nula (H0) de un problema de estudio dado es verdadera. Si su valor P es menor que el nivel de significancia elegido, entonces rechaza la hipótesis nula, es decir, acepta que su muestra afirma respaldar la hipótesis alternativa.
Ejemplo:
dada una moneda y no se sabe si es justa o engañosa, así que decidamos hipótesis nula y alternativa
- Hipótesis nula (H0): una moneda es una moneda justa.
- Hipótesis alternativa (H1): una moneda es una moneda engañosa.
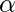 =
=
- Lance una moneda por primera vez y suponga que el resultado es cara- Valor P =
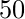 (ya que cara y cruz tienen la misma probabilidad)
(ya que cara y cruz tienen la misma probabilidad) - Lance una moneda por segunda vez y suponga que el resultado nuevamente es cara, ahora valor p =
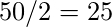
Ahora, arrojemos la moneda y calculemos el valor p (valor de probabilidad).
y de manera similar, lanzamos 6 veces consecutivas y obtuvimos el resultado como todas las caras, ahora valor P = ![]()
Pero establecemos nuestro nivel de significación como ![]() la tasa de error que permitimos y aquí vemos que estamos más allá de ese nivel, es decir, nuestra hipótesis nula no se cumple. por lo que debemos rechazar y proponer que esta moneda es una moneda engañosa que en realidad se debe a que nos da 6 caras consecutivas.
la tasa de error que permitimos y aquí vemos que estamos más allá de ese nivel, es decir, nuestra hipótesis nula no se cumple. por lo que debemos rechazar y proponer que esta moneda es una moneda engañosa que en realidad se debe a que nos da 6 caras consecutivas.
Error en la prueba de hipótesis
- Error tipo I: Cuando rechazamos la hipótesis nula, aunque esa hipótesis era verdadera. El error tipo I se denota por alfa.
- Errores tipo II: Cuando aceptamos la hipótesis nula pero es falsa. Los errores de tipo II se denotan por beta.
Publicación traducida automáticamente
Artículo escrito por deepanshu_jain y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA