Comprobar si el recuento de divisores pares de N es igual al recuento de divisores impares

Dado un entero positivo N , la tarea es comprobar si el recuento de divisores pares e impares de N es igual o no. Si son iguales, escriba «SÍ» , de lo contrario, escriba «NO» .
Ejemplos:

Entrada: N = 6
Salida: SI
Explicación:
El número 6 tiene cuatro factores:
1, 2, 3, 6,
conteo de divisores pares = 2 (2 y 6)
conteo de divisores impares = 2 (1 y 3)
Entrada: N = 9
Salida: NO
Explicación:
recuento de divisores pares = 0
recuento de divisores impares = 3 (1, 3 y 9)

Enfoque ingenuo: el enfoque ingenuo es encontrar todos los divisores del número dado y contar los divisores pares y los divisores impares y verificar si son iguales o no. Si son iguales, escriba «SÍ» , de lo contrario, escriba «NO» .
A continuación se muestra la implementación del enfoque anterior:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to check if count of even
// and odd divisors are equal
bool divisorsSame(int n)
{
    // To store the count of even
    // factors and odd factors
    int even_div = 0, odd_div = 0;
 
    // Loop till [1, sqrt(N)]
    for (int i = 1; i <= sqrt(n); i++) {
        if (n % i == 0) {
 
            // If divisors are equal
            // add only one
            if (n / i == i) {
 
                // Check for even
                // divisor
                if (i % 2 == 0) {
                    even_div++;
                }
 
                // Odd divisor
                else {
                    odd_div++;
                }
            }
 
            // Check for both divisor
            // i.e., i and N/i
            else {
 
                // Check if i is odd
                // or even
                if (i % 2 == 0) {
                    even_div++;
                }
                else {
                    odd_div++;
                }
 
                // Check if N/i is odd
                // or even
                if (n / i % 2 == 0) {
                    even_div++;
                }
                else {
                    odd_div++;
                }
            }
        }
    }
 
    // Return true if count of even_div
    // and odd_div are equals
    return (even_div == odd_div);
}
 
// Driver Code
int main()
{
    // Given Number
    int N = 6;
 
    // Function Call
    if (divisorsSame(N)) {
        cout << "Yes";
    }
    else {
        cout << "No";
    }
    return 0;
}

Java

// Java code for the above program
import java.util.*;
 
class GFG{
 
// Function to check if count of
// even and odd divisors are equal
static boolean divisorsSame(int n)
{
     
    // To store the count of even
    // factors and odd factors
    int even_div = 0, odd_div = 0;
 
    // Loop till [1, sqrt(N)]
    for(int i = 1; i <= Math.sqrt(n); i++)
    {
       if (n % i == 0)
       {
            
           // If divisors are equal
           // add only one
           if (n / i == i)
           {
                
               // Check for even
               // divisor
               if (i % 2 == 0)
               {
                   even_div++;
               }
                
               // Odd divisor
               else
               {
                   odd_div++;
               }
           }
            
           // Check for both divisor
           // i.e., i and N/i
           else
           {
                
               // Check if i is odd
               // or even
               if (i % 2 == 0)
               {
                   even_div++;
               }
               else
               {
                   odd_div++;
               }
                
               // Check if N/i is odd
               // or even
               if (n / i % 2 == 0)
               {
                   even_div++;
               }
               else
               {
                   odd_div++;
               }
           }
       }
    }
     
    // Return true if count of even_div
    // and odd_div are equals
    return (even_div == odd_div);
}
 
// Driver code
public static void main(String[] args)
{
    // Given number
    int N = 6;
 
    // Function call
    if (divisorsSame(N))
    {
        System.out.println("Yes");
    }
    else
    {
        System.out.println("No");
    }
}
}
 
// This code is contributed by offbeat

Python3

# Python3 program for the above approach
import math
 
# Function to check if count of even
# and odd divisors are equal
def divisorsSame(n):
 
    # To store the count of even
    # factors and odd factors
    even_div = 0; odd_div = 0;
 
    # Loop till [1, sqrt(N)]
    for i in range(1, int(math.sqrt(n))):
     
        if (n % i == 0):
 
            # If divisors are equal
            # add only one
            if (n // i == i):
 
                # Check for even
                # divisor
                if (i % 2 == 0):
                    even_div += 1;
                 
                # Odd divisor
                else:
                    odd_div += 1;
 
            # Check for both divisor
            # i.e., i and N/i
            else:
 
                # Check if i is odd
                # or even
                if (i % 2 == 0):
                    even_div += 1;
                 
                else:
                    odd_div += 1;
                 
                # Check if N/i is odd
                # or even
                if (n // (i % 2) == 0):
                    even_div += 1;
                 
                else:
                    odd_div += 1;
                 
    # Return true if count of even_div
    # and odd_div are equals
    return (even_div == odd_div);
 
# Driver Code
 
# Given Number
N = 6;
 
# Function Call
if (divisorsSame(N) == 0):
    print("Yes");
 
else:
    print("No");
 
# This code is contributed by Code_Mech

C#

// C# code for the above program
using System;
class GFG{
 
// Function to check if count of
// even and odd divisors are equal
static bool divisorsSame(int n)
{
     
    // To store the count of even
    // factors and odd factors
    int even_div = 0, odd_div = 0;
 
    // Loop till [1, sqrt(N)]
    for(int i = 1; i <= Math.Sqrt(n); i++)
    {
        if (n % i == 0)
        {
                 
            // If divisors are equal
            // add only one
            if (n / i == i)
            {
                     
                // Check for even
                // divisor
                if (i % 2 == 0)
                {
                    even_div++;
                }
                     
                // Odd divisor
                else
                {
                    odd_div++;
                }
            }
                 
            // Check for both divisor
            // i.e., i and N/i
            else
            {
                     
                // Check if i is odd
                // or even
                if (i % 2 == 0)
                {
                    even_div++;
                }
                else
                {
                    odd_div++;
                }
                     
                // Check if N/i is odd
                // or even
                if (n / i % 2 == 0)
                {
                    even_div++;
                }
                else
                {
                    odd_div++;
                }
            }
        }
    }
     
    // Return true if count of even_div
    // and odd_div are equals
    return (even_div == odd_div);
}
 
// Driver code
public static void Main()
{
    // Given number
    int N = 6;
 
    // Function call
    if (divisorsSame(N))
    {
        Console.Write("Yes");
    }
    else
    {
        Console.Write("No");
    }
}
}
 
// This code is contributed by Akanksha_Rai

Javascript

<script>
 
// JavaScript program for the above approach
 
// Function to check if count of even
// and odd divisors are equal
function divisorsSame(n)
{
    // To store the count of even
    // factors and odd factors
    let even_div = 0, odd_div = 0;
 
    // Loop till [1, sqrt(N)]
    for (let i = 1; i <= Math.sqrt(n); i++) {
        if (n % i == 0) {
 
            // If divisors are equal
            // add only one
            if (Math.floor(n / i) == i) {
 
                // Check for even
                // divisor
                if (i % 2 == 0) {
                    even_div++;
                }
 
                // Odd divisor
                else {
                    odd_div++;
                }
            }
 
            // Check for both divisor
            // i.e., i and N/i
            else {
 
                // Check if i is odd
                // or even
                if (i % 2 == 0) {
                    even_div++;
                }
                else {
                    odd_div++;
                }
 
                // Check if N/i is odd
                // or even
                if (Math.floor(n / i) % 2 == 0) {
                    even_div++;
                }
                else {
                    odd_div++;
                }
            }
        }
    }
 
    // Return true if count of even_div
    // and odd_div are equals
    return (even_div == odd_div);
}
 
// Driver Code
    // Given Number
    let N = 6;
 
    // Function Call
    if (divisorsSame(N)) {
        document.write("Yes");
    }
    else {
        document.write("No");
    }
 
// This code is contributed by Surbhi Tyagi.
 
</script>

Producción:

Yes

Complejidad Temporal: O(√N) , donde N es el número dado
Espacio Auxiliar: O(1)
Enfoque Eficiente: La idea es observar que los números cuya cuenta de divisores pares e impares son iguales forman la siguiente Progresión Aritmética :

2, 6, 10, 14, 18, 22, …

El K-ésimo término de la serie anterior es:
$K^{th} Term = 4*K + 2$
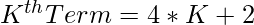
Ahora tenemos que comprobar si N es un término de la serie anterior o no mediante la ecuación:

=> $N = 4*K + 2$
=> $K = \frac{(N - 2)}{4}$

Si el valor de K calculado con la fórmula anterior es un número entero, entonces N es el número con el mismo número de divisores pares e impares.
De lo contrario , N no es el número con la misma cantidad de divisores pares e impares.

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to check if count of even
// and odd divisors are equal
bool divisorsSame(int n)
{
 
    // If (n-2)%4 is an integer, then
    // return true else return false
    return (n - 2) % 4 == 0;
}
 
// Driver Code
int main()
{
    // Given Number
    int N = 6;
 
    // Function Call
    if (divisorsSame(N)) {
        cout << "Yes";
    }
    else {
        cout << "No";
    }
    return 0;
}

Java

// Java code for the above program
import java.util.*;
 
class GFG{
     
// Function to check if count of
// even and odd divisors are equal
static boolean divisorsSame(int n)
{
     
    // If (n-2)%4 is an integer, then
    // return true else return false
    return (n - 2) % 4 == 0;
}
 
// Driver code
public static void main(String[] args)
{
     
    // Given number
    int N = 6;
 
    // Function call
    if (divisorsSame(N))
    {
        System.out.println("Yes");
    }
    else
    {
        System.out.println("No");
    }
    }
}
 
// This code is contributed by offbeat

Python3

# Python3 program for the above approach
 
# Function to check if count of even
# and odd divisors are equal
def divisorsSame(n):
 
    # If (n-2)%4 is an integer, then
    # return true else return false
    return (n - 2) % 4 == 0;
 
# Driver Code
 
# Given Number
N = 6;
 
# Function Call
if (divisorsSame(N)):
    print("Yes");
else:
    print("No");
 
# This code is contributed by Nidhi_biet

C#

// C# code for the above program
using System;
class GFG{
     
// Function to check if count of
// even and odd divisors are equal
static bool divisorsSame(int n)
{
     
    // If (n-2)%4 is an integer, then
    // return true else return false
    return (n - 2) % 4 == 0;
}
 
// Driver code
public static void Main()
{
     
    // Given number
    int N = 6;
 
    // Function call
    if (divisorsSame(N))
    {
        Console.Write("Yes");
    }
    else
    {
        Console.Write("No");
    }
    }
}
 
// This code is contributed by Code_Mech

Javascript

<script>
 
// javascript program for the above approach
 
// Function to check if count of even
// and odd divisors are equal
function divisorsSame( n)
{
 
    // If (n-2)%4 is an integer, then
    // return true else return false
    return (n - 2) % 4 == 0;
}
 
// Driver Code
 
    // Given Number
    let N = 6;
 
    // Function Call
    if (divisorsSame(N)) {
        document.write( "Yes");
    }
    else {
        document.write( "No");
    }
 
// This code contributed by gauravrajput1
 
</script>

Producción:

Yes

Complejidad temporal: O(1)
Espacio auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por spp____ y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta