Dados tres números N, S y X , la tarea es encontrar si es posible construir una secuencia A de longitud N , donde cada A[i] >= 0 para 1<=i<=N y la suma de todos los números en una secuencia es igual a S , y el XOR bit a bit de la secuencia es igual a X .
Ejemplos:
Entrada: N = 3, S = 10, X = 4
Salida: Sí
Explicación: Una de las secuencias posibles es {4, 3, 3} donde la suma es igual a 10 y XOR es igual a 4Entrada: N = 1, S = 5, X = 3
Salida: No
Enfoque: Consideremos los siguientes casos de prueba.
Caso-1: cuando N es igual a 1 , se puede ver fácilmente que cuando (S es igual a X) , solo devuelve » Sí «, de lo contrario, » No «.
Caso-2: Cuando N es mayor que igual a 3 , usa la fórmula (a + b) = (a xor b) + 2(a y b) Aquí se puede ver que (a + b) = S y (a xor b) = X por lo que la ecuación se convierte en S = X + 2(ab). Por lo tanto, (SX) debería ser par porque en el lado derecho tenemos 2(ab). Entonces, se puede decir que si S es impar, entonces X es impar y si S es par, entonces X es par, entonces (SX) también es par, lo que puede verificarse mediante (S%2 == X%2) también S >= X de lo contrario, AB se vuelve negativo, lo cual no es posible.
Caso-3: Para el caso N es igual a 3, es algo así como A + B + C = S y A^B^C = X. Usa la propiedad A^A = 0 y 0^A = A => X + ( S – X)/2 + (S – X)/2 = X + (SX) => X + ( S – X)/2 + (S – X)/2 = S y también así: X ^( ( S – X)/2 ^ (SX)/2 ) = X ^ 0 = X. Por lo tanto, se prueba que para N == 3 siempre habrá tal secuencia y podemos simplemente devolver “ Sí ”.
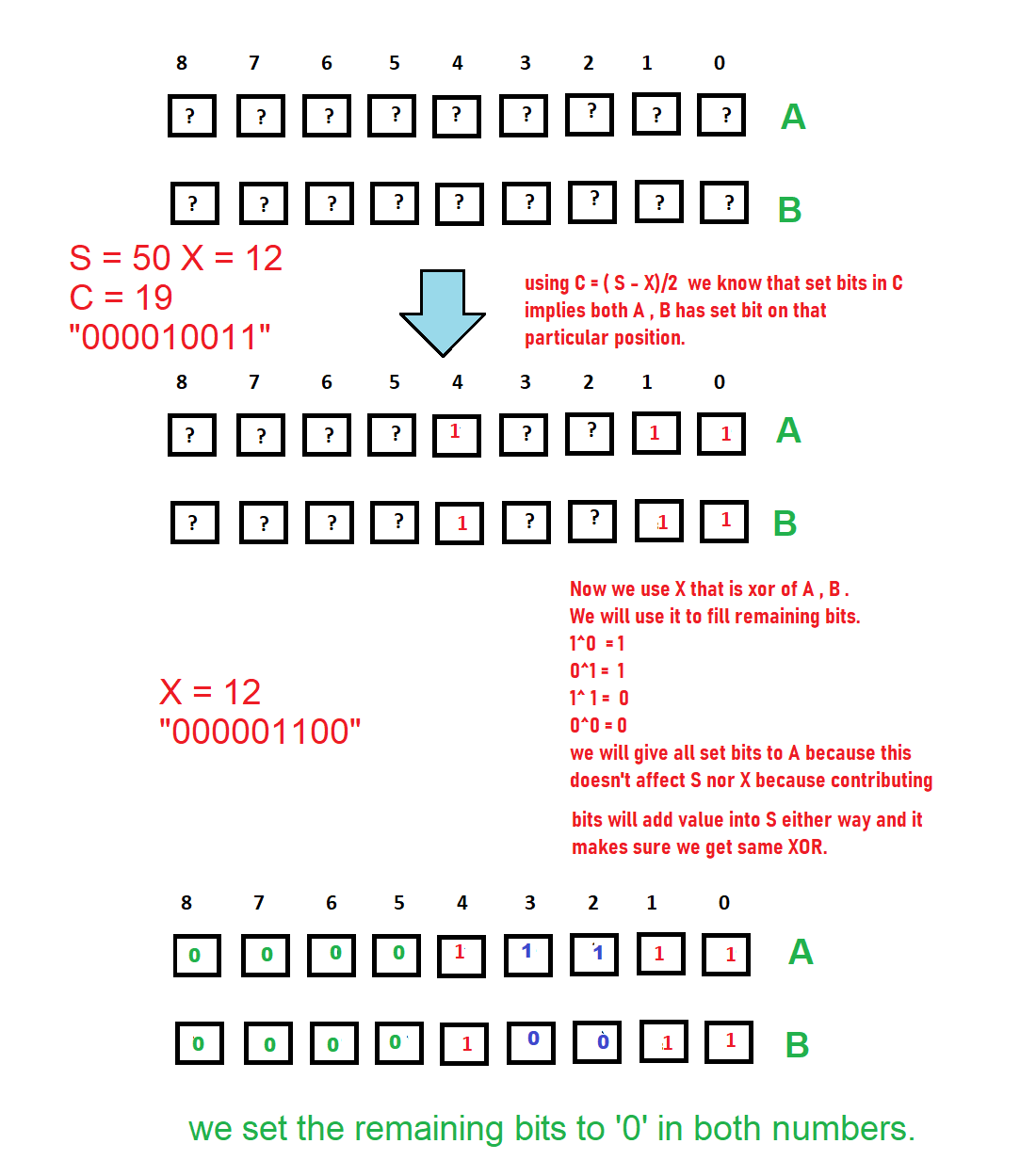
Caso-4: Cuando N == 2 y (S%2 == X%2) y S >= X , suponga que A + B == S y (A^B) == X entonces (A y B) == (SX)/2 De la ecuación discutida anteriormente. Sea C = AB Al observar detenidamente se puede notar que los bits de C son “1” sólo cuando los bits A y B son “1” para esa posición y apagados en caso contrario. Y X que es xor de A, B tiene un bit solo cuando hay diferentes bits que están en la i -ésima posición A tiene ‘0’ y B tiene ‘1’ o justo lo contrario: Así que mirando esta secuencia, asigne cada bit a variable A y B, C = ( S – X)/2. Asignar A y B desde C ->A = C, B = C
Ahora agregue la X en A o B para asignar todos los unos en A y todos los ceros en B , de modo que cuando hacemos XOR ambos números, los bits ‘1’ agregados en A serán opuestos a lo que agregamos en B que es ‘0’ . La parte divertida es cuando los bits establecidos de C coinciden con algunos bits establecidos de X, entonces no dará el xor deseado de X. Ahora, A = C+ X, B = C. Ahora A + B = ( C+ X) + C = S y cuando XOR AB es igual a X entonces se puede asegurar que existe tal par cuando A + B == S y (A^B) == X;
Siga los pasos a continuación para resolver el problema:
- Si S es mayor que igual a X, y S%2 es igual a X%2 , realice los siguientes pasos; de lo contrario, devuelva No.
- Si n es mayor que igual a 3, devuelva Sí.
- Si n es igual a 1, y si S es igual a X, entonces devuelve Sí , de lo contrario, devuelve No.
- Si n es igual a 2, inicialice la variable C como (SX)/2 y establezca las variables A y B como C y agregue el valor X a la variable A y si A^B es igual a X, entonces imprima Sí , de lo contrario imprima No.
A continuación se muestra la implementación del enfoque anterior.
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to find if any sequence is
// possible or not.
string findIfPossible(int N, int S, int X)
{
if (S >= X and S % 2 == X % 2) {
// Since, S is greater than equal to
// X, and either both are odd or even
// There always exists a sequence
if (N >= 3) {
return "Yes";
}
if (N == 1) {
// Only one case possible is
// S == X or NOT;
if (S == X) {
return "Yes";
}
else {
return "No";
}
}
// Considering the above conditions true,
// check if XOR of S^(S-X) is X or not
if (N == 2) {
int C = (S - X) / 2;
int A = C;
int B = C;
A = A + X;
if (((A ^ B) == X)) {
return "Yes";
}
else {
return "No";
}
}
}
else {
return "No";
}
}
// Driver Code
int main()
{
int N = 3, S = 10, X = 4;
cout << findIfPossible(N, S, X);
return 0;
}
C
// C program for the above approach
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
// Function to find if any sequence is
// possible or not.
char* findIfPossible(int N, int S, int X)
{
if (S >= X && S % 2 == X % 2) {
// Since, S is greater than equal to
// X, and either both are odd or even
// There always exists a sequence
if (N >= 3) {
return "Yes";
}
if (N == 1) {
// Only one case possible is
// S == X or NOT;
if (S == X) {
return "Yes";
}
else {
return "No";
}
}
// Considering the above conditions true,
// check if XOR of S^(S-X) is X or not
if (N == 2) {
int C = (S - X) / 2;
int A = C;
int B = C;
A = A + X;
if (((A ^ B) == X)) {
return "Yes";
}
else {
return "No";
}
}
}
else {
return "No";
}
}
// Driver Code
int main()
{
int N = 3, S = 10, X = 4;
printf("%s\n", findIfPossible(N, S, X));
return 0;
}
// This code is contributed by phalasi.
Java
// Java program for the above approach
import java.io.*;
import java.util.*;
class GFG {
// Function to find if any sequence is
// possible or not.
static void findIfPossible(int N, int S, int X)
{
if ((S >= X) && (S % 2 == X % 2)) {
// Since, S is greater than equal to
// X, and either both are odd or even
// There always exists a sequence
if (N >= 3) {
System.out.println("Yes");
}
if (N == 1) {
// Only one case possible is
// S == X or NOT;
if (S == X) {
System.out.println("Yes");
}
else {
System.out.println("No");
}
}
// Considering the above conditions true,
// check if XOR of S^(S-X) is X or not
if (N == 2) {
int C = (S - X) / 2;
int A = C;
int B = C;
A = A + X;
if (((A ^ B) == X)) {
System.out.println("Yes");
}
else {
System.out.println("No");
}
}
}
else {
System.out.println("No");
}
}
// Driver code
public static void main(String args[])
{
int N = 3, S = 10, X = 4;
findIfPossible(N, S, X);
}
}
// This code is contributed by code_hunt.
Python3
# Python program for the above approach # Function to find if any sequence is # possible or not. def findIfPossible(N, S, X): if (S >= X and S % 2 == X % 2): # Since, S is greater than equal to # X, and either both are odd or even # There always exists a sequence if (N >= 3): return "Yes" if (N == 1): # Only one case possible is # S == X or NOT if (S == X): return "Yes" else: return "No" # Considering the above conditions true, # check if XOR of S^(S-X) is X or not if (N == 2): C = (S - X) // 2 A = C B = C A = A + X if (((A ^ B) == X)): return "Yes" else: return "No" else: return "No" # Driver Code N = 3 S = 10 X = 4 print(findIfPossible(N, S, X)) # This code is contributed by shivanisinghss2110
C#
// C# program for the above approach
using System;
public class GFG {
// Function to find if any sequence is
// possible or not.
static void findIfPossible(int N, int S, int X)
{
if ((S >= X) && (S % 2 == X % 2)) {
// Since, S is greater than equal to
// X, and either both are odd or even
// There always exists a sequence
if (N >= 3) {
Console.WriteLine("Yes");
}
if (N == 1) {
// Only one case possible is
// S == X or NOT;
if (S == X) {
Console.WriteLine("Yes");
}
else {
Console.WriteLine("No");
}
}
// Considering the above conditions true,
// check if XOR of S^(S-X) is X or not
if (N == 2) {
int C = (S - X) / 2;
int A = C;
int B = C;
A = A + X;
if (((A ^ B) == X)) {
Console.WriteLine("Yes");
}
else {
Console.WriteLine("No");
}
}
}
else {
Console.WriteLine("No");
}
}
// Driver code
public static void Main(String[] args)
{
int N = 3, S = 10, X = 4;
findIfPossible(N, S, X);
}
}
// This code is contributed by Princi Singh
Javascript
<script>
// JavaScript Program to implement
// the above approach
// Function to find if any sequence is
// possible or not.
function findIfPossible(N, S, X) {
if (S >= X && S % 2 == X % 2) {
// Since, S is greater than equal to
// X, and either both are odd or even
// There always exists a sequence
if (N >= 3) {
return "Yes";
}
if (N == 1) {
// Only one case possible is
// S == X or NOT;
if (S == X) {
return "Yes";
}
else {
return "No";
}
}
// Considering the above conditions true,
// check if XOR of S^(S-X) is X or not
if (N == 2) {
let C = (S - X) / 2;
let A = C;
let B = C;
A = A + X;
if (((A ^ B) == X)) {
return "Yes";
}
else {
return "No";
}
}
}
else {
return "No";
}
}
// Driver Code
let N = 3, S = 10, X = 4;
document.write(findIfPossible(N, S, X));
// This code is contributed by Potta Lokesh
</script>
Yes
Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por omkartripathi y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA