Comprobar si las raíces de una ecuación cuadrática son recíprocas entre sí o no

Dados tres números A, B, C que representan los coeficientes (constantes) de una ecuación cuadrática  , la tarea es verificar si las raíces de la ecuación representada por estas constantes son recíprocas entre sí o no.
Ejemplos: 

Entrada: A = 2, B = -5, C = 2 
Salida: Sí 
Explicación: 
La ecuación cuadrática dada es  . 
Sus raíces son (1, 1/1) que son recíprocas entre sí.
Entrada: A = 1, B = -5, C = 6 
Salida: No 
Explicación: 
La ecuación cuadrática dada es  . 
Sus raíces son (2, 3) que no son recíprocas entre sí. 

Enfoque: La idea es utilizar el concepto de raíces cuadráticas para resolver el problema. Podemos formular la condición requerida para verificar si una raíz es el recíproco de la otra o no por:  

1. Sean las raíces de la ecuación 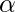 y  .
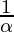2. El producto de las raíces de la ecuación anterior está dado por  *  .
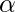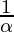3. Se sabe que el producto de las raíces es C/A. Por lo tanto, la condición requerida es C = A.

A continuación se muestra la implementación del enfoque anterior:  

// C++ program to check if roots
// of a Quadratic Equation are
// reciprocal of each other or not
 
#include <iostream>
using namespace std;
 
// Function to check if the roots
// of a quadratic equation are
// reciprocal of each other or not
void checkSolution(int a, int b, int c)
{
    if (a == c)
        cout << "Yes";
    else
        cout << "No";
}
 
// Driver code
int main()
{
    int a = 2, b = 0, c = 2;
 
    checkSolution(a, b, c);
 
    return 0;
}

// Java program to check if roots
// of a quadratic equation are
// reciprocal of each other or not
class GFG{
 
// Function to check if the roots 
// of a quadratic equation are
// reciprocal of each other or not
static void checkSolution(int a, int b, int c)
{
    if (a == c)
        System.out.print("Yes");
    else
        System.out.print("No");
}
 
// Driver code
public static void main(String[] args)
{
    int a = 2, b = 0, c = 2;
 
    checkSolution(a, b, c);
}
}
 
// This code is contributed by shubham

# Python3 program to check if roots
# of a Quadratic Equation are
# reciprocal of each other or not
 
# Function to check if the roots
# of a quadratic equation are
# reciprocal of each other or not
def checkSolution(a, b, c):
 
    if (a == c):
        print("Yes");
    else:
        print("No");
 
# Driver code
a = 2; b = 0; c = 2;
checkSolution(a, b, c);
 
# This code is contributed by Code_Mech

// C# program to check if roots
// of a quadratic equation are
// reciprocal of each other or not
using System;
class GFG{
 
// Function to check if the roots
// of a quadratic equation are
// reciprocal of each other or not
static void checkSolution(int a, int b, int c)
{
    if (a == c)
        Console.WriteLine("Yes");
    else
        Console.WriteLine("No");
}
 
// Driver code
public static void Main()
{
    int a = 2, b = 0, c = 2;
 
    checkSolution(a, b, c);
}
}
 
// This code is contributed by shivanisinghss2110

<script>
 
    // Javascript program to check if roots
    // of a Quadratic Equation are
    // reciprocal of each other or not
     
    // Function to check if the roots
    // of a quadratic equation are
    // reciprocal of each other or not
    function checkSolution(a, b, c)
    {
        if (a == c)
            document.write("Yes");
        else
            document.write("No");
    }
 
    let a = 2, b = 0, c = 2;
  
    checkSolution(a, b, c);
     
</script>

Yes

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)