Prerrequisito – Máquina de Turing
Las máquinas de Turing se pueden clasificar en términos generales en dos tipos, los aceptores y los transductores. Acceptor Turing Machine es un autómata utilizado para definir lenguajes aceptables para Turing. Tal máquina se puede usar para verificar si una string dada pertenece a un idioma o no. Se define como una máquina de 7 tuplas.
Llegando a los transductores: en general, los transductores son los dispositivos utilizados para convertir una forma de señal en otra. Lo mismo puede decirse de los transductores de la máquina de Turing.
Un transductor es un tipo de máquina de Turing que se utiliza para convertir la entrada dada en la salida después de que la máquina realiza varias lecturas y escrituras. No acepta ni rechaza una entrada, pero realiza una serie de operaciones para obtener la salida directamente en la misma cinta y se detiene cuando termina.
Algunos ejemplos de transductores de la Máquina de Turing son:
- Máquina de Turing para la adición
- Máquina de Turing para sustracción
- Máquina de Turing para la multiplicación
- Máquina de Turing para complemento a 1 y complemento a 2
Implementación:
Ahora propondremos un programa Java que fue escrito para simular la construcción y ejecución realizada por transductores de máquina de turing. Hay dos entradas que se deben dar mientras se ejecuta: un archivo .txt para definir el autómata (se da un ejemplo de máquina de multiplicación unaria después del código) y una string que se ingresará a través de la ventana de la consola que será la entrada en cinta para que el autómata la ejecute.
La ruta del archivo .txt debe proporcionarse como entrada. Esto se hizo para que el mismo programa se pueda usar para varios tipos de máquinas en lugar de codificar el autómata. Solo necesitamos escribir un archivo txt diferente para generar un autómata diferente.
Se eligió Java específicamente debido a la estructura OOP, mediante la cual se definió una clase para Estado, Transición, Máquina, etc., para poder encapsular varios aspectos de una entidad dentro de un objeto. Por ejemplo, una transición se define como una clase cuyos miembros son tres caracteres: leer, escribir y cambiar, que almacenan el símbolo de lectura, escriben un símbolo y cambian de dirección, respectivamente, junto con el índice del siguiente estado al que debe pasar la máquina. . Lo mismo se aplica a un objeto State, que almacena una lista de posibles transiciones salientes.
Ejemplo
Java
// Java Program to Illustrate Construction of Turing Machine
// Importing package
package turing_machine;
// Importing required classes
import java.io.File;
import java.io.FileNotFoundException;
import java.util.ArrayList;
import java.util.Scanner;
// Class 1
// Helper class
class Transition {
char read;
char write;
char shift;
int nextState;
// Constructor
// This divides string into specific symbols
// and next state's number
Transition(String s)
{
read = s.charAt(0);
write = s.charAt(2);
shift = s.charAt(4);
int l = s.length();
String substr = s.substring(6, l);
nextState = Integer.parseInt(substr);
}
}
// Class 2
// Helper class
class State {
// List of transitions for a state by
// creating ArrayList object of Transaction type
ArrayList<Transition> trs;
State(ArrayList<Transition> ts) { trs = ts; }
}
// Class 3
// Helper class
class Machine {
// Scanner object to read input
Scanner fs;
// Number of states to be read
int stateCount;
// Initialized to start state, and then to keep track
// of current state in automaton
int currState;
// To halt the machine when reached, must not contain
// any transitions
int finalState;
// Blank symbol defined for the machine in the input
// file
char blankSym;
// TAPE is a member of machine
StringBuffer Tape = new StringBuffer();
// List of states
ArrayList<State> states = new ArrayList<>();
// Method 1
void buildMachine(Scanner f)
{
this.fs = f;
// Printing the title in the first line of input
// file
System.out.println("\n\t" + readString());
// Reading the string of input symbols (space
// separated)
String s = readString();
System.out.println("Input symbols: " + s);
// Reading string of other tape symbols defined in
// transitions
s += " " + readString();
// Reading the blank symbol from the file
blankSym = readChar();
System.out.println("Blank symbol: " + blankSym);
s += " " + blankSym;
System.out.println("Tape symbols: " + s);
// Number of states to be defined, say N
stateCount = readInt();
System.out.println("\nNumber of States: "
+ stateCount);
// Current state variable (currState) is initialized
// to start-state
currState = readInt();
System.out.println("Start State: " + currState);
// addState() method is called N number of times
for (int i = 0; i < stateCount; i++)
addState(i);
}
// Method 2
void addState(int ind)
{
// number of transitions is read for a state and
// stored in trCount
int trCount = readInt();
// state with 0 transitions is assigned to be final
// state for the machine to halt
if (trCount == 0)
finalState = ind;
ArrayList<Transition> trs = new ArrayList<>();
for (int i = 0; i < trCount; i++) {
// Each transition object is created and
// appended to list
// of transitions
String s = readString();
Transition tr = new Transition(s);
trs.add(tr);
}
// new state object is created by passing list of
// transitions with the constructor
State st = new State(trs);
states.add(st);
}
// Method 3
// To read input from file object "fs" and return it
String readString()
{
String s = fs.next();
// To ignore lines starting from '//'
while (s.startsWith("//") || s.isEmpty())
s = fs.next();
return s;
}
// Method 4
// To read input from file object as string and
// return the first character
char readChar()
{
String s = fs.next();
while (s.startsWith("//") || s.isEmpty())
s = fs.next();
return s.charAt(0);
}
// Method 5
// To read input from file object and
// return it's integer form
int readInt()
{
String s = fs.next();
while (s.startsWith("//") || s.isEmpty())
s = fs.next();
return Integer.parseInt(s);
}
// Method 6
// To perform transitions on the tape starting from
// currState
void runTuring(int index) throws InterruptedException
{
while (currState != finalState) {
// Calling makeTrans() to perform transition and
// returning the index pointed by the R/W head
index = makeTrans(index);
if (index == -1)
throw new InterruptedException(
"ERROR: Transition Not Found! Machine HALTED.");
// Tape instance printed after each transition
printTape(index);
}
}
int makeTrans(int index) throws InterruptedException
{
if (Tape.charAt(index) == '$')
throw new InterruptedException(
"ERROR: Head left the Tape boundary! Machine HALTED.");
State st = states.get(currState);
// to traverse across the list of transitions to
// match tape symbol with read symbol
for (Transition tr : st.trs) {
if (tr.read == Tape.charAt(index)) {
// to write the write-symbol onto the tape
Tape.replace(index, index + 1,
String.valueOf(tr.write));
currState = tr.nextState;
switch (tr.shift) {
case 'R':
return index + 1; // shift right on tape
case 'L':
return index - 1; // shift left on tape
default:
return -1; // unknown shift symbol
}
}
}
return -1; // transition not found
}
void printTape(int index)
{
int interval = 500; // in milliseconds
System.out.println("Tape: " + Tape);
for (int i = 0; i < index; i++)
System.out.print(" "); // to align
// to print the R/W head of machine pointing to
// particular tape index along with current state
// index
System.out.println(" ^q" + currState + "\n");
try {
// to print new instance of tape with a
// particular interval
Thread.sleep(interval);
}
catch (InterruptedException e) {
System.out.println(e.getMessage());
}
}
}
// Class 4
// Helper class
class FileScanner {
Scanner scan = new Scanner(System.in);
Scanner fileScan;
String inputstr;
FileScanner() throws FileNotFoundException
{
// to read the input from .txt file
System.out.print("Enter file path: ");
String path = scan.nextLine();
fileScan = new Scanner(new File(path));
fileScan.useDelimiter("\n");
}
String buildTape(String str, char blank)
{
// str is the input string to be added to the tape
// tape defined to begin and end with '$' symbol to
// avoid indefinite transitions
String s = "$"; // begin
for (int i = 0; i < 5; i++)
s += blank; // adding few blank symbols
s = s.concat(str); // adding the input string
for (int i = 0; i < 30; i++)
s += blank; // adding few more blanks
s += '$'; // end
// this concatenated string forms a Tape and is
// returned
return s;
}
void setTape(Machine m)
{
// read input string from console
System.out.print("\nEnter input string: ");
inputstr = scan.nextLine();
// pass string as parameter to buildTape() method
m.Tape = new StringBuffer(
buildTape(inputstr, m.blankSym));
// 6 == initial index of tape that is pointed by R/W
// head
m.printTape(6);
}
}
// Class 5
// Main class
public class TuringMain {
// Main driver method
public static void main(String[] args)
{
// Display message for better readability
System.out.println(
"\n\tTRANSDUCER TURING MACHINE BUILDER\n");
// Creating new object of Machine class
Machine m = new Machine();
// Try block to check for exceptions
try {
FileScanner fileScanner = new FileScanner();
// constructing the machine using details from
// Scanner object that reads the file
m.buildMachine(fileScanner.fileScan);
fileScanner.setTape(
m); // setting tape for the machine
m.runTuring(
6); // to start execution of Turing Machine
}
catch (FileNotFoundException
| InterruptedException e) {
System.out.println(e);
System.exit(0);
}
}
}
El archivo de entrada que define símbolos, estados y transiciones para Automaton for Unary multiplication :
//las líneas que comienzan con ‘//’ son ignoradas por el programa durante la lectura para que el texto de entrada pueda ser comentado
//título, se imprimirá en la consola
MAQUINA PARA MULTIPLICACION UNARIA
// símbolos de entrada: 1 para definir un número unario, 0 como delimitador
0 1
//símbolos de cinta – distintos a las entradas
Y
//símbolo en blanco
B
//número de estados
8
// estado de inicio
0
//transiciones
//formato – leer,escribir,cambiar,siguiente estado
//para el estado q0, se leerán 2 transiciones para este estado
2
1 HAB 1
0 habitaciones 6
//estado q1
2
0 0 R 2
1 1 R 1
//estado q2
2
0 0 L 5
1 AÑO 3
//estado q3
3
0 0 R 3
1 1 R 3
B 1 L 4
//estado q4
3
0 0 L 4
1 1 L 4
AÑO 2
//estado q5
4
0 0 L 5
1 1 L 5
Y 1 L 5
BBR 0
//estado q6
2
1 HAB 6
0 habitaciones 7
// estado q7: la máquina se detiene cuando alcanza este estado ya que se definen 0 transiciones
0
La entrada de texto para Turing Machine para copiar datos se proporciona en ENLACE .
Nota: El programa debe ejecutarse en una máquina local o en un IDE que acepte rutas para archivos de E/S.
A continuación se muestra cómo se ve la SALIDA para el autómata de multiplicación unaria con «1101110» como entrada (unaria 2 * unaria 3):
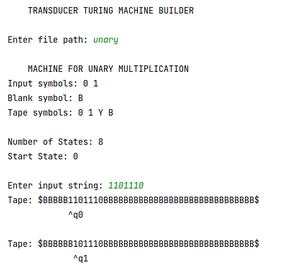
Primera parte de la salida, cuando la máquina comienza a ejecutar en la cinta.
(después de varias iteraciones)

Después de imprimir todas las instancias de la cinta en intervalos, la máquina alcanza el estado final y se detiene. Podemos ver que se obtuvo «111111» o unario-6 para la entrada 2*3.
Con un poco de esfuerzo, el mismo programa puede extenderse para que también funcione con máquinas de Turing de tipo aceptador. Se anima a cualquier persona interesada a mejorar el artículo.
Publicación traducida automáticamente
Artículo escrito por tarunsrivatsa17 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA