Construyendo un gráfico no dirigido y encontrando la ruta más corta usando Diccionarios en Python

requisitos previos: 

• BFS para un gráfico
• Diccionarios en Python

En este artículo, veremos cómo construir un gráfico no dirigido y luego encontrar la ruta más corta entre dos Nodes/vértices de ese gráfico fácilmente usando diccionarios en lenguaje Python. 

Construyendo un gráfico usando diccionarios

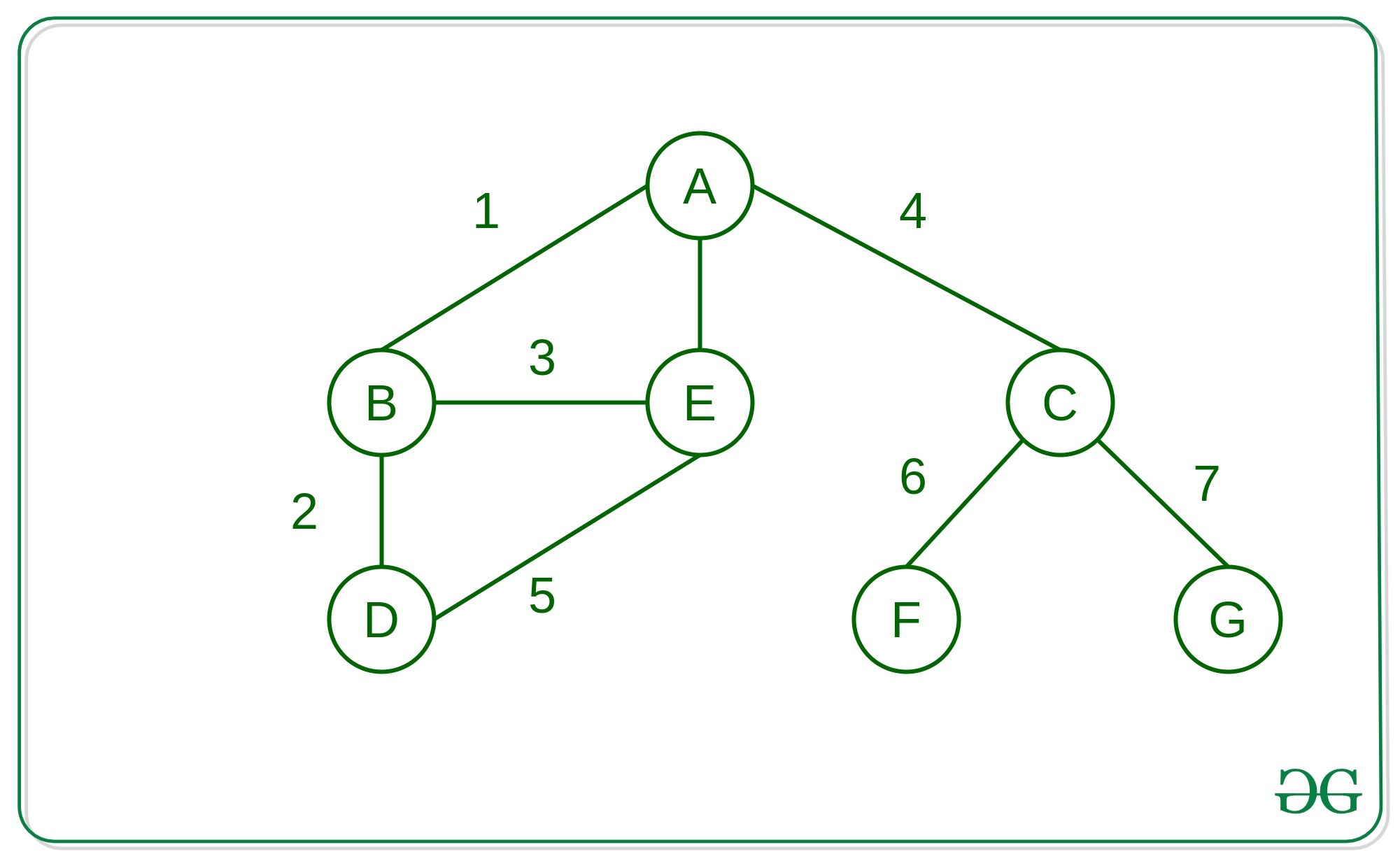
Enfoque: la idea es almacenar la lista de adyacencia en los diccionarios, lo que ayuda a almacenar el gráfico en cualquier formato, no solo en forma de números enteros. Aquí hemos utilizado caracteres como referencia en aquellos lugares en los que también se pueden utilizar objetos personalizados.

A continuación se muestra la implementación del enfoque anterior:  

# Python3 implementation to build a
# graph using Dictionaries
 
from collections import defaultdict
 
# Function to build the graph
def build_graph():
    edges = [
        ["A", "B"], ["A", "E"],
        ["A", "C"], ["B", "D"],
        ["B", "E"], ["C", "F"],
        ["C", "G"], ["D", "E"]
    ]
    graph = defaultdict(list)
     
    # Loop to iterate over every
    # edge of the graph
    for edge in edges:
        a, b = edge[0], edge[1]
         
        # Creating the graph
        # as adjacency list
        graph[a].append(b)
        graph[b].append(a)
    return graph
 
if __name__ == "__main__":
    graph = build_graph()
     
    print(graph)

{
   'G': ['C'], 
   'F': ['C'], 
   'E': ['A', 'B', 'D'], 
   'A': ['B', 'E', 'C'], 
   'B': ['A', 'D', 'E'], 
   'D': ['B', 'E'], 
   'C': ['A', 'F', 'G']
}

Ruta más corta entre dos Nodes de gráfico

Enfoque: la idea es usar la cola y visitar cada Node adyacente de los Nodes iniciales que atraviesan el gráfico en forma de búsqueda en amplitud para encontrar el camino más corto entre dos Nodes del gráfico.

A continuación se muestra la implementación del enfoque anterior:

# Python implementation to find the
# shortest path in the graph using
# dictionaries
 
# Function to find the shortest
# path between two nodes of a graph
def BFS_SP(graph, start, goal):
    explored = []
     
    # Queue for traversing the
    # graph in the BFS
    queue = [[start]]
     
    # If the desired node is
    # reached
    if start == goal:
        print("Same Node")
        return
     
    # Loop to traverse the graph
    # with the help of the queue
    while queue:
        path = queue.pop(0)
        node = path[-1]
         
        # Condition to check if the
        # current node is not visited
        if node not in explored:
            neighbours = graph[node]
             
            # Loop to iterate over the
            # neighbours of the node
            for neighbour in neighbours:
                new_path = list(path)
                new_path.append(neighbour)
                queue.append(new_path)
                 
                # Condition to check if the
                # neighbour node is the goal
                if neighbour == goal:
                    print("Shortest path = ", *new_path)
                    return
            explored.append(node)
 
    # Condition when the nodes
    # are not connected
    print("So sorry, but a connecting"\
                "path doesn't exist :(")
    return
 
# Driver Code
if __name__ == "__main__":
     
    # Graph using dictionaries
    graph = {'A': ['B', 'E', 'C'],
            'B': ['A', 'D', 'E'],
            'C': ['A', 'F', 'G'],
            'D': ['B', 'E'],
            'E': ['A', 'B', 'D'],
            'F': ['C'],
            'G': ['C']}
     
    # Function Call
    BFS_SP(graph, 'A', 'D')

Shortest path =  A B D